《概率论与数理逻辑》-期末习题复习

滴啦嘟啦哒

已于 2024-01-03 17:18:07 修改

阅读量2.3k

点赞数 44

分类专栏：期末复习文章标签：概率论

于 2023-12-28 17:32:35 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/m0_75114363/article/details/135251093

版权

期末复习专栏收录该内容

6 篇文章

订阅专栏

目录

第一章：随机变量及其概率

考点1.由四大公式求概率

知识铺垫：

题目1描述：

解题思路：

题目2描述：

解题思路：

题目3描述：

解题思路：

题目4描述：

解题思路：

考点2.古典概型求概率

知识铺垫：

题目描述：

解题思路：

考点3.全概率公式和贝叶斯公式

知识铺垫：

题目1描述：

解题思路：

题目2描述：

解题思路：

考点4.伯努利模型求概率

知识铺垫：

题目描述：

解题思路：

第二章：一位随机变量及其分布

考点1.离散型随机变量求分布律

知识铺垫：

题目描述：

解题思路：

考点2.利用常见的离散型分布求概率

知识铺垫：

题目描述：

解题思路：

考点3.连续型分布的相关计算

知识铺垫：

题目1描述：

解题思路：

题目2描述：

解题思路：

题目3描述：

解题思路：

考点4.利用常见的连续型分布模型进行计算

知识铺垫：

题目1描述：

解题思路：

题目2描述：

解题思路：

考点5.离散型变量x的函数分布

知识铺垫：

题目描述：

解题思路：

考点6.连续型变量x的函数分布

知识铺垫：

题目描述：

解题思路：

第三章：二维随机变量及其分布

考点1.二维离散型随机变量的分布

知识铺垫：

题目描述：

解题思路：

考点2.二维连续型随机变量的分布

知识铺垫：

题目描述：

解题思路：

第四章：随机变量的数学特征

考点1.常见分布的数学特征

知识铺垫：

题目1描述：

解题思路：

题目2描述：

解题思路：

考点2.离散型随机变量的协方差、相关系数

知识铺垫：

题目描述：

解题思路：

考点3.连续型随机变量的协方差、相关系数

知识铺垫：

题目描述：

解题思路：

第五、六章：大数定理、中心极限定理、数理统计基本概念

考点1.大数定律

知识铺垫：

题目描述：

解题思路：

考点2.中心极限定理

知识铺垫：

题目1描述：

解题思路：

题目2描述：

解题思路：

考点3.三个重要分布

知识铺垫：

题目1描述：

解题思路：

题目2描述：

解题思路：

第七章：参数估计

考点1.未知参数的矩估计和极大似然估计

知识铺垫：

题目描述：

解题思路：

考点2.估计量的无偏性和有效性

知识铺垫：

题目描述：

解题思路：

考点3.未知参数的区间估计

知识铺垫：

题目描述：

解题思路：

第八章：假设检验

考点1.正态总体下均值的假设检验

知识铺垫：

题目描述：

解题思路：

考点2.正态总体下方差的检验

知识铺垫：

题目描述：

解题思路：

考点：线性回归

题目描述：

前言

最近开始了概率论的期末复习，本篇文章理论上来说可以应对大多数学校的期末考试。仅作学习分享，如有谬误欢迎指正。

本篇文章树状图框架可自取（.xmind文件）：HolasRep: Hola的资料分享仓库！

本篇文章主要参考资料如下：

b站框框老师的网课：第一章：随机事件及其概率（一）_哔哩哔哩_bilibili

12.28初版：第五章过后的知识铺垫处待补充解释；类似题还未更新；大数定理部分还没有什么题；期末考试前会持续更新。

12.28晚更，更新了大部分解释，剩余工作以补充习题为主。

第一章：随机变量及其概率

考点1.由四大公式求概率

知识铺垫：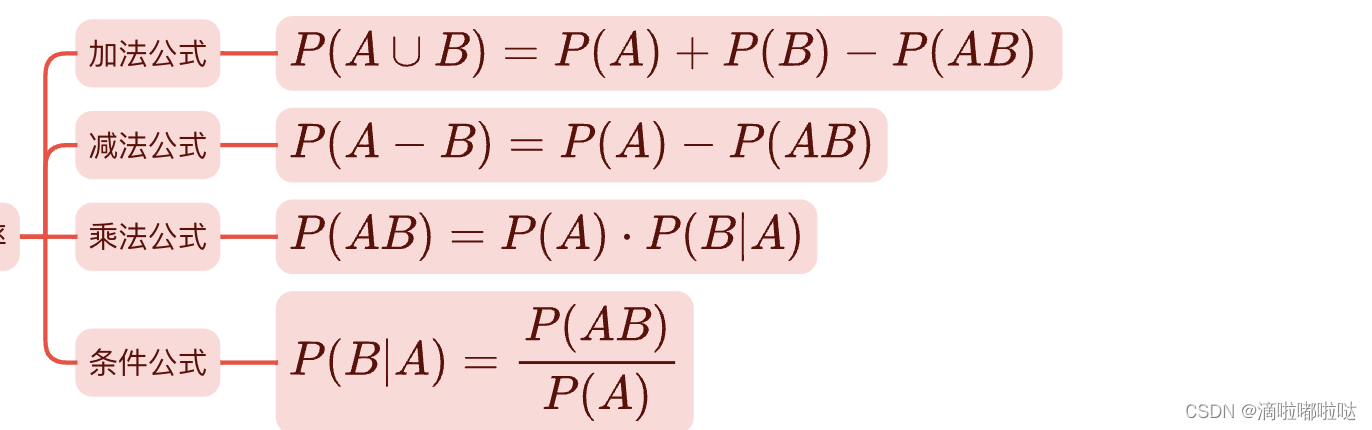

总结：

记住四个公式的基本形式，在做题时灵活运用即可

题目1描述：

解题思路：

🌟 $ABC \subset AB$ ,则P(ABC) $\leq$ P(AB)

类似题：

题目2描述：

解题思路：

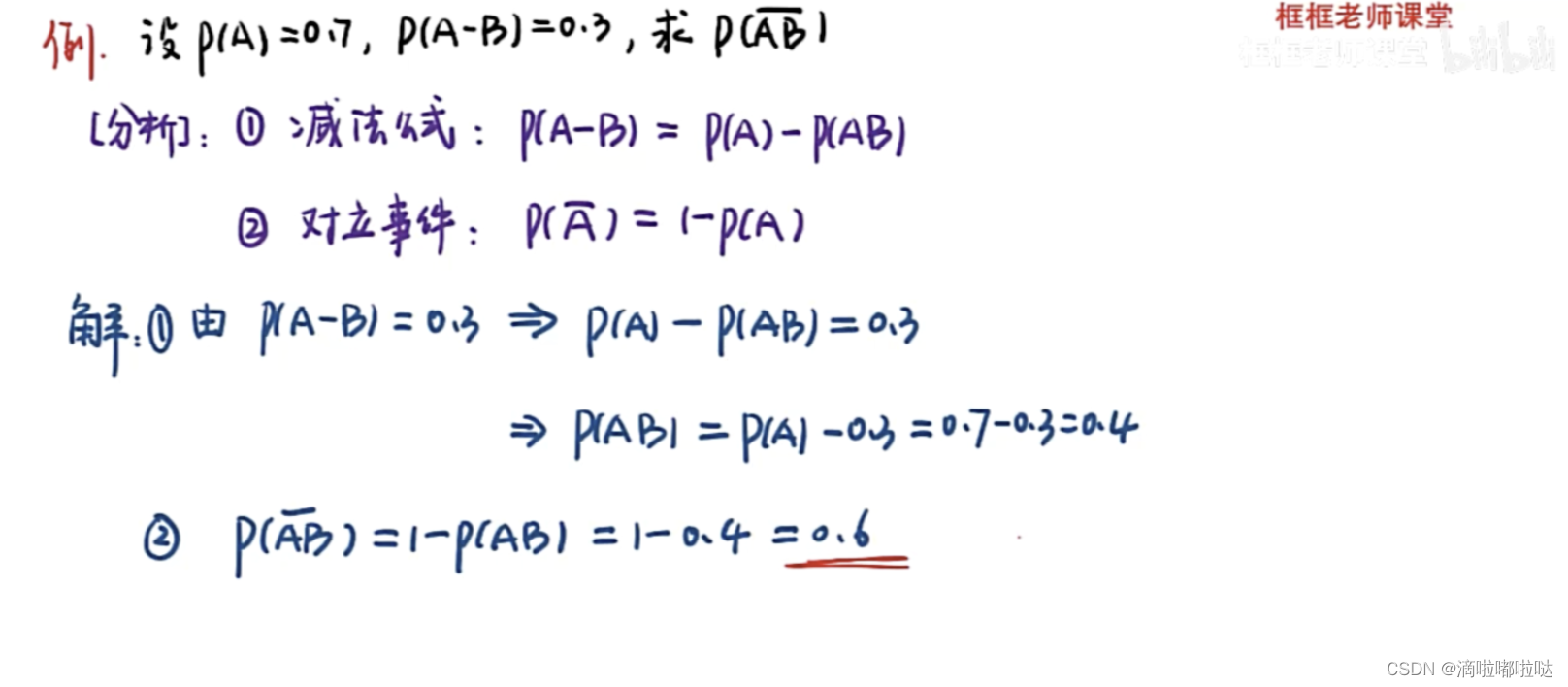
🌟在做题时，将 P(A-B) 化为 P(A) - P(AB) 是常常会用到的操作。

类似题：

题目3描述：

解题思路：

🌟 $P(A \overline B) = P(A·(1-B)) = P(A-B) = P(A) - P(AB)$

类似题：

题目4描述：

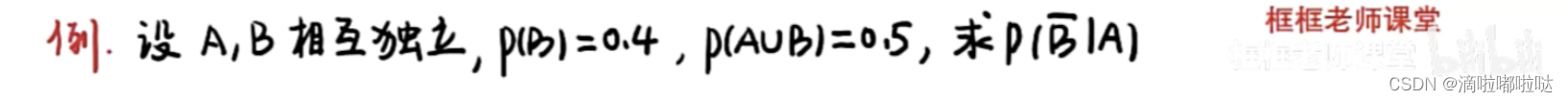
解题思路：

🌟若两事件相互独立，则两事件的条件概率与原来没有变化

类似题：

解答：

核心在于减法公式的使用

考点2.古典概型求概率

知识铺垫：

其实就是高中的知识，没啥好说的

总结：

题目描述：

解题思路：

🌟古典概型的两个特点：有有限个基本事件；每个基本事件发生的可能性相等

类似题：

考点3.全概率公式和贝叶斯公式

知识铺垫：

总结：

全概率用来以小算大，贝叶斯用来以大算小

题目1描述：

解题思路：

up主给出的做题步骤值得借鉴

类似题：

题目2描述：

解题思路：

类似题：

解答：

强烈建议所有的题都要自己写一遍，不要认为答案对了就够了，还要追求表述的规范性。

考点4.伯努利模型求概率

知识铺垫：

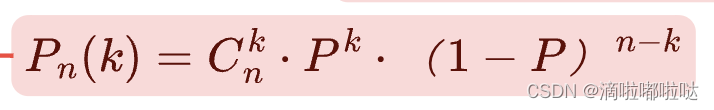
总结：

记住公式就行，实际靠高中知识就能解决

题目描述：

解题思路：

🌟记住计算公式就行

类似题：

第二章：一位随机变量及其分布

考点1.离散型随机变量求分布律

知识铺垫：

要明白分布律是怎么画的

总结：

题目描述：

解题思路：

类似题：

解答：

注意表述规范

考点2.利用常见的离散型分布求概率

知识铺垫：

常见离散型分布：

总结：

0-1，二项，超几何都异曲同工，注意一下几何分布和泊松分布。

题目描述：

解题思路：

🌟此题为二项分布，注意计算公式即可

类似题：

解答：

1.二项分布近似为泊松分布

2.注意思路，采用对立事件的方法来计算

考点3.连续型分布的相关计算

知识铺垫：

搞清楚概率密度函数和分布函数的定义

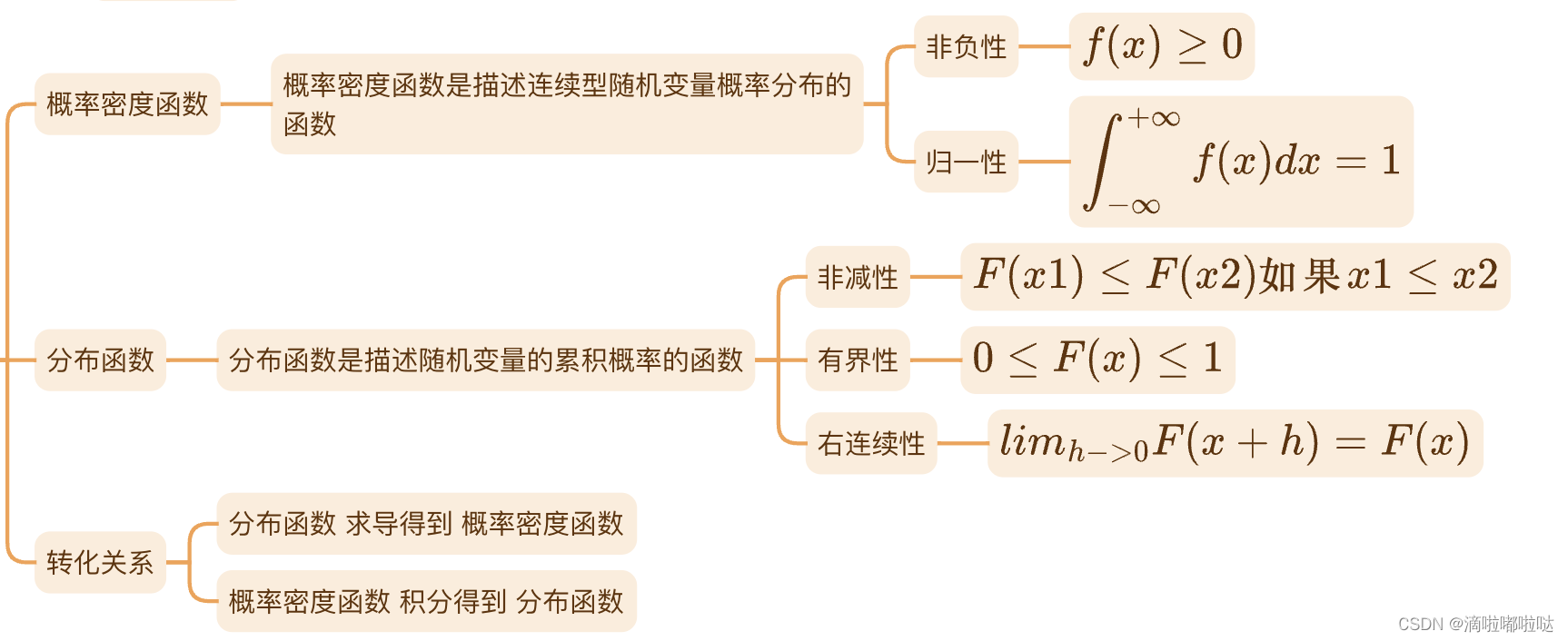
总结：

题目1描述：

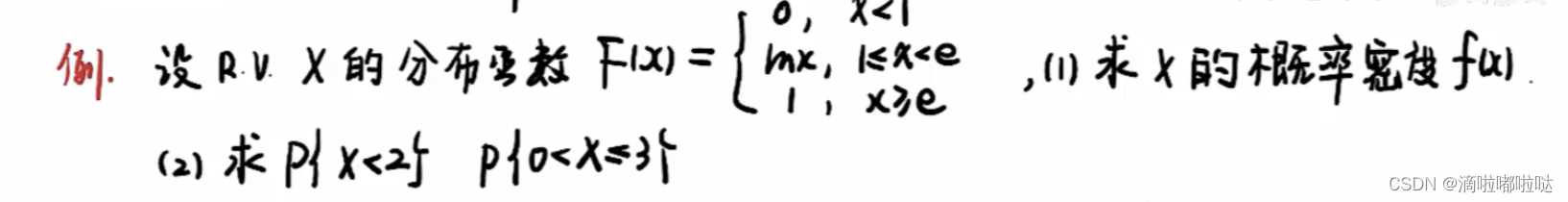
解题思路：

🌟

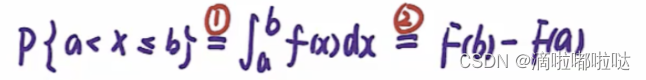
类似题：

题目2描述：

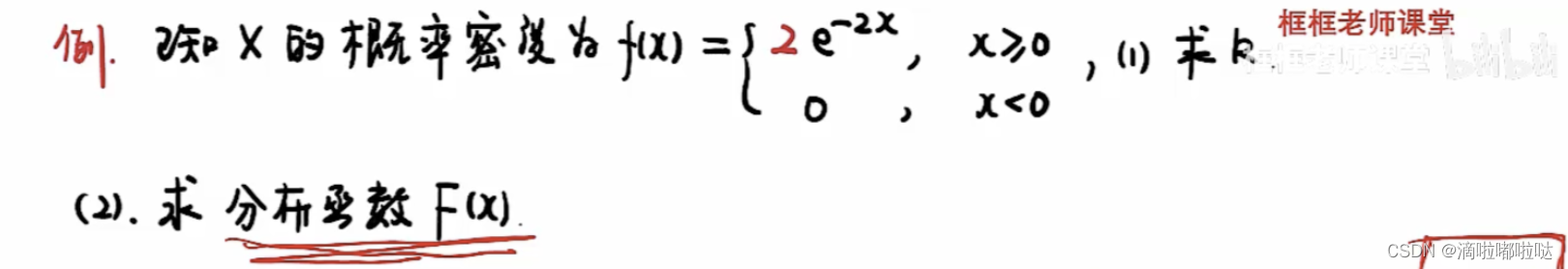
解题思路：

🌟1.概率密度函数具有归一性 2.概率密度函数积分得到分布函数 3.注意严谨性，不定积分后是带常数的，还需要进一步计算

类似题：

题目3描述：

解题思路：

🌟 $F(-\infty) = 0;F(+\infty) = 1$

类似题：

考点4.利用常见的连续型分布模型进行计算

知识铺垫：

常见连续型分布：

总结：

这三种分布的分布函数和概率密度函数都需要记，之后会给出常见分布的相关函数的总结。

题目1描述：

解题思路：

🌟

类似题：

题目2描述：

解题思路：

🌟1.注意正态分布的概率密度函数 2.注意正态分布的标准化方法 3. $\Phi_0(0) = 0.5$

类似题：

考点5.离散型变量x的函数分布

知识铺垫：

这类题很简单，先求取值再求概率即可。

总结：

题目描述：

解题思路：

🌟先求取值，再求概率

类似题：

类似题：

考点6.连续型变量x的函数分布

知识铺垫：

给出常见分布的相关函数

总结：

题目描述：

解题思路：

🌟核心：

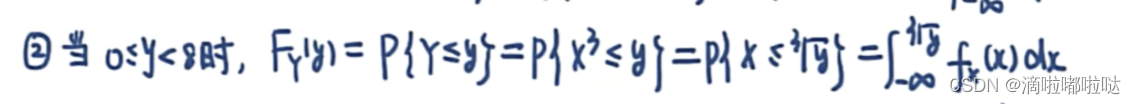
类似题：

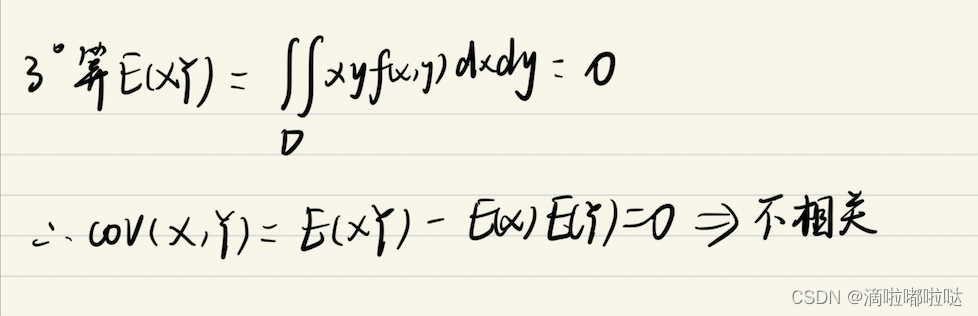
类似题：

类似题：

第三章：二维随机变量及其分布

考点1.二维离散型随机变量的分布

知识铺垫：

离散型变量的联合、边缘分布律、题哦啊见分布律、独立是很好理解的，根据分布律表格就可以全部解决，具体方法看下面的题就行。

总结：

题目描述：

解题思路：

类似题：

考点2.二维连续型随机变量的分布

知识铺垫：

总结：

看上图即可。

题目描述：

解题思路：

类似题：

类似题：

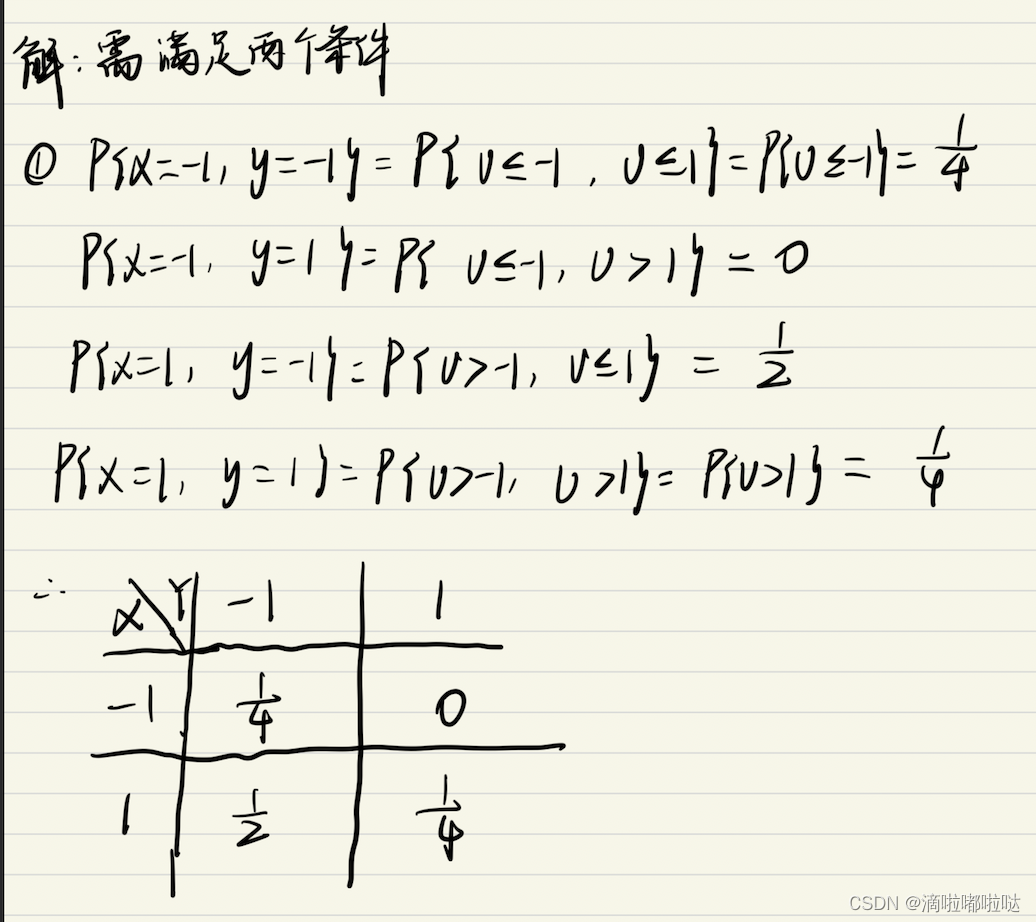
第四章：随机变量的数学特征

考点1.常见分布的数学特征

知识铺垫：

总结：

记下来就好。

题目1描述：

解题思路：

🌟 并且注意，-2x应该视作+（-2x）

类似题：

题目2描述：

解题思路：

🌟 $D(X) = E(X^2)-E(X)^2$

类似题：

考点2.离散型随机变量的协方差、相关系数

知识铺垫：

总结：

题目描述：

解题思路：

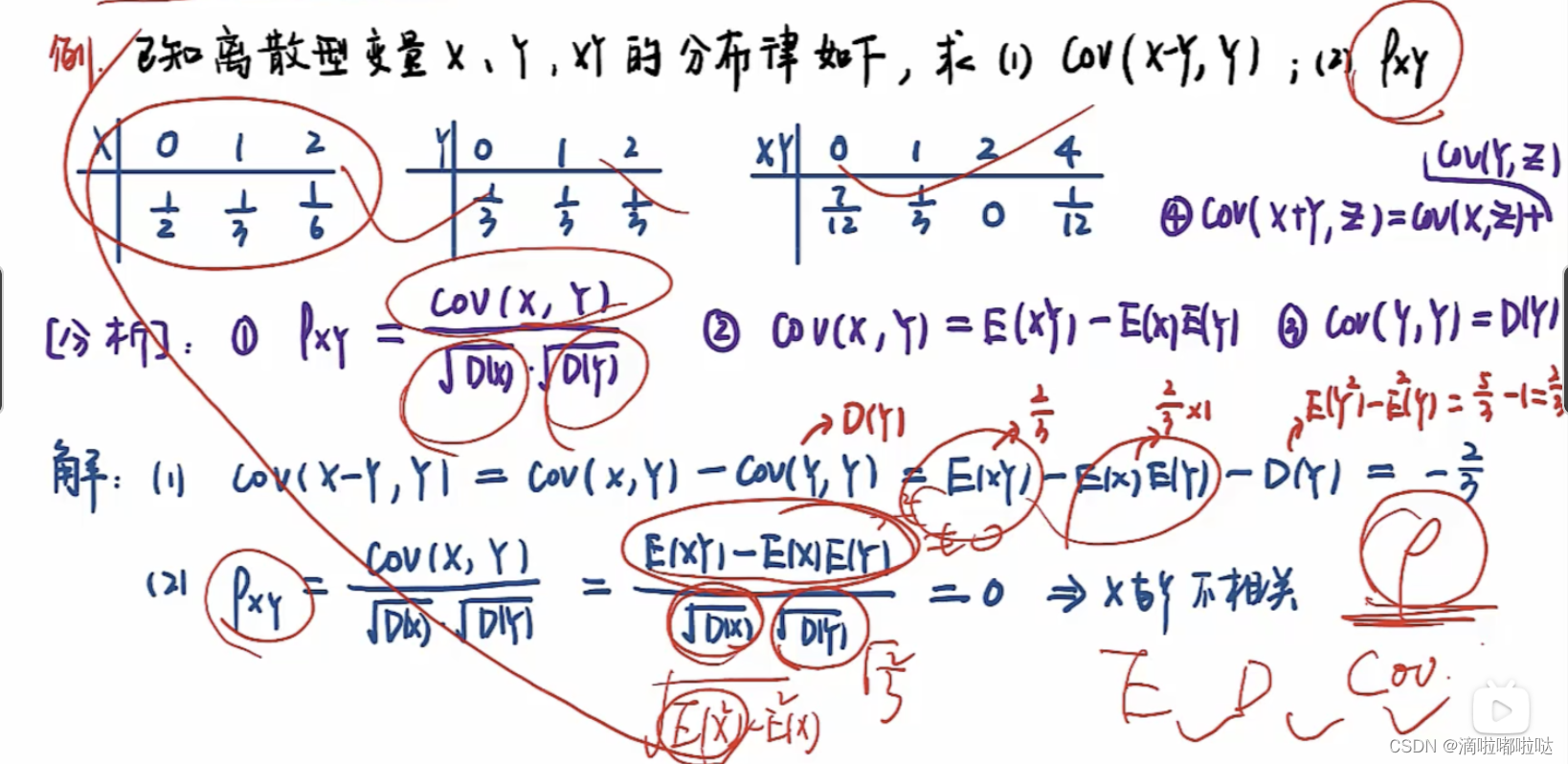
🌟注意由分布律算方差的方法：1.先算平方的期望，再减去期望的平方2.先算出期望，再用每个值减去期望再平方再乘对应的概率。

类似题：

考点3.连续型随机变量的协方差、相关系数

知识铺垫：

总结：

题目描述：

解题思路：

类似题：

第五、六章：大数定理、中心极限定理、数理统计基本概念

考点1.大数定律

知识铺垫：

可以看看：

大数定理的通俗理解（辛钦、伯努利、切比雪夫大数定理） - 知乎

总结：

题目描述：

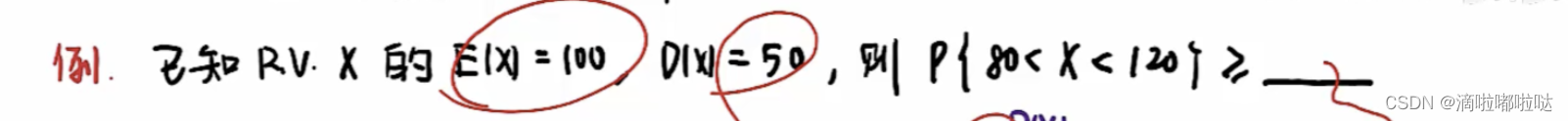
解题思路：

🌟直接套切比雪夫不等式

类似题：

考点2.中心极限定理

知识铺垫：

总结：

独立同分布的变量之和近似服从正态分布。

题目1描述：

解题思路：

🌟变量间相互独立，则它们和的期望等于期望的和，和的方差等于方差之和

类似题：

题目2描述：

解题思路：

🌟0-1分布的期望为p，方差为p（1-p）

类似题：

考点3.三个重要分布

知识铺垫：

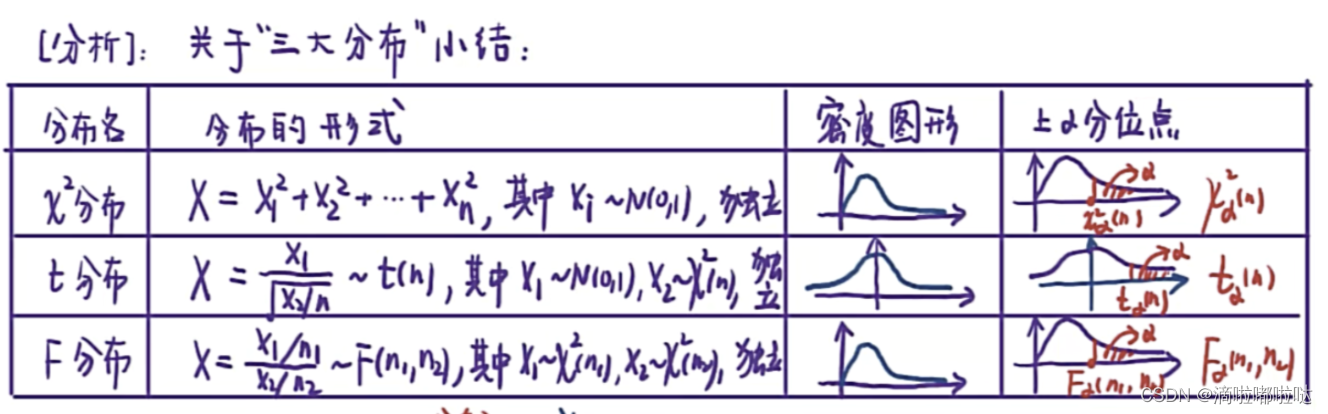
总结：

要记住三种分布对应的形式，以便在考试中灵活地使用。

1.卡方分布：正态分布平方之和

2.t分布：正态分布除以根下卡方除以n

3.F分布：“卡分之卡”

题目1描述：

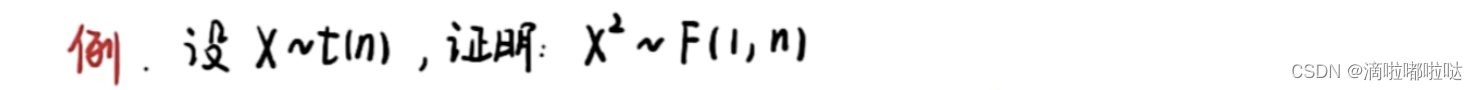
解题思路：

类似题：

题目2描述：

解题思路：

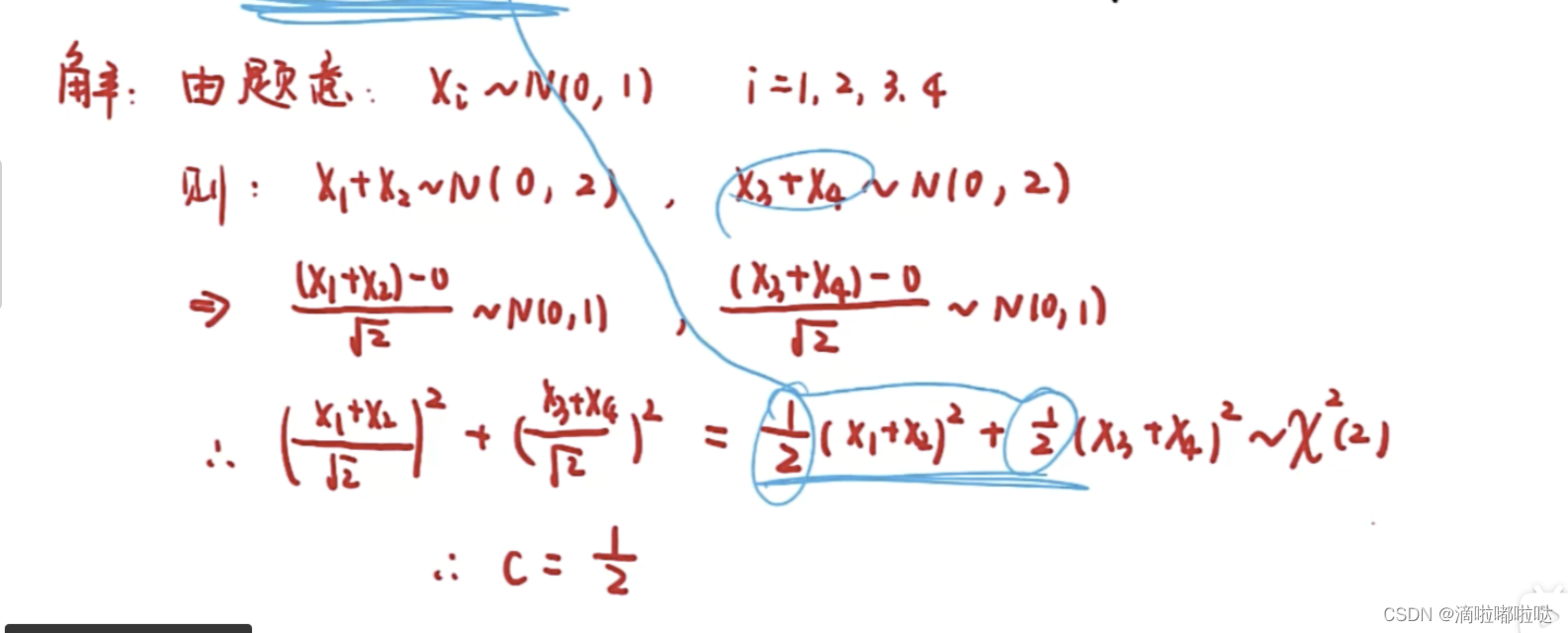
类似题：

第七章：参数估计

考点1.未知参数的矩估计和极大似然估计

知识铺垫：

总结：

先记住步骤流程（不难）。

关于矩估计：

什么是矩

矩估计的核心思想是用样本矩（其实就是均值）近似总体矩（即期望）（矩估计不唯一,为了计算简单，尽可能用低阶矩。）

关于极大似然估计：

核心思想是让样本发生的概率最大的参数值是最合理的，也就是说要让样本中各个数出现的概率之积最大。由此思想，便可理解极大似然估计每一步步骤的原因了：

构建样本似然函数（把概率之积表示出来，以便求其最大值）->取对数（取了对数才方便求导求驻点）->求导，求驻点（导数为零的点，原函数取极值）->求出的便是最合理的参数

题目描述：

解题思路：

🌟注意这里的似然函数的最后是 $(x_1x_2....x_n)^\theta$ 而不是 $x^{n\theta}$

类似题：

考点2.估计量的无偏性和有效性

知识铺垫：

总结：

无偏性：检验期望，看与总体对应的估计量是否有偏差

有效性：检验方差，看与总体对应估计量的差距

题目描述：

解题思路：

类似题：

最右边挡住的部分是 $e^{-\frac{\frac{t^2}{n\theta}}{-2}}$

考点3.未知参数的区间估计

知识铺垫：

可以看看这篇文章，里面讲述了枢轴变量是怎么求出来的（框框老师的建议是直接背下来）：【概率论】- (1)区间估计 - 知乎

总结：

什么叫计算置信区间：这一类题，都会让在一定的置信度下计算期望值或者是方差值的置信区间，其实就是让我们去算一个区间，期望值和方差值落在这个区间里的概率大于等于置信度。

为什么是算枢轴变量，再将枢轴变量放到区间中来算：在估计参数 $\mu$ 的置信区间是，用 $\overline{X}$ 来近似 $\mu$ ，但 $\overline{X}$ 服从的是一个一般的正态分布，所以要进行一些转化，如果总体方差已知，那就用标准化的流程将其转化为标准正态分布，如果总体方差未知，那就带入样本方差将其转化为t分布。

关于枢轴变量为啥在不同情况下是那样的形式，书上有这样四句定理

其中1，3的证明超过本书范围，而1，2，3结合可以发现可以推出来4

$\frac{\overline{X}-\mu}{S/\sqrt{n}} = \frac{\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}{\frac{S}{\sigma}} = \frac{\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}{\sqrt{\frac{S^2}{\sigma^2}}} = \frac{\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}{\sqrt{\frac{\frac{(n-1)·S^2}{\sigma^2}}{n-1}}} = \tau(n-1)$

这一部分的内容，靠背诵就能解决很多问题。

题目描述：

解题思路：

🌟这部分最高效率的方法是硬背，考试的时候查表就可以了。

我在学这部分时常常混淆一个概念：上侧分位数。

一定要记住，是点右侧部分的面积等于 $\alpha$

类似题：

第八章：假设检验

考点1.正态总体下均值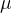 $\mu$ 的假设检验

知识铺垫：

总结：

其实假设检验与上面的区间估计很类似，区间估计是给一个置信度让求区间，而假设检验类似于它的逆过程，需要做的也是根据一个 $\alpha$ 求出拒绝域（查表即可），再将假设量带入假设检验量（实际就是枢轴变量），看它满不满足在拒绝域内，如果在就将其拒绝。

题目描述：

解题思路：

类似题：

考点2.正态总体下方差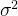 $\sigma ^2$ 的检验

知识铺垫：

总结：

题目描述：

解题思路：

类似题：

第九章

考点：线性回归

题目描述：

题目解答

总结

12.28初版，整体已完成。还有部分内容之后会持续更新。

12.28晚更，更新了大部分解释，剩余工作以补充习题为主。

评论 2

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。