归一化的三种常见方法

最新推荐文章于 2025-03-15 15:13:33 发布

Cheng-Kai

最新推荐文章于 2025-03-15 15:13:33 发布

阅读量2.6k

点赞数 25

分类专栏：机器学习文章标签：算法机器学习人工智能

本文链接：https://blog.csdn.net/m0_75210954/article/details/143242563

版权

机器学习专栏收录该内容

7 篇文章

订阅专栏

本文将介绍机器学习中经常能够遇见的三种归一化的方法，分别是最值法（最大最小值法），标准化法（包含均值归一化和方差归一化）。

为什么要进行归一化？

在进行梯度下降法的时候在不同的特征维度如果存在两个值差异比较大的情况，比如说年龄18岁收入100000rmb，我们都知道两者之间差距值特别大但是代表的物理含义不同，但是计算机如何知道？所以在进行梯度下降的时候就会产生问题。

假设输出 $y=\theta1 x1 + \theta 2x2$ ，一开始我们并不知道两部分哪个更重要，便认为两个等价，于是乎现在假设x1为18，x2为100000，则 $\theta 1$ >> $\theta 2$

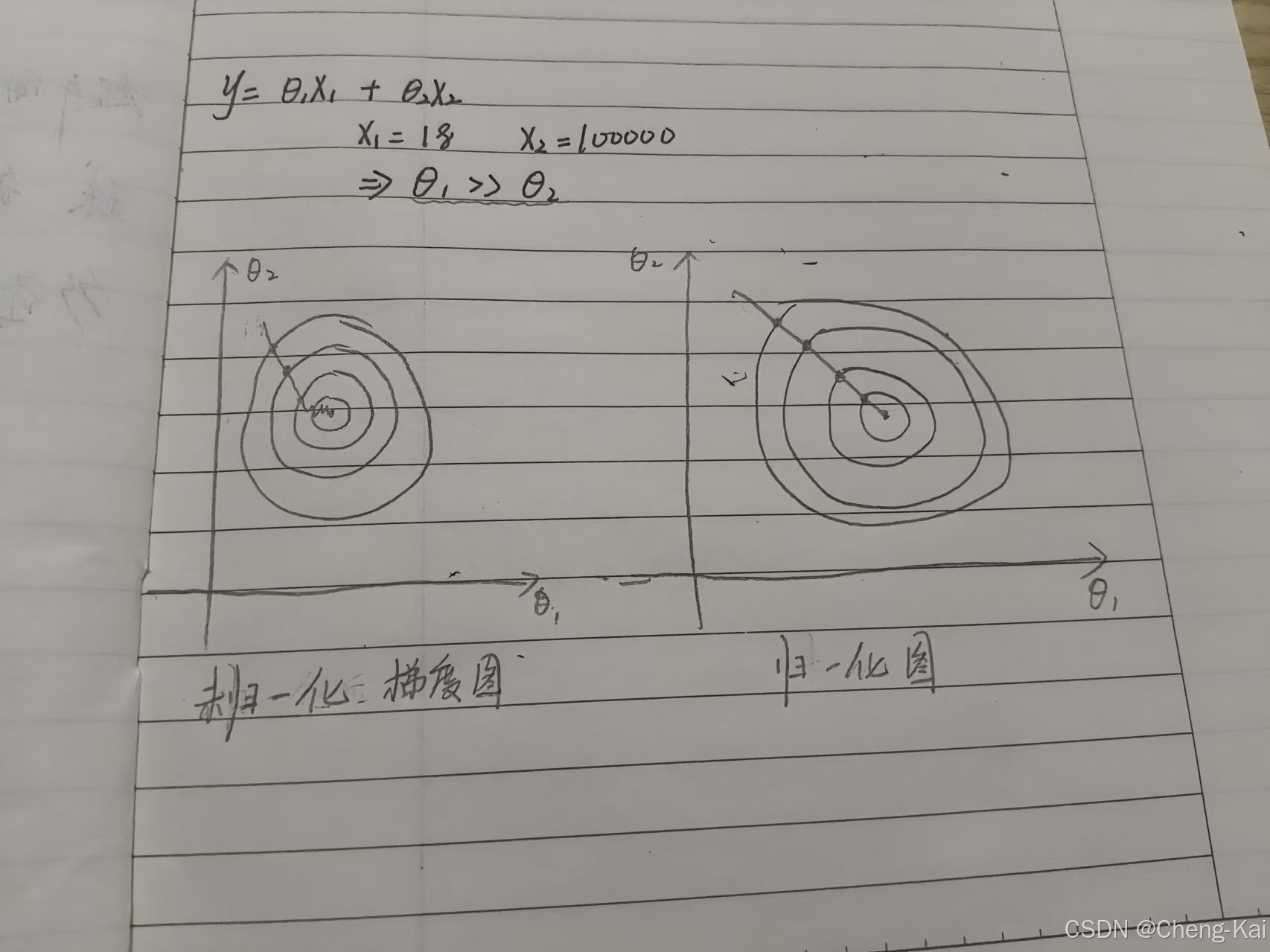
如图所示，左图未归一化的时候 $\theta 2$ 其实早就已经收敛，为了等 $\theta 1$ 而在来回震荡，右图归一化后 $\theta 1$ 和 $\theta 2$ 同时趋于收敛。

归一化的好处

1）归一化本来的作用就是为了让各个特征维度的theta调整幅度一致（当每个维度的theta都收敛才是最优解）。

2）归一化的附带好处是，消除了由于不同特征维度数量级相差很大造成的影响，减小预测结果的误差，提高模型的精度。例如KNN算法中，利用欧式距离计算未知点属于哪一个维度，欧式距离公式（二维）， $d = \sqrt{ ({x_{1}}-{x_{2}})^{2} +({y_1} - {y_2})^{2}}$ ,其实看这个公式容易被误导，其实在KNN算法中y并不是指的输出而是指的一个特征维度。可以看n维空间下的公式便于理解。由此可以知道，但凡其中一个维度的值数量级远远大于其他维度，则会导致d主要取决于这个数量级大的特征，可能会与实际情况相悖。

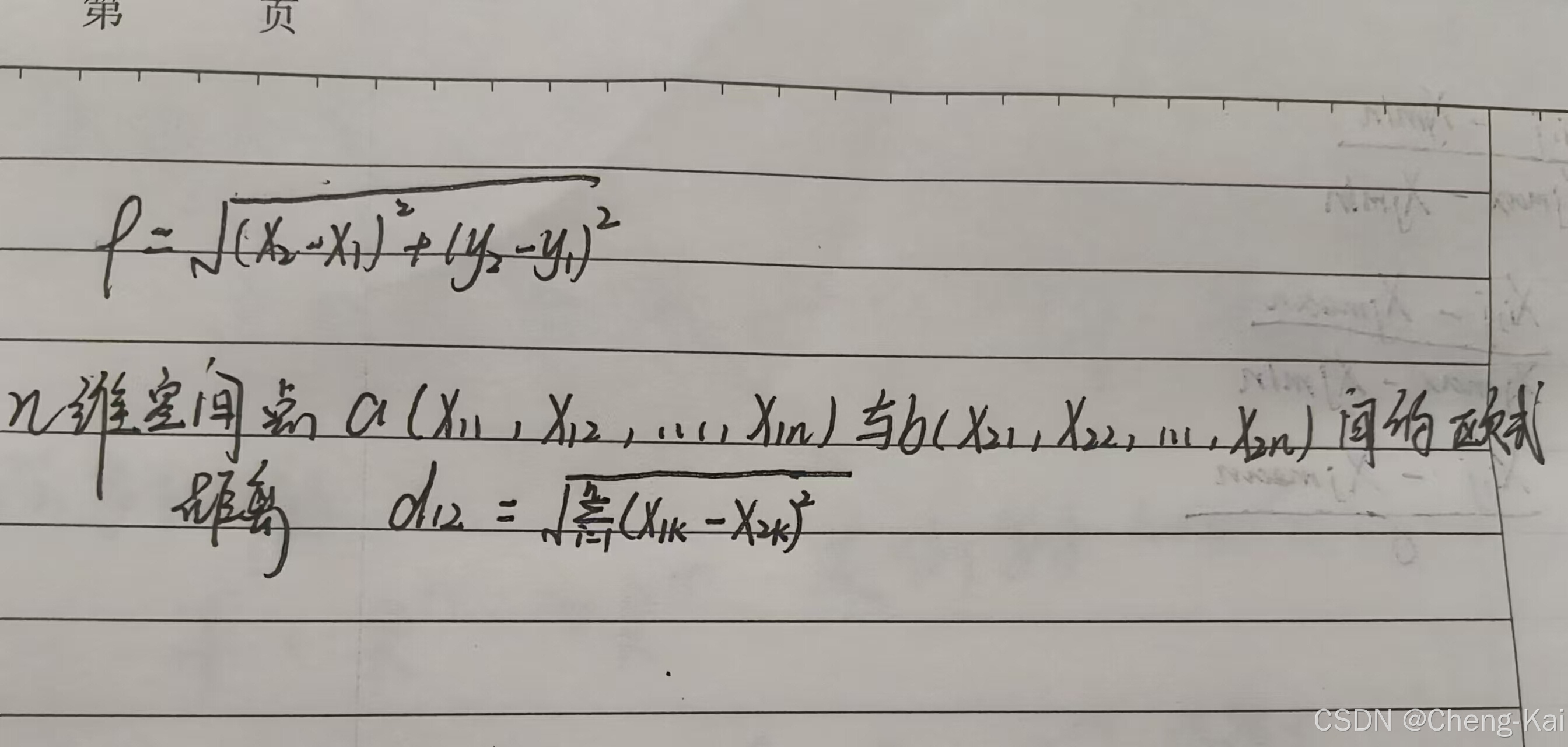
归一化的本质

归一化的本质就是进行无量纲化。

有一个很有趣的比喻，归一化好比是共同富裕，就是各个维度的theta同时趋于收敛，而没有归一化的梯度下降过程就好比是先富一部分，然后先富的等待后富，就是某个维度的theta先收敛完成在收敛区间震荡等待其他维度的theta去收敛。

归一化的方法

1）最大最小值法

数学表达

$X_{new_{i,j}} =\frac{ X_{i,j} - X_{jmin}}{X_{jmax}-X_{jmin}}$

$X_{new_{i,j}}$ 表示在i行j列归一化后的值， $X_{i,j}$ 表示第i行j列的值， $X_{jmin}$ 表示第j列最小值， $X_{jmax}$ 表示第j列最大值

代码实现

运行结果

优缺点

优点：将数据全部归于0-1的区间内。

缺点：受异常值影响很大，例如当最大值为100000，最小值为1的时候，分母相当大，有很大一部分数据约为0，一部分数据约为1，达不到我们想要的效果

2）均值法

数学表达

$X_{new_{i, j}} = \frac{X_{i,j}-X{jmean}}{X_{max}-X_{min}}$

$X_{jmean}$ 表示第j列的均值

代码实现

运行结果

优缺点

优点：在分子处使用了均值，减这个均值达到了一个什么好处，就是出现了负数。出现负数会让梯度下降的过程尽可能的走直线。

缺点：分母未变，也就是异常值的影响依然在。

3）方差法

数学表达

$X_{new_{i,j}} = \frac{X_{i,j}-X{jmean}}{\sigma }$

代码实现

运行结果

优缺点

优点：采用了标准差作为分母，对于异常点具有包容性，采用了均值作为分母，减少theta收敛的迭代次数。

缺点：不能将值归于0-1区间之内，其实在我看来这只是一个小瑕疵，并不影响方差法被使用的频率。

完整代码

from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
import numpy as np

scaler1 = MinMaxScaler()
X = np.array([[2,3,4],[3,5,6],[5,8,9]])
print(f"X矩阵：\n{X}")

scaler1.fit(X)
print(f"X最大最小归一化： \n{scaler1.transform(X)}")


scaler2 = StandardScaler()
scaler2.fit(X)
print(f"X标准化(方差归一化)： \n{scaler2.transform(X)}")

mean_1 = np.mean(X[:,0])
mean_2 = np.mean(X[:,1])
mean_3 = np.mean(X[:,2])
mean_ = np.array([[mean_1,mean_2,mean_3], [mean_1,mean_2,mean_3], [mean_1,mean_2,mean_3]])
max_1 = np.max(X[:,0])
max_2 = np.max(X[:,1])
max_3 = np.max(X[:,2])
min_1 = np.min(X[:,0])
min_2 = np.min(X[:,1])
min_3 = np.min(X[:,2])
max_ = np.array([[max_1,max_2,max_3], [max_1,max_2,max_3], [max_1,max_2,max_3]])
min_ = np.array([[min_1,min_2,min_3], [min_1,min_2,min_3], [min_1,min_2,min_3]])
# print(min_)
# print(max_)
# print(mean_)
# print(f"mean: {mean_} \nstd: {std_}")
mean_scaler = (X - mean_)/(max_ - min_)
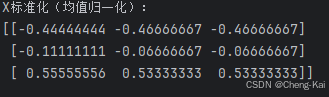
print(f"X标准化（均值归一化）：\n{mean_scaler}")

总结

在实际应用中最常使用的其实是第三种方法，前两种方法仅是用来学习的。在实际运用中使用归一法或者其他特征工程，有一个特别需要注意的地方，训练集和测试集数据都需要进行的归一化，而且在测试集中归一化使用的均值和方差应该是在训练集中算（fit）出来的，这么做的原因是让测试集和训练集符合同一分布（概率论知识）。