动态规划入门（求最长公共子序列）

最新推荐文章于 2024-04-24 22:43:13 发布
最新推荐文章于 2024-04-24 22:43:13 发布
阅读量793 收藏
点赞数
分类专栏： Dynamic Programming 文章标签： algorithm 动态规划 最长公共子序列 c++ methods
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m6830098/article/details/17513285
版权

        

        最长公共子序列是动态规划中的一道经典题目了，今天学习了一下。记录下其求解过程，并加深一下对动态规划的了解。


        题目：给定两个序列X 和 Y，称序列Z是X和Y的公共子序列，如果Z即使X的一个子序列，又是Y的一个子序列。在最长子序列问题中，给定两个序列X和Y，希望找出X和Y的最长公共子序列。这就是常见LCS问题。


        Example：

        X =  A B C B D A B        Y = B D C A B A    我们可以用肉眼看出来 X 和 Y 的最长公共子序列为 B C A B 和  B D A B， 答案不唯一。

 

        问题：对于 序列X [ 1，2.....m]， 序列 Y[ 1，2 .....n],找出序列X和Y的最长公共子序列。


        如何解决这个问题呢。我们首先会想到用一种蛮力的方法：

       方法1：

        我们首先枚举出来X的所有子序列，然后逐一检查 是否为Y的子序列，并且随时记录发现的最长子序列。我们称它为穷举法。

        对于这种解决问题的方法，我们先确定下它的时间复杂度大概是都少:


        1.首先求出X总共有多少个子序列，我们可以把  X[ 1， 2 .....m]序列，当做一个二进制的一个位串。每个位上可以选择1或者0，选择1表示该位被选中，选择0表示该位没有被选中，则 X的一个子序列就分别对应 一种情况，而 X 总共有m个位，每个位置上有2个选择，1 或者0，So 总共有 2^m个子序列。

        2.对应X的每个子序列，如何判断是否在Y中存在，这个很简单我们只需要在Y中扫描一遍就可以判断了，所以时间复杂度为o（n）

        所以这个穷举法对应的时间复杂度为 o（ n * 2^m ） 是 指数级时间复杂度，我们称这种方法的时间复杂度为 龟速。这显然 不是我们想要的方法。



      方法2：（Dynamic programming)


        我们需要简化和扩展上面的算法。先来定义几个符号：

        定义|S|为序列S 的长度，  定义 C[ i, j ]为 | LCS ( X[ 1,2 ...i], Y[ 1,2 ...j] )| （ 序列X[1,2...i] 和序列Y[1,2...j]的最长公共子序列的长度），  则 C[ m, n ] 就是序列X 和 Y的最长公共子序列长度。即C[ m, n] = | LCS （ X， Y ） |


        先来推倒出来一个公式，然后用剪切法加以证明：

 c[ i, j] =  c[ i - 1, j - 1] + 1                if x[ i ] == y[ j ];
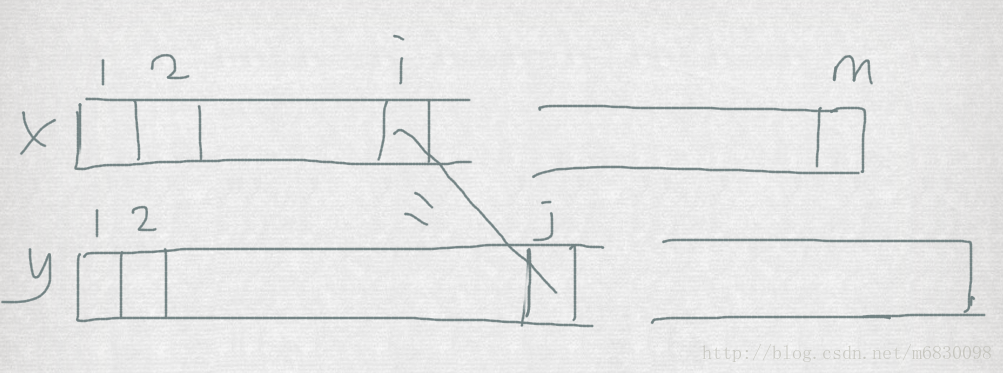
          =  max( c[ i - 1, j ] c[ i, j - 1 ])   other wise
        证明：

        case1： 在 x[ i ] == y[ j ] 的情况下， 假设 z[ 1,2 ....k ] 是 X 和 Y 的最长公共子序列， 那么我们可以推出 z[ k ] = x[ i ] = y[ j ], 且z[ 1,2....k - 1]是 Xm-1 和 Yn-1的一个 LCS ,且c[ i, j ] = k。如下图所示：


        反证法： 如果 序列z 不包含X[i]，所以我们可以添加X[i] 到z[ 1,2 ...k ]中（因为 x[ i ] = y[ j ] ,Match)，所以序列z中一定包含 x[i]，同理我们还可以推出 z[ 1,2 ... k -1 ] 是 LCS( x[ 1,2 ...i - 1], y[ 1,2.... j - 1])，这个也可以用反证法来证明，假设有个 序列w 是更长的公共子序列 （LCS( x[ 1,2 ...i - 1], y[ 1,2.... j - 1])） 则| w | > k - 1,然后我们同理可以在w 后面 加上x[ i ]，所以它可以变成一个更长的LCS ，其值大于 k，所以 得到与上文矛盾，则可以证明一个c[ i - 1, j - 1] = k - 1   ==> c[ i , j ] = c[ i - 1, j - 1] + 1;  

       case 1的 推论得到了证明，我们同理可以证明case 2的推论。


       case2： 如果z[ k ] 不等于 x[ i ] ，那么z是 x[ 1,2 ...i - 1] 和y[ 1,2 ...j]的一个 LCS，该问题用反证法就可以证明了。 如果 x[ 1,2 ...j - 1] 和y 有一个更长LCS W，则W 也肯定是x[ 1,2, ...i ] 和y[1,2...j]的一个LCS，与当前推论矛盾。如果z[ k ] 不等于y[ j ]，在z是x[1,2... i ] 和 y[ 1,2 ...j - 1]的一个LCS，同上可证明。


       动态规划的两个特征：

       1.最优子结构信息。 两个序列的一个LCS包含两个序列的前缀的一个LCS，所以说明本问题具有最优子结构信息。为了找出X 和Y的一个LCS，可能根据需要找出X 和Yn-1 的一个LCS以及Xm-1 和Y的一个LCS，这两个问题又同时包含Xm-1 和Yn-1的LCS 这个子问题，我们会从3个子问题中寻找一个最优的子问题解用到X和Y的一个LCS上。根据关系我们建立一个递归式：

          =  c[ i - 1, j - 1] + 1              if x[ i ] == y[ j ] && i > 0 && y > 0
c[ i, j]  =  max( c[ i - 1, j ] c[ i, j - 1 ]) if x[ i ] != y[ j ] && i > 0 && j > 0
          =  0                                 if x = 0 || y == 0
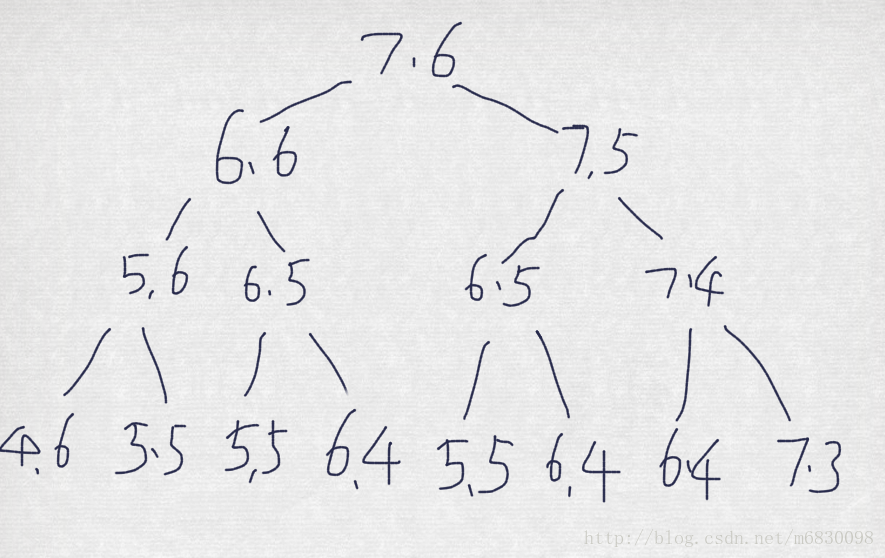
          寻找问题最优解的时候 需要在3个子问题中做选择，其余2个会被排除掉。


      我们可以根据这个表达式轻易的写出一个指数时间的递归算法，我们可以看出来 当x[ i] != y[ j ]的情况下比较糟糕，我们会需要计算两个子问题的解。 下面用一张图来模拟下递归算法的运行，只模拟x[i] != y[j]的情况，看递归树是如何运行的。假设m = 7， n = 6.


        树的高度是m+n（看最右边的分支即可看出来） ,所以我们直接递归的话时间复杂度会是2^（m+ n），还是龟速。

        但是我们可以在树中看到，做了很多重复的计算和工作，比如第三排的 6，5 第四排的6，4  ，如果采用递归的方法的话，这些都是要重复计算的。我们有个经验就是不要做重复的计算。下面就是动态规划的第二个特点了



       动态规划的第二个特点：重叠子问题

       一个递归的方法会包含了很少数量的独立子问题，其余的都是在重复的计算。而对于Xm和Yn 这两个序列来说，其子问题的空间为o（mn）。

       我们可以采取做备忘录的方法来解决这个重复计算的问题。

       伪代码：

    定义c[m][n]，并且初始化，然后在求c[i][j]的时候
    if c[ i ][ j ] == nil
        then compute it 根据我们上面的那个公式
    else
        return c[ i ][ j ];

          可以得出这个的时间复杂度为o(mn)，空间复杂度也为o（mn）.根据动态规划来自底向上计算。



       例题：点击打开链接 POJ 1458

       代码：

//
//  main.cpp
//  LCS
//
//  Created by mini on 12/23/13.
//  Copyright (c) 2013 mini. All rights reserved.
//


#include <iostream>
#include <string>
using namespace std;

#define SIZE 999

int dp[ SIZE ][ SIZE ] = { 0 };
int Max( int & x, int & y ){
    return x > y ? x : y;
}
int main(int argc, const char * argv[])
{
    int i, j;
    string str1,str2;;
    size_t len1, len2;
    while( cin >> str1 >> str2 ){
        memset( dp, 0, sizeof( dp ) );
        len1 = str1.length();
        len2 = str2.length();
        for ( i = 1; i <= len1; i++ ) {
            for ( j = 1; j <= len2; j++ ) {
                if( str1[ i - 1 ] == str2[ j - 1 ] )
                    dp[ i ][ j ] = dp[ i - 1][ j - 1] + 1;
                else {
                    dp[ i ][ j ] = Max( dp[ i - 1 ][ j ], dp[ i ][ j - 1 ] );
                }
            }
        }
        cout << dp[ len1 ][ len2 ] << endl;
    }
    return 0;
    
}


        如果想得到LCS的路径，可以另外使用一个数组，记录走的路线。

//
//  main.cpp
//  LCS
//
//  Created by mini on 12/23/13.
//  Copyright (c) 2013 mini. All rights reserved.
//


#include <iostream>
#include <string>
#include <stack>
using namespace std;

#define SIZE 999

int dp[ SIZE ][ SIZE ] = { 0 };
char position[ SIZE ][ SIZE ];
int Max( int & x, int & y ){
    return x > y ? x : y;
}
void PrintLCS( char p[ ][ SIZE ], string str, int i, int j ){
    if( i < 1 || j < 1 )
        return ;
    if ( p[ i ][ j ] == '=' ) {
        PrintLCS( p, str, i - 1, j - 1 );
        cout << str[ i - 1 ] << " ";
    }
    else if( p[ i ][ j ] == '^' )
        PrintLCS( p, str, i - 1, j );
    else
        PrintLCS( p, str, i , j - 1 );

}
int main(int argc, const char * argv[])
{
    size_t i, j;
    string str1,str2;;
    size_t len1, len2;
    while( cin >> str1 >> str2 ){
        memset( dp, 0, sizeof( dp ) );
        len1 = str1.length();
        len2 = str2.length();
        for ( i = 1; i <= len1; i++ ) {
            for ( j = 1; j <= len2; j++ ) {
                if( str1[ i - 1 ] == str2[ j - 1 ] ){
                    dp[ i ][ j ] = dp[ i - 1][ j - 1] + 1;
                    position[ i ][ j ] = '=';//找到相等元素
                }
                else {
                    if ( dp[ i - 1 ][ j ] >= dp[ i ][ j - 1 ] ) {
                        dp[ i ][ j ] = dp[ i - 1 ][ j ];
                        position[ i ][ j ] = '^';
                    }
                    else{
                        dp[ i ][ j ] = dp[ i ][ j - 1 ] ;
                        position[ i ][ j ] = '<';
                    }
                    
                }
            }
        }
        cout << dp[ len1 ][ len2 ] << endl;
        i = len1;
        j = len2;
        stack< char > s;
        while( 1 ){
            if( i < 1 || j < 1 )
                break;
            if ( position[ i ][ j ] == '=' ) {
                s.push( str1[ i - 1 ] );
                i--;
                j--;
            }
            else if( position[ i ][ j ] == '^' ){
                i--;
            }
            else if( position[ i ][ j ] == '<' ){
                j--;
            }
        }
        char p;
        while( !s.empty() ){
            p = s.top();
            s.pop();
            cout << p << " ";
        }
        cout << endl;
        PrintLCS( position, str1, (int)len1, (int)len2 );
        cout << endl;
    }
    return 0;
    
}




        改进代码：一旦设计出某算法后，常常可以在时间或者空间上对算法进行改进。

        1.我们可以完全去掉记录路径信息的数组，因为每个表dp[i][j]的值取决于Max（dp[i - 1][j],dp[i][j-1])，或者dp[i-1][j-1]，所以我么可以根据给定c[i][j]的值，进行判断，在o（1）时间内判断c[i][j]是根据这3个之中的哪个判断出来的。所以根本不需要额外的数组来专门记录路径。

        Code:

#include <iostream>
#include <string>
using namespace std;

#define SIZE 999

int dp[ SIZE ][ SIZE ] = { 0 };
int Max( int & x, int & y ){
    return x > y ? x : y;
}
void PrintLCS( int dp[ ][ SIZE ], string str1, string str2, int i, int j ){
    if( i < 1 || j < 1 )
        return ;
    if ( str1[ i - 1 ] == str2[ j - 1 ] && dp[ i ][ j ] == (dp[ i - 1 ][ j - 1 ] + 1 ) ) {
        PrintLCS( dp, str1, str2, i - 1, j - 1 );
        cout << str1[ i - 1 ] << " ";
    }
    else if( dp[ i ][ j ] == dp[ i - 1 ][ j  ] )
        PrintLCS( dp, str1, str2, i - 1, j );
    else
        PrintLCS( dp, str1, str2, i , j - 1 );
    
}
int main(int argc, const char * argv[])
{
    int i, j;
    string str1,str2;;
    size_t len1, len2;
    while( cin >> str1 >> str2 ){
        memset( dp, 0, sizeof( dp ) );
        len1 = str1.length();
        len2 = str2.length();
        for ( i = 1; i <= len1; i++ ) {
            for ( j = 1; j <= len2; j++ ) {
                if( str1[ i - 1 ] == str2[ j - 1 ] )
                    dp[ i ][ j ] = dp[ i - 1][ j - 1] + 1;
                else {
                    dp[ i ][ j ] = Max( dp[ i - 1 ][ j ], dp[ i ][ j - 1 ] );
                }
            }
        }
        cout << dp[ len1 ][ len2 ] << endl;
        PrintLCS( dp, str1, str2, (int)len1, (int)len2 );
        cout << endl;
    }
    return 0;
    
}

            这里需要注意的一点是。不能直接根据dp[i][j] = dp[ i - 1] [j - 1] + 1,就判断有相同的元素，还需要实际上去判断字符串上i，j位置上元素是否相同。


        我们可以继续优化代码，在求dp[i][j]的时候，只会用到dp的两行，即被计算的那一行和前面一行，所以我们可以用2行的数组就可以搞定，空间复杂度继续降低o（2n）

        Code:

Source Code

Problem: 1458		User: m68300981
Memory: 248K		Time: 16MS
Language: C++		Result: Accepted
Source Code
#include <iostream>
#include <string>
using namespace std;

#define SIZE 999

int dp[ 2 ][ SIZE ];//仅仅用2行来求最大值
int Max( int & x, int & y ){
    return x > y ? x : y;
}
int main(int argc, const char * argv[])
{
    int i, j;
    string str1,str2;;
    size_t len1, len2;
    while( cin >> str1 >> str2 ){
        memset( dp, 0, sizeof( dp ) );
        len1 = str1.length();
        len2 = str2.length();
        for ( i = 1; i <= len1; i++ ) {
            for ( j = 1; j <= len2; j++ ) {
                if( str1[ i - 1 ] == str2[ j - 1 ] )
                    dp[ 1 ][ j ] = dp[ 0 ][ j - 1] + 1;
                else {
                    dp[ 1 ][ j ] = Max( dp[ 0 ][ j ], dp[ 1 ][ j - 1 ] );
                }
            }
            for ( int k = 1; k <= len2; k++ ) {
                dp[ 0 ][ k ] = dp[ 1 ][ k ];
            }
        }
        cout << dp[ 1 ][ len2 ] << endl;
    }
    return 0;
    
}


        继续优化代码，可以使用dp的一行来更新，另外使用两个变量一直记录dp[i-1][j-1]和dp[i-1][j]的值，dp的一行也让然可以继续优化，使用两个字符串中的那个值比较小的那个。

        Code：

Source Code

Problem: 1458		User: m68300981
Memory: 240K		Time: 16MS
Language: C++		Result: Accepted
Source Code
#include <iostream>
#include <string>
using namespace std;

#define SIZE 999

int main(int argc, const char * argv[])
{
    int i, j;
    string str1,str2;;
    size_t length1, length2;     //两个字符串的长度
    int leftTop, top;     //记录当前c[i][j]的上边的值和左上的值
    while( cin >> str1 >> str2 ){
        if ( str1.length() > str2.length() ) {    //始终让str1的长度小于str2的长度
            string temp;
            temp = str1;
            str1 = str2;
            str2 = temp;
        }
        length1 = str1.length();
        length2 = str2.length();
        int * dp = new int[ length1 ];
        memset( dp, 0, sizeof(int) * length1 );
        int temp;
        leftTop = dp[0];
        top = dp[1];
        for ( i = 1; i <= length2; i++ ) {
            for ( j = 1; j <= length1; j++ ) {
                temp = dp[j];
                if ( str1[ j - 1] == str2[ i - 1 ] ) {
                    dp[ j ] = leftTop + 1;
                }
                else{
                    dp[ j ] = top > dp[ j - 1 ] ? top : dp[ j - 1 ];
                }
                if ( j == length1 ) {
                    top = dp[ 1 ];
                    leftTop = dp[0];
                }
                else{
                    leftTop = temp;
                    top = dp[ j + 1 ];
                }
            }
        }
        cout << dp[ length1 ] << endl;
        
    }
    return 0;
    
}



       




        

        

慢慢来比较快
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
动态规划入门动态规划入门
01-06
动态规划入门动态规划入门动态规划入门动态规划入门动态规划入门
【动态规划入门】最长公共子序列
D_D_zy的博客
03-07 222
动态规划系列之一：子系列问题。 最长公共子序列问题和最长重复子数组类似，但是一个要求连续，一个要去不连续。连续不连续是非常重要的一个因素，因此要特别注意。
算法复习——动态规划篇之最长公共子序列问题
NickHan_cs的博客
01-25 1068
算法复习——动态规划篇之最长公共子序列问题 以下内容主要参考中国大学MOOC《算法设计与分析》，墙裂推荐希望入门算法的童鞋学习！ 1. 问题背景 子序列：将给定序列中零个或多个元素（如字符）去掉后所得结果 公共子序列： 给定两个序列XXX和YYY 公共子序列示例 ​ 问题是如何求两个给定序列的最长公共子序列？ 2. 问题定义 最长公共子序列问题（Longest Common Subsequence Problem） 输入： 序列X=<x1,x2,…,xn>X=<x_
动态规划入门---最长公共子序列
m0_45880587的博客
02-15 892
动态规划动态规划（DP,Dynamic Programming）定义动态规划问题的特点最长公共子序列问题（LCS）。分析实现特点动态规划的精髓总结作业 动态规划（DP,Dynamic Programming） ​ 我认为动态规划是所有算法中最最重要的，也是最最难的。在我看来它也是真正意义上省时间一种算法，除此之外的其它算法我姑且称之为暴力算法。它主要是用空间来换取时间，这是很值的，因为它将指数级别的时间复杂度直接降为多项式级别。这个寒假搞懂太值了。 定义 ​ 动态规划的核心思想就是把原问题分解
动态规划入门之最长公共子序列（LCS）
kerryfish的专栏
05-12 2045
LCS是动态规划在字符串问题中应用的典型。问题描述：给定一个序列，
动态规划入门（五）最长公共子序列（LCS）
z2656453168的博客
10-14 105
动态规划入门（五）最长公共子序列（LCS） 1143. 最长公共子序列 LCS是一类经典的二维dpdpdp问题，设字符串长度分别为mmm，nnn 0≤i<m0≤i<m0≤i<m，0≤j<n0≤j<n0≤j<n 则我们可以用dp[i][j]dp[i][j]dp[i][j]表示text1text1text1的前iii个序列和text2text2text2的前jjj个序列的最长公共子序列，则dp[i][j]dp[i][j]dp[i][j]的转移方程为 dp[i][j]=dp[i
动态规划入门动态规划入门动态规划入门动态规划入门
01-06
动态规划入门
动态规划入门第4、5课
08-06
动态规划入门第4、5课
动态规划入门第3课的PPT
08-06
动态规划入门第3课的PPT
动态规划入门
12-18
从深搜发现问题，从搜索树看重叠子问题和最优子结构，理解动态规划的思想。
C++教学——从入门到精通 10.循环
QIPABOSHI的博客
04-24 366
一些事嘛，需要重复做，这就是循环在开始学之前我提一个事，最好先学Python再学C++，不然就会像我和piaojunhe_0825一样有C++后遗症，在Python里写了一个for(int i=0;i
C++ WebServer的细节理解
我的博客
04-22 621
在非阻塞模式下，如果 I/O 操作不能立即完成（例如，因为没有数据可读 或 写缓冲区满），系统不会让调用进程阻塞等待，而是立即返回一个错误（通常为 EAGAIN 或 EWOULDBLOCK）。先查询文件描述符 fd 当前的标志，然后将 O_NONBLOCK 标志加入其中，并通过 F_SETFL 来更新文件描述符，最终实现将该文件描述符切换为非阻塞模式。这意味着，如果没有待处理的连接请求（即没有客户端尝试连接到服务器），accept() 会一直阻塞，直到有新的连接请求到达或发生其他特定条件（如超时）为止。
笨蛋学C++【C++基础第六弹】
YSL_Monet的博客
04-24 817
定义类需要用到关键字 class，然后指定类的名称，类的主体是包含在一对花括号中，主体包含类的成员变量和成员函数class 类名{访问修饰符（public/protected/private）:成员变量;成员函数();
【C++风云录】精益求精：探索C++开发中的性能优化艺术
记录我的学习历程
04-21 1102
本文将介绍几个在C++开发中常用的性能分析工具和性能优化工具集，包括PerfTools、gperftools、Valgrind、Intel VTune、PAPI以及Boost.Profile。通过深入了解这些工具的功能和用途，读者可以更好地理解如何利用它们来提高代码的执行效率和资源利用率。
C++——初识模板
qq_74245477的博客
04-22 911
之前实现的数据结构，比如栈，我们为了便于修改存储的数据类型，通常使用typedef来重定义数据类型，但是这样有一个缺陷，会导致我们定义的栈存储的都是一种数据，如果同时需要两个栈，一个存储int，一个存储自定义类型，那么typedef就不管用了。比如：当用int类型使用函数模板时，编译器通过对实参类型的推演，将T确定为int类型，然后产生一份专门处理int类型的代码，对于字符类型也是如此。概念：函数模板代表了一个函数家族，该函数模板与类型无关，在使用时被参数化，根据实参类型产生函数的特定类型的版本。
理解C语言中的位操作和整数类型：一个温度传感器读取问题的解析
最新发布
qq_61637982的博客
04-24 234
当我们编写嵌入式系统的代码时，我们经常需要使用位操作来处理硬件设备的数据。然而，如果我们对C语言的位操作和整数类型不完全理解，可能会遇到一些难以理解的问题。在这篇博客中，我将通过一个实际的例子来解释这些概念，并提供一个解决方案。
C++中的抽象类
hh121386的博客
04-23 200
C++中的抽象类
LeetCode //C - 18. 4Sum
Made in Code
04-22 794
【代码】LeetCode //C - 18. 4Sum。
CSAPP | Lab2-Bomb Lab详细解析
wangs29的博客
04-24 1254
邪恶的邪恶博士在我们班的机器上安放了大量的“二元炸弹”。二进制炸弹是一个由一系列阶段组成的程序。每个阶段都要求你在 stdin 上键入一个特定的字符串。如果你键入了正确的字符串，那么这个阶段就会被拆除，炸弹就会进入下一个阶段。否则，炸弹会通过打印“ BOOM 然后终止。当每个阶段都被拆除时，炸弹就会被拆除。我们要处理的炸弹太多了，所以我们给每个学生一个炸弹去拆除。你们的任务，你们别无选择，只能接受，就是在due date前拆除炸弹。祝你好运，欢迎加入拆弹小组！
动态规划入门csdn
09-13
动态规划在解决一些经典问题中有着广泛的应用，比如最长递增子序列、0-1背包问题等。动态规划的理论和方法在计算机科学领域具有重要的意义，并且可以应用于其他领域，如经济学、生物学等。 总之，动态规划是一种...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值