背包问题
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。
Example:
在下面的图中,应该选择哪些盒子,才能使得价格尽可能的大,而保持重量小于或等于15KG?

0/1背包问题:
 图片来源:维基百科
图片来源:维基百科
像这种求最优解的题目一般都可以用动态规划来解决的,如果我们要用动态规划来做,我们需要找到的状态和状态转移方程。 我们以上图中的问题为例,现在有5个元素可供我们选择,对当前的任何一个元素我们有两种方式,放入背包(不放入背包),0/1背包的关键点就是如何有效的利用背包的剩余重量,找出最好的物品组合方式。使得其中物品价值最大。
下面可以一步一步分析,当前有5个元素,我们对其中的每个元素都做两种选择,放入或者不放入背包。
1首先我们把价值为10的那个放入背包,书包价值+10 = 10,重量-4 = 11,余下的子问题是如何在剩下的4个元素中组合元素使得重量为11的包价值最大。
2.我们可以不把价值为10的那个元素放入背包,书包价值=0,重量=15,余下的子问题就是如何在剩下的4个元素中组个元素使得重量为15的包价值最大。
写到这里应该可以看出来,这符合动态规划的特征:最优子结构,下一步我们需要形式化的来表达出来原问题与子问题的关系
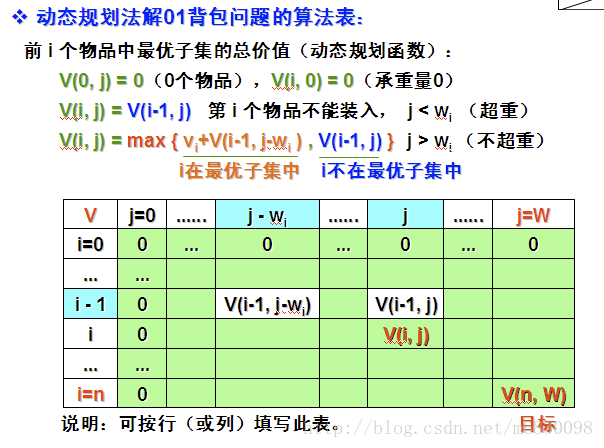
定义 dp( n, w )代表从n个元素中选择组合方式使得重量为w的背包价值最大,value( n )表示第n个元素的价值,weight( n )表示第n个元素的重量。则可以得到状态转移方程:
dp(n,w) = max( dp(n-1,w), dp(n-1,w-weight(n))+value(n))
// dp(n-1,w)表示物品不放入背包,从剩下n-1个元素中,书包重量为w中获取最大价值
// dp(n-1,w-weight(n))+value(n)表示第n个元素放入书包中(w > w - weight(n)然后我们去构造dp数组,构造完成之后dp( n, w ) 即为我么想要的答案。0/1背包可以有很多问题,例如求背包可获取的最大价值,背包中有哪些物品,背包的物品有哪些不同的组合方式.下面用代码的方式一一解决这些问题。
计算背包可获取的最大的价值.
 图片来源:百度图片.
图片来源:百度图片.
Code:bottom-up (自底向上计算解)
const int N = 100; //物品个数
const int M = 10000; //背包重量
int value[ N ],weight[ N ]; //物品价值和重量
int dp[ N + 1 ][ M + 1 ]; //dp数组
//构造dp数组
void knapsack( int n, int w ){//n表示个数,w表示重量
memset( dp, 0, sizeof( dp ) );
int i, j;
for ( i = 1; i <= n; i++ ) { //穷举每个物品,物品编号从1开始
for ( j = 0; j <= w; j++ ) { //穷举每个重量
if( j - weight[ i ] < 0 )
//重量达不到只能不放入
dp[ i ][ j ] = dp[ i - 1 ][ j ];
else
dp[ i ][ j ] = max( dp[ i - 1 ][ j ], dp[ i - 1 ][ j - weight[ i ] ] + value[ i ] );
}
}
cout << dp[ n ][ w ] << endl;
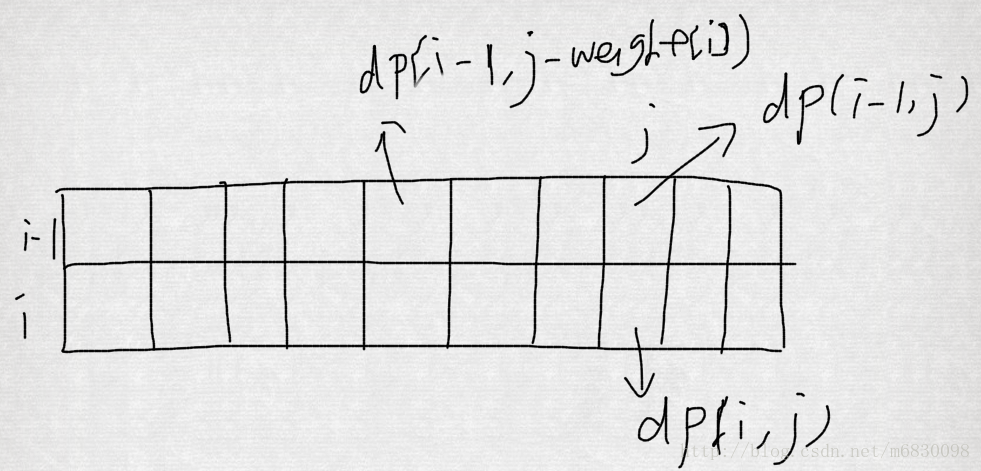
}动态规划的初始解法一般都可以优化,对dp数组进行优化,我们根据上面的算法可以得出来dp[i][j]只与它上方的值和左上方的另外一个值相关,我们可以只建立一个一维数组,根据它的记忆性,来不断更新这个一维数组就可以了.
因为dp[i][j]的值会用到其左上的dp[i-1][j-weight[i]]的值,所以我们选择从后边来进行更新。从后往前更新,这样就不会影响到前面的值。
Code:bottom-up(dp 数组用一维数组来更新)
const int N = 100; //物品个数
const int M = 10000; //背包重量
int value[ N ],weight[ N ]; //物品价值和重量
int dp[ M + 1 ]; //dp数组
//构造dp数组
void knapsack( int n, int w ){//n表示个数,w表示重量
memset( dp, 0, sizeof( dp ) );
int i, j;
for ( i = 1; i <= n; i++ ) { //穷举每个物品
for ( j = w; j - weight[ i ] >= 0; j-- ) { //穷举每个重量
dp[ j ] = max( dp[ j ], dp[ j - weight[ i ] ] + value[ i ] );
}
}
cout << dp[ w ] << endl;
}
时间复杂度为o(nw),空间复杂度为o(M),n是物品个数,M为背包的重量限制。
一般在面试的时候或者ACM题目中,肯定是会选择一维数组这种,二维的空间复杂度太高了,在ACM题目中一般会超出给定内存限制的。
另外一种解法:Code:top-down(从上往下,这个使用的使Memo-ization Algorithm 备忘录法)
#define INF -10000;
const int N = 100; //物品个数
const int M = 10000; //背包重量
int value[ N ],weight[ N ]; //物品价值和重量
int dp[ N + 1 ][ M + 1 ]; //dp数组
//构造dp数组
int knapsack( int n, int w ){//n表示个数,w表示重量
if( w < 0 ) return INF;
if( n == 0 ) return 0;//没有物品的时候返回0
//Memo-ization,如果值存在直接返回
if( dp[ n ][ w ] ) return dp[ n ][ w ];
return dp[ n ][ w ] = max( knapsack( n - 1, w ),
knapsack( n - 1, w - weight[ n ] ) + value[ n ] );
}POJ练习题目:点击这里(用一维数组,否则会内存超出限制的).
如何求出背包中放入哪些物品.
const int N = 100; //物品个数
const int M = 200; //背包重量
int value[ N ],weight[ N ]; //物品价值和重量
int dp[ M + 1 ]; //dp数组
int path[ N + 1 ][ M + 1 ];//记录元素是放还是不放,1表示存放,0表示不存放,初始化为0
//构造dp数组
void knapsack( int n, int w ){//n表示个数,w表示重量
memset( dp, 0, sizeof( dp ) );
memset( path, 0, sizeof( path ) );
int i, j;
for ( i = 1; i <= n; i++ ) { //穷举每个物品
for ( j = w; j - weight[ i ] >= 0; j-- ) { //穷举每个重量
//如果满足下面条件则更新,如果不满足则保持不变
if ( dp[ j - weight[ i ] ] + value[ i ] > dp[ j ] ) {
dp[ j ] = dp[ j - weight[ i ] ] + value[ i ];
path[ i ][ j ] = 1; //表示放入背包
}
}
}
cout << dp[ w ] << endl;
for ( i = n, j = w; i >= 1; i-- ) {
if ( path[ i ][ j ] ) {
cout << " 背包里元素 " << i << endl;
j -= weight[ i ];
}
}
}const int N = 100; //物品个数
const int M = 200; //背包重量
int value[ N ],weight[ N ]; //物品价值和重量
int dp[ N + 1 ][ M + 1 ]; //dp数组
//构造dp数组
void knapsack( int n, int w ){//n表示个数,w表示重量
memset( dp, 0, sizeof( dp ) );
int i, j;
for ( i = 1; i <= n; i++ ) { //穷举每个物品,物品编号从1开始
for ( j = 0; j <= w; j++ ) { //穷举每个重量
if( j - weight[ i ] < 0 )
//重量达不到只能不放入
dp[ i ][ j ] = dp[ i - 1 ][ j ];
else
dp[ i ][ j ] = max( dp[ i - 1 ][ j ], dp[ i - 1 ][ j - weight[ i ] ] + value[ i ] );
}
}
cout << dp[ n ][ w ] << endl;
//反过来推是否
for ( i = n ,j = w; i >= 1; i-- ) {
if ( j - weight[ i ] >= 0 && dp[ i ][ j ] == dp[ i - 1 ][ j - weight[ i ] ] + value[ i ] ) {
cout << "元素" << i << "放入到背包内" << endl;
j = j - weight[ i ];
}
}
}如何求背包最大价值的时候里面的物品有哪些不同的组合方式:
const int N = 100; //物品个数
const int M = 200; //背包重量
int value[ N ],weight[ N ]; //物品价值和重量
int dp[ M + 1 ]; //dp数组
int record[ N + 1 ][ M + 1 ];
int path[ N ];
void find_path( int n, int w, int num ){//n代表第n个元素,w代表背包剩余价值,num代表组合中有几个元素了,用于打印输出判断值的
static int pathNumber = 1;
if ( n < 1 ) {
cout << "This is the " << pathNumber++ << " Path :" << endl;
for ( int i = 1; i < num; i++ ) {
cout << path[ i ] << " ";
}
cout << endl;
return;
}
if ( record[ n ][ w ] == 0 ){ //不放入背包
find_path( n - 1, w, num );
}
else if ( record[ n ][ w ] == 1 ){
path[ num ] = n;
find_path( n - 1, w - weight[ n ], num + 1 );
}
else if ( record[ n ][ w ] == 2 ){//可以选择放或者不放,两种选择
path[ num ] = n;
find_path( n - 1, w - weight[ n ], num + 1 );
//不放入背包之后调用这个
find_path( n - 1, w, num );
}
}
//构造dp数组
void knapsack( int n, int w ){//n表示个数,w表示重量
memset( dp, 0, sizeof( dp ) );
memset( record, 0, sizeof( record ) );
int i, j;
for ( i = 1; i <= n; i++ ) { //穷举每个物品,物品编号从1开始
for ( j = w; j - weight[ i ] >= 0; j-- ) { //穷举每个重量
if ( dp[ j - weight[ i ] ] + value[ i ] < dp[ j ]) {
record[ i ][ j ] = 0;// 第i个元素不放入背包
}
else if ( dp[ j - weight[ i ] ] + value[ i ] > dp[ j ] ){
record[ i ][ j ] = 1; //第i个元素应该放入背包
dp[ j ] = dp[ j - weight[ i ] ] + value[ i ];
}
else{//相等的情况下,可以选择放入也可以选择不放入背包
record[ i ][ j ] = 2;
}
}
}
cout << dp[ w ] << endl;
find_path( n, w, 1 );
}






















 2027
2027

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








