Visual Odometry of Computer Vision 视觉里程计设计中的数学部分

最新推荐文章于 2024-06-21 17:14:10 发布

Luke Liu

最新推荐文章于 2024-06-21 17:14:10 发布

阅读量351

点赞数

分类专栏： Computer Vision 文章标签：算法计算机视觉

本文链接：https://blog.csdn.net/magicboom/article/details/113186548

版权

Computer Vision 专栏收录该内容

2 篇文章 0 订阅

订阅专栏

Visual Odometry of Computer Vision 视觉里程计设计中的数学部分

Principile Algorithm of Visual Odometry of Computer Vision ( Make sure You underStand LaTex )
Chrome Latex Extention is required, If Not, Please via:
https://blog.csdn.net/magicboom/article/details/113186548

Github Repo: https://github.com/Magicboomliu/VO

Some basic mathematical concepts 一些基本的数学概念

1.Camera Model 相机模型

假设P 的真实世界坐标为 $X,Y,Z]{^T}$ , 相机的成像坐标为 $X',Y',Z']{^T}$ , 焦距为 $f$ ,二者满足以下的关系:
$\frac{X}{Z}$
$\frac{Y}{Z}$
P像素坐标为 $u,v]{^T}$ , $u$ 、 $v$ 和 $X^{'}$ 、 $Y^{'}$ 之间又满足如下关系：
$\begin{cases} u =\alpha X' +c_x \\ u =\beta Y' +c_y \end{cases}$
令 $\alpha f = f_x, \beta f =f_y$ ,
$\begin{cases} u =f_x\frac{X}{Z} \\ v = f_y \frac{Y}{Z} \end{cases}$
以上的关系可以使用矩阵进行描述：
$\begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = \begin{bmatrix} &f_x,&0,&c_x\\ & 0,&f_y,&c_y\\ & 0,&0,&1\\ \end{bmatrix} \begin{bmatrix} X\\ Y\\ Z \end{bmatrix} = KP$
K记录为相机内参矩阵，Camera Matrix.
在现实世界中,P位置记录为 $P_w$ , $T$ 为变换矩阵：
$ZP_{uv} = Z \begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = K(RP_w+t) = KTP_w$
其中 $TP_w$ 为相机坐标系下的做坐标，一般为归一化坐标 $P_c$ ：
$P_c '= TP_w, = \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ \end{bmatrix}$
$P_c = Normal(TP_w) = \begin{bmatrix} X_c/Z\\ Y_c/Z\\ Z_c/Z\\ \end{bmatrix}$

2.Epipolar Geometry 对极几何

设第一个特征点为 $p 1$ ,第二个坐标点为 $p 2$ , 初始状态下相机Pose 为 0，
则满足：
$\begin{cases} x_1p_1 = KP \\ x_2p_2 =K(RP+t) \end{cases}$
令：
$\begin{cases}x_1 = K^{-1}p_1 \\ x_2 = K^{-1}p_2 \end{cases}$
则 $x_1$ ， $x_2$ 满足对极约束：（ram代表 Real antisymmetric matrix)
$x_2{^T}t_{ram} Rx_1=0$
如果用 $p_1$ ， $p_2$ 表示为： $p_2^{T}K^{-T}t_{ram} RK^{-1}p_1=0$

其中，记录 $E= t_{ram}R$ 为本质矩阵（Essential matrix）， $F= K^{-T}EK^{-1}$ 为基本矩阵。（Fundamental matrix）

补充：若三维向量 $a=\begin{bmatrix} a_1\\ a_2\\ a_3\\ \end{bmatrix}$ 那么a的反对称矩阵:

$a_{ram}=\begin{bmatrix} 0,&-a_3,&a_2\\ a3,&0,&-a_1\\ -a_2,&a1,&0\\ \end{bmatrix}$

VO的基本思路之一：根据匹配特征点算E,F, 根据E,F用SVD或是Bundle Adjustment算R,t.

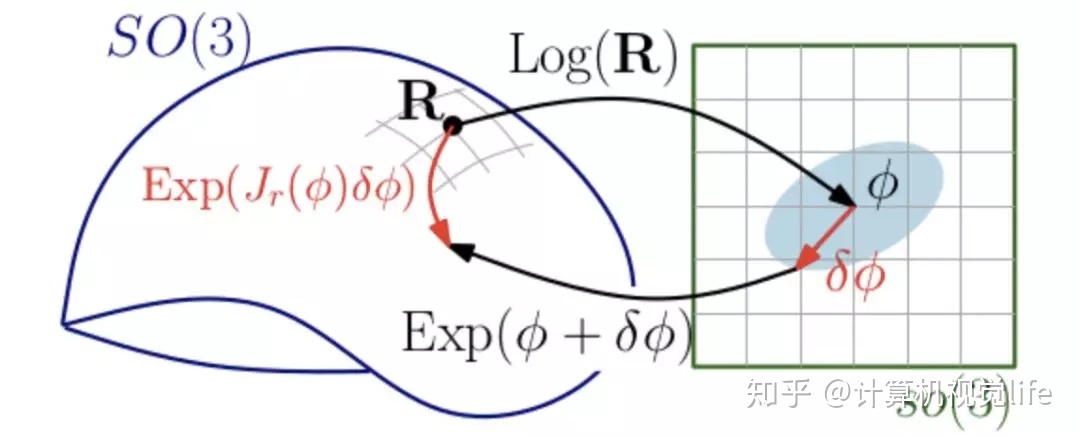
3 Lie algebra 李代数

李代数的存在是方便对旋转矩阵求微分，从而达到优化的效果。因为旋转矩阵本身不满足“群”的性质：比如一个旋转矩阵 $R_1$ 加上另外一个旋转矩阵 $R_2$ 不能保证为旋转矩阵，因此很难进行微分运算，因此我们把旋转矩阵映射到一个特殊的群上，使其能够满足进行微分运算的性质，这个群就是 “李群”。李代数对应李群的正切空间，它描述了李群局部的导数。

矩阵是可以微分的，矩阵对时间 $t$ 的微分为一个反对称(也叫斜对称)矩阵左乘它本身,对于某个时刻的R(t)（李群空间），存在一个三维向量φ=（φ1，φ2，φ3）（李代数空间），用来描述R在t时刻的局部的导数：

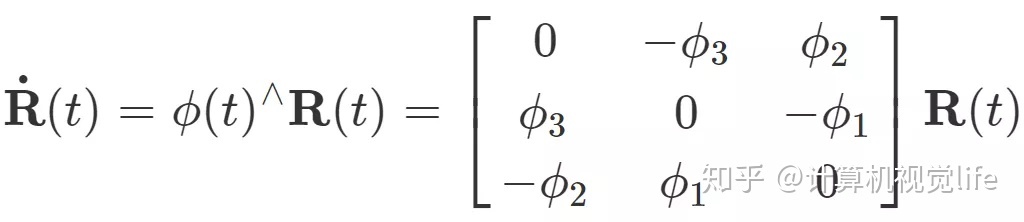
SO(3)上的原点 φ0 附近的正切空间上。这个φ正是李群大SO(3)对应的李代数小so(3), 即在原点附近，满足以下关系:

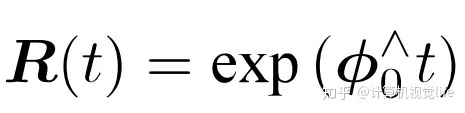
李代数小so(3)是三维向量φ的集合，每个向量φi的反对称矩阵都可以表达李群(大SO(3))上旋转矩阵R的导数，而R和φ是一个指数映射关系。

然后可以使使用Taylor公式对 $R (t)$ 进行计算：

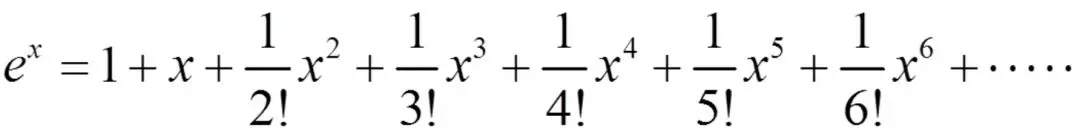
由此可以看出， so(3)本质上由旋转向量组成的的空间，这样我们可以说旋转矩阵的导数可以由其对应的旋转向量指定，指导如何在旋转矩阵中进行微积分运算。

SO(3) SE(3)和 so(3) se(3)的转换关系：

矩阵优化的思路：

李代数表示Pose,使用李代数加法求导。（李代数求导模型）
使用李代数左乘，右乘微小扰动，对该扰动求导。（扰动模型）

p为空间内部一点，R为Pose，我们对R求导。

（1）用李代数表示姿态，然后根据李代数加法来对李代数求导。即传统求导的思路，把增量直接定义在李代数上。

(2) 对李群SO（3）左乘或者右乘微小扰动，然后对该扰动求导，称为左扰动和右扰动模型。即把增量扰动直接添加在李群上，然后使用李代数表示此扰动。

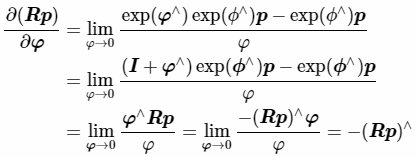
（3）SE(3)上面,含义是：考虑一个空间点P（需要是齐次坐标，否则维数不对），受到刚体变换T，得到TP：

上面最后一行矩阵除法，与矩阵乘法规则类似，只是乘号变成了除号。其使用一个4×1矩阵除以一个1×6矩阵得到一个4×6矩阵

引入李群李代数的意义：第一个是因为在欧式变换矩阵上不好定义导数，引入李群李代数使得导数定义变得自然合理；第二个是本来旋转矩阵与欧式变换矩阵具有本身的约束，使得将它们作为优化变量会引入额外约束，通过李群李代数可以使得问题变成一个无约束的优化问题（旋转变量有约束，因为旋转矩阵必须满足正交矩阵行列式为1，优化起来不方便）.

4. 非线性优化问题 Nonlinear optimization problem

不能保证特征点绝对准确，存在造成因素使得 $R$ ,$
t$求解出来不一定正确，因此需要Nonlinear optimization。

常见的方法有高斯-牛顿（Gausss-Newton）G-N法
列文伯格-马夸尔特（Levenburg-Marquatt）LM法

高斯-牛顿（Gausss-Newton）G-N法

假设优化函数为 $f (x)$ , 将该优化目标进行Taylor展开：
$f(x+\Delta x) = f(x)+ J(x)\Delta x$
求解最小2乘问题：
$\Delta x^* = argmin_{\Delta x^*} \frac{1}{2}\parallel {f(x)+J(x)\Delta x}\parallel ^2$
求解 $\Delta x$ 的导数使其为0.得到如下方程：
$J(x)^{T}J(X)\Delta x = -J(x)f(x)$
这个方程成为增量方程（Incremental equation), 也叫高斯牛顿方程（G-N equation,) 其中我们定义 $J(x)^{T}J(X)$ 为 H(近似于2阶导数，Hessian Matrix), $- J (x) f (x)$ 为 g（有些地方写成 b）, 则增量方程可以写成：
$H\Delta x = g$

现在给出G-N算法的流程：

给定初始值 $x_0$
计算此时的误差 $f(x_0)$ 和对应的J(x).
计算H和g
计算 $\Delta x$
Let $x_0 + \Delta x$
重新计算误差 $f(x_0)$ 和对应的J(x)，重复以上行为
当 $\Delta x$ 足够小，停止。

高斯-牛顿（Gausss-Newton）G-N法对应前段 $B u n d l e A d j u s t m e n t$

误差为重投影误差（Reprojection error）, 一般用于优化PnP问题或是ICP问题。
已知n个三维的空间点坐标P和投影p(像素坐标)，希望计算相机Pose 的 R 和 t, Pose 对应的se(3)为 $\xi$ , 则根据相机模型，满足如下关系:
$s_iu_i = K exp(\xi_{ram})P_i$
重投影误差计算为：
$\xi^*=argmin_{\xi}\frac{1}{2} \sum_{i=1}^{n} \parallel u_i -\frac{1}{s_i}K exp(\xi_{ram}) P_i \parallel ^2$
在优化前，首先我们需要知道每个点的3维度相机坐标系下坐标：
$exp(\xi_{ram}P)_{1:3} = [X' , Y', Z']$
这个可以根据相机模型去获得（根据相机坐标u ,v），因为：
$\begin{cases}u = f_x\frac{X'}{Z'} \\ v = f_y\frac{Y'}{Z'} \end{cases}$

使用G-N方法，解的的$J(x)为一个 2 x 6 的雅克比矩阵：
$\frac{\partial e}{\partial \delta\xi} = - \begin{bmatrix} \frac{f_x}{Z'}, &0,&-\frac{f_xX'}{Z'^2},& -\frac{f_xX'Y'}{Z'^2}, &f_x +\frac{f_xX^2}{Z'^2}, &-\frac{f_xY'}{Z'} \\ 0, &\frac{f_y}{Z'}, &-\frac{f_yY'}{Z'^2},&-f_y -\frac{f_yY'^2}{Z'^2}, &-\frac{f_yX'Y'}{Z'^2}, &-\frac{f_yX'}{Z'} \end{bmatrix}$
根据这个J(x)可以计算H，在根据H,f(x),J(x)计算 $\Delta \xi$ ，更新 $\xi$ ，从而更新R和t。
BA算法出来优化Pose之外，还可以优化点P的坐标得到的J(x)是一个2 x3 的矩阵：
$\frac{\partial e}{\partial P} = - \begin{bmatrix} \frac{f_x}{Z'}, &0,&-\frac{f_xX'}{Z'^2} \\ 0, &\frac{f_y}{Z'},&-\frac{f_yY'}{Z'^2} \end{bmatrix} R$
然后计算 $\Delta P$ ,更新P。
下面展示高翔博士用G-N 做BA求解R和t 的 C++ Code
$\begin{bmatrix} &f_x,&0,&c_x\\ & 0,&f_y,&c_y\\ & 0,&0,&1\\ \end{bmatrix}$
为相机内参K，第一步是// 将坐标转为相机坐标系下的坐标

// 将坐标转为相机坐标系下的坐标
Point2d pixel2cam(const Point2d &p, const Mat &K) {
  return Point2d
    (
      (p.x - K.at<double>(0, 2)) / K.at<double>(0, 0),
      (p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
    );
}

这里得到的Point2d其实是[ $\frac{X'}{Z'}$ , $\frac{Y'}{Z'}$ ], 可以理解为用 $Z^{'}$ 归一化的相机坐标系下的坐标。

接下来就是计算 $\xi$

void bundleAdjustmentGaussNewton(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose) {
  typedef Eigen::Matrix<double, 6, 1> Vector6d;
  const int iterations = 10;
  double cost = 0, lastCost = 0;
  double fx = K.at<double>(0, 0);
  double fy = K.at<double>(1, 1);
  double cx = K.at<double>(0, 2);
  double cy = K.at<double>(1, 2);

  for (int iter = 0; iter < iterations; iter++) {
    Eigen::Matrix<double, 6, 6> H = Eigen::Matrix<double, 6, 6>::Zero();  //这里之所以是 6 x 6 是因为J(x)TJ(X) = H, J(X)是2 x 6 
    Vector6d b = Vector6d::Zero(); // b = J(x)Tf(x), J(x)T是 6 x 2, f(x)是 x,y 2个维度的误差，所以是2 x 1.

    cost = 0;
    // compute cost
    for (int i = 0; i < points_3d.size(); i++) {
      Eigen::Vector3d pc = pose * points_3d[i];
      double inv_z = 1.0 / pc[2]; // 1/Z'
      double inv_z2 = inv_z * inv_z;  // 1/Z^2
      Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);

      Eigen::Vector2d e = points_2d[i] - proj;  // 重投影误差

      cost += e.squaredNorm();
      Eigen::Matrix<double, 2, 6> J;  // 可以直接套结论的矩阵
      J << -fx * inv_z,
        0,
        fx * pc[0] * inv_z2,
        fx * pc[0] * pc[1] * inv_z2,
        -fx - fx * pc[0] * pc[0] * inv_z2,
        fx * pc[1] * inv_z,
        0,
        -fy * inv_z,
        fy * pc[1] * inv_z2,
        fy + fy * pc[1] * pc[1] * inv_z2,
        -fy * pc[0] * pc[1] * inv_z2,
        -fy * pc[0] * inv_z;

      H += J.transpose() * J;  // n点累加
      b += -J.transpose() * e;
    }

    Vector6d dx;
    dx = H.ldlt().solve(b); // 更新 se3

    if (isnan(dx[0])) {
      cout << "result is nan!" << endl;
      break;
    }

    if (iter > 0 && cost >= lastCost) {
      // cost increase, update is not good
      cout << "cost: " << cost << ", last cost: " << lastCost << endl;
      break;
    }

    // update your estimation // 更新SE(3)
    pose = Sophus::SE3d::exp(dx) * pose; 
    lastCost = cost;

    cout << "iteration " << iter << " cost=" << std::setprecision(12) << cost << endl;
    if (dx.norm() < 1e-6) {  // 当需要更新的左乘se(3)足够小。
      // converge
      break;
    }
  }

  cout << "pose by g-n: \n" << pose.matrix() << endl;
}

在main （）函数中调用：

int main（int argc, char** argv）{
// ......前期求特征点或是三角测量 省略........
............
Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K);
pts_3d.push_back(Point3f(p1.x * dd, p1.y * dd, dd)); // dd为深度， 第一个图知道3D
pts_2d.push_back(keypoints_2[m.trainIdx].pt);  // 第2个图知道2d， 这个是3d-2d，问题

// 使用 P-n-P求解
Mat r, t;
  solvePnP(pts_3d, pts_2d, K, Mat(), r, t, false); // 调用OpenCV 的 PnP 求解，可选择EPNP，DLS等方法
  Mat R;
  cv::Rodrigues(r, R); // r为旋转向量形式，用Rodrigues公式转换为矩阵
  cout << "solve pnp in opencv cost time: " << time_used.count() << " seconds." << endl;
// 这是不用BA的解法
  cout << "R=" << endl << R << endl;
  cout << "t=" << endl << t << endl;

// 下面我们使用BA
 VecVector3d pts_3d_eigen;
  VecVector2d pts_2d_eigen;
  for (size_t i = 0; i < pts_3d.size(); ++i) {
    pts_3d_eigen.push_back(Eigen::Vector3d(pts_3d[i].x, pts_3d[i].y, pts_3d[i].z));
    pts_2d_eigen.push_back(Eigen::Vector2d(pts_2d[i].x, pts_2d[i].y));
  }

  cout << "Calling bundle adjustment by gauss newton" << endl;
  Sophus::SE3d pose_gn;
  bundleAdjustmentGaussNewton(pts_3d_eigen, pts_2d_eigen, K, pose_gn);
cout<<"T="<<endl<<pose_gn.matirx()<<endl;
}

Levenberg-Marquardt（列文伯格-马夸尔特）算法

LM方法在一定程度上修正了这些问题，一般认为它比GN更为鲁棒。尽管它的收敛速度可能比GN慢，被称之为阻尼牛顿法.由于GN中采用近似的二阶泰勒展开只能在展开点附近有较好的近似效果，所以我们很自然的想到应该给 $\Delta x$ 添加一个信赖区域(Trust Region)，不能让它太大使得近似不准确。非线性优化有一系列这类方法，这类方法也被称之为信赖区域方法(Trust Region Method)。在信赖区域里面，我们认为近似是有效的，出了这个区域，近似可能会出问题。

那么如何确认这个信赖区域的范围？一个比较好的方法是根据我们的近似模型跟实际函数之间的差异来确定。如果差异够小，我们让范围尽可能大。如果差异大，我们就缩小这个近似范围。因此，可以考虑使用

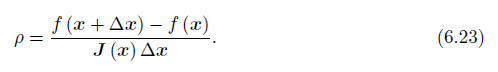
来判断泰勒近似是否够好，分子式实际函数下降的值，分母是近似模型下降的值。如果接近于1，则近似是好的。如果太小，说明实际减小的值远少于近似减少的值，这认为近似比较差。反之，如果比较大，则说明实际下降的比预计的更大，我们可以放大近似范围.

相当于一个带约束的最小2乘法：

最后可以得到增量方程：

记录 $D^TD = I$ ，简化增量方程：

我们看到，当参数 $\lambda$ 比较小时， $H$ 占主要地位，这说明二次近似模型在该范围内是比较好的，LM方法更接近于GN法。另一方面，当 $\lambda$ 比较大时， $\lambda I$ 占主要地位，LM更接近于一阶梯度下降法，这说明附近二次近似不够好。LM的求解方法可以一定程度避免线性方程组的系数矩阵非奇异和病态问题，提供更稳定更准确的增量 $\Delta x$ 。

伪代码逻辑：

补充：如何使用 G2O进行图优化

SLAM领域，基于图优化的一个用的非常广泛的库就是g2o，它是General Graphic Optimization 的简称，是一个用来优化非线性误差函数的c++框架。

G2O的基本框架如下：

G2O 本身的核心是一个稀疏矩阵的优化器。即图中的SparseOptimizer, 由图可知，它一个优化图OptimizableGraph，也是一个超图HyperGraph，这个超图包含了许多顶点（HyperGraph::Vertex）和边（HyperGraph::Edge）。而这些顶点顶点继承自 Base Vertex，也就是OptimizableGraph::Vertex，而边可以继承自 BaseUnaryEdge（单边）, BaseBinaryEdge（双边）或BaseMultiEdge（多边），它们都叫做OptimizableGraph::Edge。
在G2O中，顶点 Vertex 代表优化的对象，比如相机Pose(R,t)，而边 Edge 表示误差，即用来优化 Vertex 的量（如重投影误差)。

整个图的核心SparseOptimizer 包含一个优化算法（OptimizationAlgorithm）的对象。OptimizationAlgorithm是通过 OptimizationWithHessian 来实现的。其中迭代策略可以从Gauss-Newton（高斯牛顿法，简称GN）, Levernberg-Marquardt（简称LM法）, Powell’s dogleg 三者中间选择一个（我们常用的是GN和LM）

OptimizationWithHessian 内部包含一个求解器（Solver），这个Solver实际是由一个BlockSolver组成的。这个BlockSolver有两个部分，一个是SparseBlockMatrix ，用于计算稀疏的雅可比和Hessian矩阵；一个是线性方程的求解器（LinearSolver），它用于计算迭代过程中最关键的一步HΔx=−b，LinearSolver有几种方法可以选择：PCG, CSparse, Choldmod。

但是在写代码时候，我们需要从定义BlockSovler,LinearSolver开始写起：写G2O代码的逻辑步骤如下：

创建一个线性求解器LinearSolver。（解增量方程H△X=-b，可以制定解法）
创建BlockSolver。并用上面定义的线性求解器初始化
创建总求解器solver。并从GN, LM, DogLeg 中选一个，再用上述块求解器BlockSolver初始化
创建终极大boss 稀疏优化器（SparseOptimizer），并用已定义求解器作为求解方法。
定义图的顶点和边。并添加到SparseOptimizer中。
设置优化参数，开始执行优化。
具体每一个部分参考《一起动手SLAM》的文章, 介绍很详细：
G2O框架介绍
 G2O Vertex的定义方法
 G2O Edge的定义方法

Luke Liu

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
1
评论
Visual Odometry of Computer Vision 视觉里程计设计中的数学部分

Visual Odometry of Computer Vision 视觉里程计设计中的数学部分Principile Algorithm of Visual Odometry of Computer Vision ( Make sure You underStand LaTex )Github Repo: https://github.com/Magicboomliu/VOSome basic mathematical concepts 一些基本的数学概念Camera Model 相机模型假
复制链接

扫一扫