excel统计分析——一元直线回归

最新推荐文章于 2024-05-23 17:03:47 发布

maizeman126

最新推荐文章于 2024-05-23 17:03:47 发布

阅读量1.1k

点赞数 26

分类专栏： excel统计分析文章标签：回归数据挖掘统计分析 excel

本文链接：https://blog.csdn.net/maizeman126/article/details/136573126

版权

excel统计分析专栏收录该内容

62 篇文章 3 订阅

订阅专栏

参考资料：生物统计学

两个具有因果关系的协变量如果呈直线关系，可以用直线回归模型来分析两个变量的关系。直线回归（linear regression）是回归分析中最简单的类型，建立直线回归方程并经检验证明两个变量存在直线回归关系时，可以用自变量的变化预测因变量的变化。

1、回归方程的建立

（1）数学模型

设自变量为x，因变量为y，两个变量的n对观测值为(x1,y1)，(x2,y2)，...，(xn,yn)。可以用直线函数关系来描述变量x、y之间的关系：

$Y=\alpha +\beta x+ \varepsilon$

其中，α、β为待定系数，随机误差为 $\varepsilon \sim N(0,\sigma^2)$ 。设(x1,Y1)，(x2,Y2)，...，(xn,Yn)是取自总体(x,Y)的一组样本，而(x1,y1)，(x2,y2)，...，(xn,yn)是该样本的一组观测值，x1，x2，...，xn是随机取定的不完全相同的数值，而y1，y2，...，yn为随机变量Y在试验后取得的具体数值，则有：

$y_i=\alpha+\beta x_i+\varepsilon_i$

其中i=1,2，...，n，ε1，ε2，...，εn相互独立。该模型可理解为对于自变量x的每一个特定的取值xi，都有一个服从正态分布的Yi取值范围与之对应，这个正态分布的期望是α+βx，方差时σ^2。 $Y\sim N(\alpha+\beta x ,\sigma ^2)$ ， $E(Y)=\alpha+\beta x$ ，回归分析就是根据样本观察值求解α和β的估计值a和b。对于给定的x，有：

$\hat{y}=a+bx$

作为 $E(Y)=\alpha+\beta x$ 的估计，上式称为y关于x的直线回归方程，其图像称为回归直线，a称为回归截距（regression intercept），b称为回归系数（regression coefficient）。

（2）参数α、β的估计

在样本观测值(x1,y1)，(x2,y2)，...，(xn,yn)中，对每个xi都可由直线回归方程式确定一个回归估计值。即

$\hat{y_i}=a+bx_i$

这个归回估计值与机制观测值之差为：

$y_i-\hat{y_i}=y_i-(a+bx_i)$

表示yi与回归直线 $\hat{y}=a+bx$ 的偏离度。

为使建立的回归直线 $\hat{y}=a+bx$ 尽可能地靠近各观测值的点（xi,yi）（i=1,2,...,n），需使离回归平方和（或称剩余平方和） $Q=\sum_{i=1}^n(y_i-\hat{y_i})^2=\sum_{i=1}^n(\hat{y}-a-bx_i)^2$ 最小。

根据最小二乘法，要使Q最小，需求Q关于a、b的偏导数，并最终得到：

$a=\bar{y}-b\bar{x}$

$b=\frac{\sum((x-\bar{x}))(y-\bar{y})}{\sum(x-\bar{x})^2}=\frac{SP_{xy}}{SS_x}$

a和b为α和β的最小二乘估计。上式中，分子 $\sum(x-\bar{x})(y-\bar{y})$ 为x的离均差与y的离均差的乘积和，简称乘积和（sum of products），记作SP_xy；分母 $\sum(x-\bar{x})^2$ 为x的离均差平方和，简称平方和（sum of squares），记作SSx。

a为回归截距，是回归直线与y轴交点的纵坐标，是总体回归截距α的无偏估计值；b称为回归系数，是回归直线的斜率，是总体回归系数β的无偏估计值。回归直线具有以下性质：

①离回归的和等于零，即 $\sum_{i=1}^n(y_i-\hat{y_i})=0$ ；

②离回归平方和最小，即 $\sum_{i=1}^n(y_i-\hat{y_i})^2$ 最小；

③回归直线通过散点图的几何重心 $(\bar{x},\bar{y})$ 。

示例如下：

进行回归或相关分析前，为观察变量间关系的大致情况，一般先作散点图。

a，b的计算步骤如下：

2、回归的假设检验

即使x和y变量间不存在直线关系，有n对观测值（xi，yi）也可以根据上面介绍的方法求一个回归方程，所以回归方程建立后，需要进行假设检验来判断变量y与x之间是否确实存在直线关系。检验回归方程是否成立即检验假设 $H_0: \beta=0$ 是否成立，可采用F检验和t检验两种方法。

（1）回归方程的F检验

①平方和与自由度的分解

回归数据的总变异 $(y_i-\bar{y})$ 由随机误差 $(y_i-\hat{y_i})$ 和回归效应 $(\hat{y_i}-\bar{y})$ 两部分组成。如下图所示：

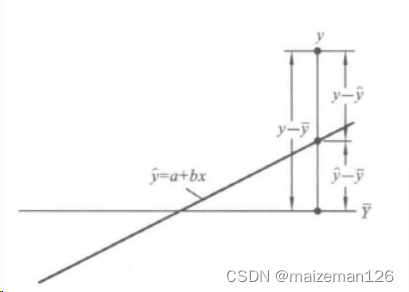
总平方和SSy可以分解为回归平方和SS_R及离回归平方和（误差平法和）SSe。各项的计算公式为：

$SS_y=\sum(y_i-\bar{y})^2$

$SS_R=\sum(\hat{y_i}-\bar{y})^2$

$SS_e=\sum(y_i-\hat{y_i})^2$

其中：

$SS_y=SS_R+SS_e$

$SS_R=\sum(\hat{y_i}-\bar{y})^2=\sum[(a+bx_i)-(a+b\bar{x})]^2$

$=b^2\sum(x_i-\bar{x})^2=b^2SS_x=b\frac{SP_{xy}}{SS_x}SS_x$

$=bSP_{xy}=\frac{SP_{xy}^2}{SS_x}$

$b^2SS_x$ 直接反映出y受x的线性影响二产生的变异，而 $bSP_{xy}$ 的算法则可以推广到多元线性回归分析。

SSy是因变量y的离均差平方和，所以自由度 $df_y=n-1$

SS_R反映有x引起的y的变异，所以自由度 $df_R=1$

SS_e反映除x对y的线性影响外的其他因素引起的y的变异，自由度 $df_e=n-2$

平方和与相应自由度的比为相应的均方，即：

$MS_R=\frac{SS_R}{df_R}=SS_R$

$MS_e=\frac{SS_e}{df_e}=\frac{SS_e}{n-2}$

②F检验

零假设 $H_0:\beta=0$

备择假设 $H_A:\beta\neq 0$

统计量F： $F=\frac{MS_R}{MS_e}$

和方差分析的F检验一样，回归方程的显著性F检验也总是使用回归均方做分子，离回归均方做分母。

本例的方差分析表如下：

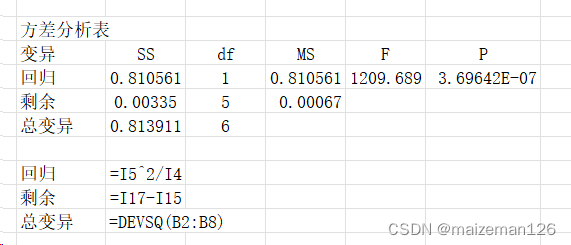
结论：p<0.01，说明本例存在线性回归关系，即求得的回归方程y=0.0137+0.8507x具有统计学上极显著的意义，是有效的。

（2）回归系数的t检验

对直线关系的检验也可以通过对回归系数b进行t检验完成。样本回归系数的变异度不仅取决于误差方差的大小，也取决于自变量x的变异程度。自变量x的变异越大（取值越分散），回归系数的变异就越小，有回归方程所估计出的值就越精确。

t检验的回归系数标准误为：

$s_b=\sqrt{s_b^2}=\sqrt{\frac{MS_e}{SS_x}}$

对回归系数t检验的假设为：

原假设： $H_0:\beta=0$

备择假设： $H_A:\beta\neq 0$

检验统计量t： $t=\frac{b-\beta}{s_b}=\frac{b}{s_b}$

统计量t服从df=n-2的t分布。

本例t检验如下：

对于一元直线归回而言，t检验与F检验是等价的，事实上 $F=t^2$

有时也对回归截距α的显著性进行检验。回归截距的大小对回归的显著性没有影响，检验的目的是看回归直线是否通过原点，仍使用t检验。检验时，零假设为α=0（回归直线通过原点），回归截距标准误：

$s_a=\sqrt{MS_e(\frac{1}{n}+\frac{\bar{x}^2}{SS_x})}$

统计量t：

$t=\frac{a-\alpha}{s_a}=\frac{a}{s_a}$

maizeman126

关注

26
点赞
踩
20

收藏

觉得还不错? 一键收藏
0
评论
excel统计分析——一元直线回归

即使x和y变量间不存在直线关系，有n对观测值（xi，yi）也可以根据上面介绍的方法求一个回归方程，所以回归方程建立后，需要进行假设检验来判断变量y与x之间是否确实存在直线关系。有时也对回归截距α的显著性进行检验。的估计，上式称为y关于x的直线回归方程，其图像称为回归直线，a称为回归截距（regression intercept），b称为回归系数（regression coefficient）。设自变量为x，因变量为y，两个变量的n对观测值为(x1,y1)，(x2,y2)，...，(xn,yn)。
复制链接

扫一扫