（C++）剑指offer-23：二叉搜索树的后序遍历序列（举例让抽象具体化）

剑指offer-23：二叉搜索树的后序遍历序列

目录

1问题描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

2二叉树遍历

二叉树的遍历有三种方式：

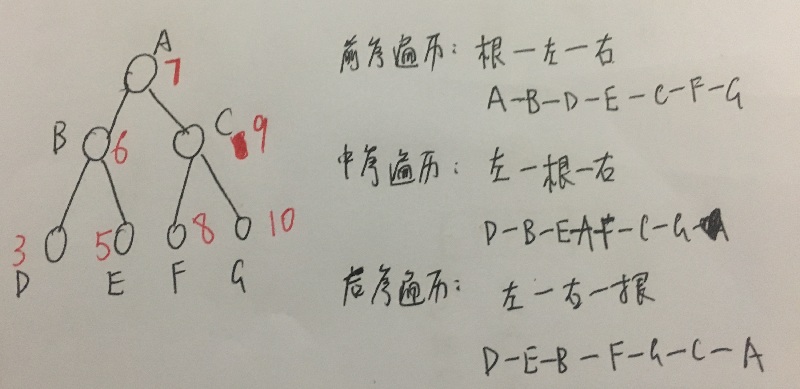
• 前序遍历（DLR）：首先访问根结点。然后如果有子树，则对于左孩子也采用DLR的遍历规则。没有就忽略。然后如果有右子树,则对右子树也采用DRL的遍历规则。没有就忽略。
• 中序遍历（LDR）：首先访问根节点的左子树（对左子树也采用LDR），没有则忽略。再访问根节点。最后则对右子树也采用LDR的遍历规则，没有就忽略。
• 后序遍历：首先访问根节点的左子树（对左子树也采用LRD），没有则忽略。再对右子树也采用LRD的遍历规则，没有就忽略。最后则对右子树也采用LRD的遍历规则，没有就忽略。

三种遍历方式其实是根据根节点的访问顺序命名的。根最先方位为前序，次之访问为中序遍历。最后访问为后序遍历。

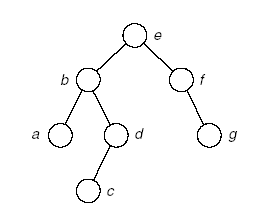
先序遍历图1的二叉树，结点的访问顺序为： e→b→a→d→c→f→g

中序遍历图1的二叉树，结点的访问顺序为：a→b→c→d→e→f→g

后序遍历图1的二叉树，结点的访问顺序为： a→c→d→b→g→f→e

3问题解析

BST的后序序列的合法序列是，对于一个序列S，最后一个元素是x （也就是根）
如果去掉最后一个元素的序列为T，那么T满足：

T可以分成两段，前一段（左子树）小于x，后一段（右子树）大于x，
且这两段（子树）都是合法的后序序列。完美的递归定义

4问题答案

（1）递归解法

class Solution {
public:
    bool VerifySquenceOfBST(vector<int> sequence) {
        if(sequence.size()==0) return false;
        return isLastOrder(sequence, 0, sequence.size()-1);
    }

private:
    bool isLastOrder(vector<int>& array, int left, int right){
        if(left >= right) return true; //相等叶子节点，大于是空树

        int mid = right;
        while(mid>left && array[mid-1]>array[right])
            --mid;  //找到左右孩子的分界点（mid为右孩子的第一个位置）

        for(int j=mid-1; j>=left; --j)
            if(array[j]>array[right])
                return false;

        return isLastOrder(array, left, mid-1) && isLastOrder(array, mid, right-1);
    }
};

（2）非递归，非递归也是一个基于递归的思想
左子树一定比右子树小，因此去掉根后，数字分为left，right两部分，right部分的
最后一个数字是右子树的根他也比左子树所有值大，因此我们可以每次只看有子树是否符合条件即可，即使到达了左子树左子树也可以看出由左右子树组成的树还向右子树那样处理
对于左子树回到了原问题，对于右子树，左子树的所有值都比右子树的根小可以暂时把他看出右子树的左子树
只需看看右子树的右子树是否符合要求即可

class Solution {
public:
    bool VerifySquenceOfBST(vector<int> sequence) {
        int size = sequence.size();
        if(0==size)return false;

        int i = 0;
        while(--size)
        {
            while(sequence[i++]<sequence[size]);
            while(sequence[i++]>sequence[size]);

            if(i<size)return false;
            i=0;
        }
        return true;
    }
};