机器学习总结（lecture 6）算法：主元分析PCA（无监督）

最新推荐文章于 2021-06-17 15:34:47 发布
最新推荐文章于 2021-06-17 15:34:47 发布
阅读量855 收藏 4
点赞数 1
分类专栏： 机器学习总结
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/malele4th/article/details/79342895
版权

lecture 6：主元分析PCA

目录

1PCA思想

  • PCA通过线性变换将原始数据，变换为一组各维度线性无关的表示

PCA通过原变量的线性组合，寻找一组能最大限度携带原变量的有用信息，且相互不相关的一组新变量，一般通过主元回归检验法、主元贡献率累积和百分比法来确定新变量个数，即降维后样本的维数。
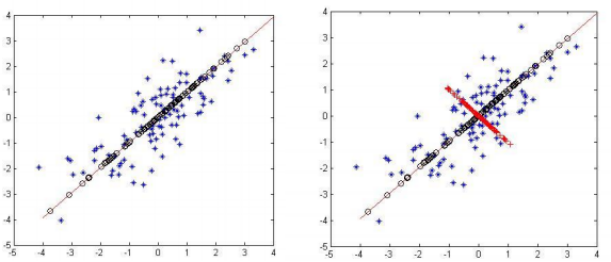
这里写图片描述
LDA与PCA的比较

（1）PCA与LDA非常类似，LDA输入数据带标签，是有监督的学习，LDA可以作为独立算法存在，给定训练数据得到判别函数，对数据预测。
（2）PCA输入数据不带标签，是无监督的学习，数据预处理方法，将原始数据降低维度，降维后的数据之间方差最大（投影误差最小）

有一组N维向量，降到K维（K 小于N），如何选择K个基，才能最大程度的保留原有信息
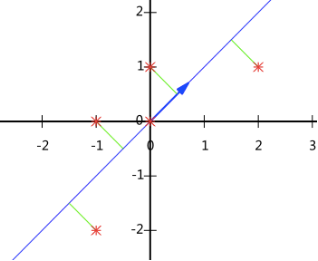
这里写图片描述
选择一个方向，所有数据投影到这个方向的直线上，用投影值表示原始记录，二维降到一维，希望投影后的投影值尽可能分散，寻找一组基，使得所有数据，变换为这个基上的坐标表示后，方差最大

2最大方差法

这里写图片描述

3PCA一般步骤

这里写图片描述
（1）数据预处理，消除数据在数量级和量纲上的差异，且进行零均值化
（2）m个n维样本，求出协方差矩阵 C=1mXXT C = 1 m X X T
（3）求出C的特征值，特征向量，将特征值排序
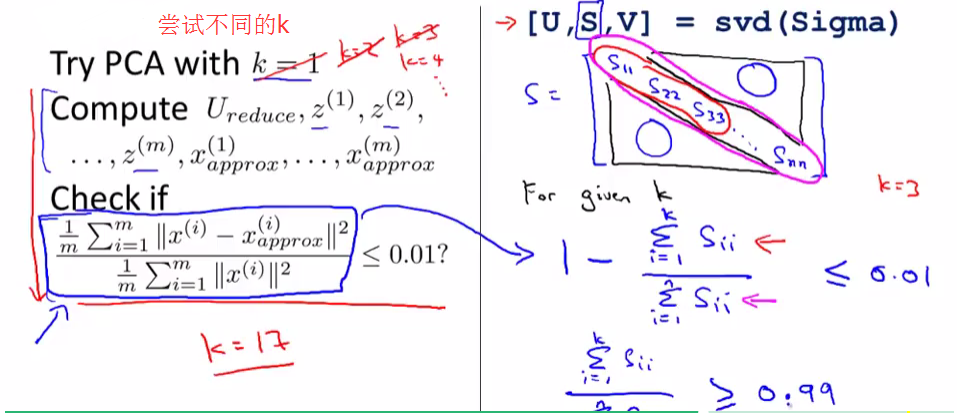
（4）选出前面最大的几个特征值，其和占所有特征值和的80%以上，找出对应的特征向量组成矩阵P
（5）Y=PX即为降维后的数据

4PCA协方差SVD分解

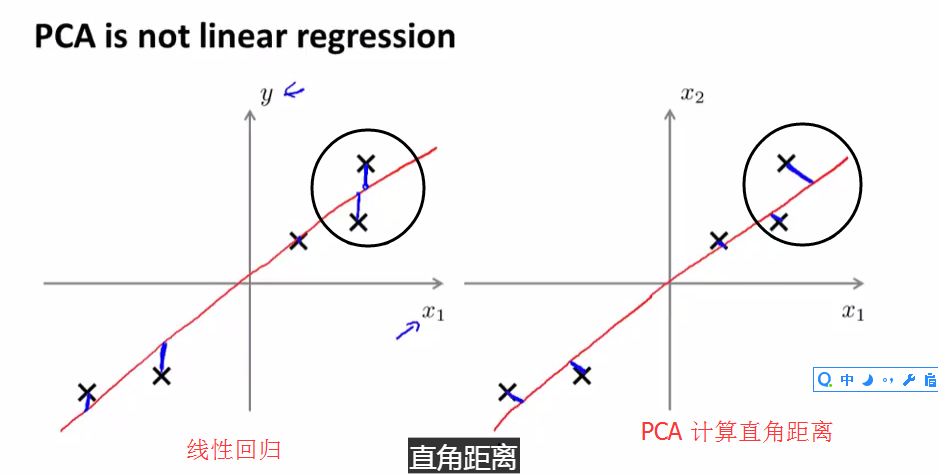
下面介绍线性回归与2维PCA的区别：虽然都是找一条直线去拟合但是计算loss的方式不同（垂直），PCA没有标签Y（非监督）。

  • PCA和LR是不同的算法，PCA计算的是投影误差，而LR计算的是预测值与实际值的误差。 PCA中只有特征没有标签数据y，LR中既有特征样本也有标签数据。

  • 求出协方差矩阵的特征值及对应的特征向量（使用svd函数）。
  • 特征向量最能代表原数据

这里写图片描述
这里写图片描述
SVD可以分解不是方阵的矩阵
这里写图片描述

九方先生
关注
专栏目录
【机器学习基础】无监督学习（1）——PCA
「 虚幻私塾」
01-22 1778
Python微信订餐小程序课程视频 https://edu.csdn.net/course/detail/36074 Python实战量化交易理财系统 https://edu.csdn.net/course/detail/35475 前面对半监督学习部分作了简单的介绍，这里开始了解有关无监督学习的部分，无监督学习内容稍微较多，本节主要介绍无监督学习中的PCA降维的基本原理和实现。 PCA 0.无监督学习简介 相较于有监督学习和半监督学习，无监督学习就是从没有标签的数据中进行知识发现的过程。 更具体地说，无
非监督学习——PCA
StevenJane
11-29 3592
PCA
机器学习导论（张志华）：主元分析
去向前方的博客
10-02 1166
前言 这个笔记是北大那位老师课程的学习笔记，讲的概念浅显易懂，非常有利于我们掌握基本的概念，从而掌握相关的技术。 basic concepts exp(−tz12)=∫exp(−tuz)dF(u)exp(-tz^{\frac{1}{2}}) =\int exp(-tuz) dF(u)exp(−tz21​)=∫exp(−tuz)dF(u) z=∣∣x∣∣2z=||x||^2z=∣∣x∣∣2 exp(...
无监督学习与主成分分析（PCA）
weixin_43580339的博客
06-17 3988
无监督学习与主成分分析（PCA）-降维 序 在之前的文章中，我讲了很多的监督学习的算法（线性模型，SVM，决策树，神经网络等），那么接下来，我们要开始接触无监督学习了。首先，我们先说下相关概念。 无监督学习 与监督学习不同，在无监督学习中，学习算法只有输入数据，并且从数据中提取需要的知识。而其中有两种常用类型：数据集变换和聚类。 无监督变换是创建数据新的表示的算法，与数据的原始表示相比，新的表示可能更容易被人或其它机器学习算法所理解。而无监督变换的一个常见应用就是降维，它接受包含许多特征的数据的高维表示，并
【机器学习】主成分分析 (PCA)、无监督特征提取
Gene_I must wait for the sunrise
01-07 1435
数据降维 主要有两类方法，用于将输入数据的特征降维，分别是「特征提取」与「特征选择」。 特征选择 在原始特征集中选择一个子集。 特征提取 对原始特征集中所有特征进行线性组合，实现降维的目的。通常分为无监督与有监督两类： 无监督：最小化信息损失 有监督：最大化类别间差异 PCA 特点：由于是无监督，因此降维时所有数据平等看待。 ...
斯坦福大学机器学习教程ppt（lecture6-lecture9），人工智能，机器学习必读经典课程。
01-30
常见的无监督学习任务包括聚类，如K-means算法，以及降维技术，如主成分分析（PCA）。此外，讲座可能还会讨论半监督学习和强化学习，它们是介于监督学习和无监督学习之间的方法，适用于标签数据有限的情况。 ...
ML-机器学习与量化交易项目：课件PPT+代码
最新发布
05-02
ML_机器学习与量化交易项目：课件PPT+代码 1. 课件PPT 2.代码 le cture_code 05 lecture_code 08 lecture_co de 04 lecture_code 03
斯坦福大学机器学习教程ppt（lecture10-lecture18），人工智能，机器学习必读经典课程。
01-30
6. **Lecture15**：可能涉及无监督学习，如聚类算法（K-means、DBSCAN）和降维技术（PCA、t-SNE），以及这些方法在数据探索和特征提取中的作用。 7. **Lecture16**：可能会讲解强化学习的基本概念，包括马尔科夫...
斯坦福大学机器学习教程ppt（lecture1-lecture5），人工智能，机器学习必读经典课程。
01-30
在第一讲中，Andrew Ng教授会介绍机器学习的基本概念，包括监督学习、无监督学习和强化学习的定义和区别。他会解释为什么机器学习如此重要，特别是在大数据时代。此外，还会讨论几种常见的机器学习问题，如回归、...
机器学习技法 Lecture6: Support Vector Regression
无所知的博客
12-04 1931
机器学习技法 Lecture6: Support Vector Regression1. Kernel Ridge Regression2. Support Vector Regression Primal3. Support Vector Regression Dual4. Summary of Kernel Models 1. Kernel Ridge Regression 先回忆一下之前讲的...
无监督学习-PCA
u012967763的专栏
01-24 1317
import numpy as np import matplotlib.pyplot as plt import pandas as pd #使用pandas分别读取训练数据和测试数据 digits_train = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits
（无监督数据降维）主成分分析法 - PCA
壮壮不太胖的学习笔记
05-15 1020
文章目录一，数学原理二，PCA的使用1，参数2，属性（方法）3，示例 SKlearn官网 - sklearn.decomposition.PCA 一，数学原理 参考：通俗易懂的主成分分析法（PCA）详解 二，PCA的使用 class sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_stat
（无监督）Python实现PCA算法（数据特征降维）(学习笔记)
maligebilaowang的博客
11-23 3567
一、前言 PCA算法算是一个比较简单的无监督机器学习算法。主要作用就是用作数据样本特征降维。个人对于PCA算法的理解是通过变换坐标系，从而将高维度样本压缩到低维度，同时还尽可能的保留样本数据的大部分信息。 PCA算法在实际项目应用中的作用包括以下几个方面： 用在数据预处理方面，在监督学习算法中，输入样本维度非常大的时候，此时为了加速学习算法可以利用pca算法降低样本维度，减小内存，提高运行效率。...
机器学习算法/模型——有监督到无监督（降维）：主成分分析（PCA）
Robin_Pi的博客
02-24 7112
主成分分析 PCA1. 背景：数据降维2. 主成分分析原理3. 求解主成分3.1 矩阵分解3.2 奇异值分解 1. 背景：数据降维 2. 主成分分析原理 3. 求解主成分 3.1 矩阵分解 3.2 奇异值分解 参考 机器学习数据预处理：数据降维之PCA 数据预处理：PCA原理推导 数据降维处理：PCA之特征值分解法例子解析 数据降维处理：PCA之奇异值分解（SVD）介绍 ...
李宏毅机器学习系列-无监督学习之PCA
王伟王胖胖的博客
08-26 1904
李宏毅机器学习系列-无监督学习之PCA无监督学习做什么聚类(Clustering)分布式表示(Distributed Representation)降维主成分分析 (Principle component analysis)数学推导 无监督学习做什么 我们做无监督学习一般就是两个方向，一个是降维，比如下面的树，只有输入，没有标签，我们希望通过一个函数抽象出少量的特征来描述他们，于是就抽出来了一个更...
非监督学习算法——PCA算法
Taiiiii的博客
05-01 704
文章目录PCA算法作用优缺点工作原理数学公式sklearn 调用PCA算法手打python实现简单PCA算法 PCA算法 作用 pca算法主要用于数据的降维，可以发现更便于人来理解的特征。还可以可视化，去噪。 数据降维的作用： 数据压缩 做数据可视化或特征提取（比如降到2维，看坐标图可视化） 异常值检测和聚类 优缺点 精度上可能稍微会有所丢失，但是速度上会提高 工作原理 工作原理：PCA找主成...
无监督学习之主成分分析PCA
Rocket,Qian的博客
08-19 1562
1.数据降维与主成分分析PCA 主成分分析（principal component analysis,PCA)是一种常用的无监督学习方法，利用正交变换把线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据，线性无关的变量称为主成分。 1.1 基本思想 后续持续补充，码公式不易！ 1.2 PCA算法 总结PCA算法步骤： 设有m条n维数据 将原始数据按列组成n行m列矩阵XXX 将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值 求出协方差矩阵C=1mXXTC={1\over m}
李宏毅机器学习（9）—无监督学习（PCA）
qq_37217397的博客
03-08 603
分类 无监督学习可以分为两类： 一类是化繁为简，实际上是聚类和降维； 另一类是无中生有，即生成算法。 聚类算法 下述两种算法的区别在于，K-means聚类要事先自己设定要划分为几个cluster，而HAC不需要。 K-means聚类 ①人工设定有k个cluster，并为他们设置K个随机的examples。 ②为所有的样本计算出他们最可能属于的cluster（计算距离）。 ③对每个cluster求m...
机器学习非监督分类之主成分分析（PCA）
fengziyihang的博客
04-09 2763
主成分分析是非监督分类中基础的算法，应用于降低特征的维度。在介绍主成分分析之前，我们要先介绍一下特征值和特征向量，因为在后面我们要用到。一、特征值和特征向量特征值如果有此时γ为矩阵A的特征值，对应的X为矩阵的特征向量。对于不相同的特征值，其特征向量是正交的。二、主成分分析算法：首先将X进行预处理；1、计算X的期望E（X）；2、计算D = E（x-E(x)）；3、计算xj = xj/Djj, 得到新...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值