（超简单、超易懂、超详细）算法精讲(四十八)： 快速傅立叶变换算法

        如果你也喜欢C#开发或者.NET开发，可以关注我，我会一直更新相关内容，并且会是超级详细的教程，只要你有耐心，基本上不会有什么问题，如果有不懂的，也可以私信我加我联系方式，我将毫无保留的将我的经验和技术分享给你，不为其他，只为有更多的人进度代码的世界，而进入代码的世界，最快捷和最容易的就是C#.NET,准备好了，就随我加入代码的世界吧！
一、算法简介

        快速傅立叶变换（Fast Fourier Transform，FFT）是一种高效的计算离散傅立叶变换（Discrete Fourier Transform，DFT）的算法。傅立叶变换是一种将信号从时域转换到频域的方法，用于分析信号的频率成分。

        FFT算法利用了离散傅立叶变换的对称性和周期性，通过将原始信号分解为多个较小规模的DFT并组合求解，从而大大降低了计算复杂度。

具体来讲，FFT算法的步骤如下：

1. 将输入信号序列分为偶数索引和奇数索引两部分，分别进行FFT。

2. 对两部分的结果进行合并，得到整个信号的FFT结果。

3. 递归地继续分解上述两部分，直到每个部分只包含一个元素，完成递归。

4. 最后将每个部分的结果按照规则合并，得到最终的FFT结果。

        由于FFT算法的时间复杂度为O(NlogN)，其中N是信号序列的长度，远远快于直接计算DFT的时间复杂度O(N^2)，所以FFT算法广泛应用于信号处理、图像处理、通信等领域。

        需要注意的是，FFT算法要求输入信号的长度为2的幂次方，因此在实际应用中，有时需要对输入信号进行补零或截断操作以满足该要求。

二、为什么要学习快速傅立叶变换算法：

        2.1 FFT算法是一种高效的算法，用于将时域信号转换为频域信号

        FFT算法的时间复杂度为O(nlogn)，比直接计算傅立叶变换的O(n^2)要快很多。因此，学习FFT算法可以帮助我们更高效地处理信号和数据，提高计算效率。

        2.2 FFT算法在许多领域都有应用

        FFT算法可以应用于图像处理、音频处理、通信系统、信号分析等许多领域。因此，学习FFT算法可以帮助我们更好地理解和应用这些领域的相关知识和技术。

        2.3 FFT算法是其他许多算法的基础

         很多算法和技术都依赖于FFT算法，例如数字滤波器设计、信号压缩、频谱估计等。因此，学习FFT算法可以为我们后续学习和应用这些算法提供基础。

        2.4 学习FFT算法可以帮助我们更好地理解傅立叶变换的原理和性质

        傅立叶变换是一种非常重要的数学工具，广泛应用于信号处理、图像处理、信号分析等领域。学习FFT算法可以帮助我们更好地理解傅立叶变换的概念、性质和应用。

三、快速傅立叶变换算法在项目中有哪些实际应用：

        3.1 信号处理

        FFT广泛应用于信号处理领域，可以用于频谱分析、滤波、降噪、频率识别等。例如，在音频处理中，FFT可以用于音频信号的频谱分析和音频特征提取。

        3.2 图像处理

        FFT可以用于图像的频域分析和滤波处理。例如，可以使用FFT对图像进行高通或低通滤波，以去除噪声或增强图像的某些特征。

        3.3 无线通信

        FFT广泛应用于无线通信系统中的频谱分析和信道估计。在OFDM（正交频分复用）系统中，FFT用于将频域数据转换为时域数据，并且在接收端进行反向转换。

        3.4 视频压缩

        在视频压缩中，FFT可以用于对视频序列进行频域变换，以便实现高效的压缩编码算法，例如基于DCT的JPEG压缩算法。

        3.5 语音识别

        FFT可以用于语音信号的频谱分析和特征提取，用于语音识别系统中的声学建模。

        3.6 数字滤波器设计

        FFT可以用于数字滤波器的设计和分析。通过将滤波器的频率响应转换到频域进行分析，可以更好地理解系统特性并进行优化。

        3.7数据压缩

        FFT在数据压缩算法中起到重要作用。例如，基于FFT的算法可以实现无损压缩或有损压缩，如MP3音频压缩和JPEG图像压缩。

四、快速傅立叶变换算法的实现与讲解：

        4.1 快速傅立叶变换算法的实现

                算法实现

  // 将复数数组转换为字符串表示形式，便于打印输出
  private static string ComplexArrayToString(Complex[] array)
  {
      string result = "";
      for (int i = 0; i < array.Length; i++)
      {
          result += array[i] + " ";
      }
      return result;
  }

  // 获取最接近的2的次幂
  private static int GetNextPowerOfTwo(int n)
  {
      int power = 1;
      while (power < n)
      {
          power *= 2;
      }
      return power;
  }

  // 填充数组到最接近的2的次幂，并用0填充剩余部分
  private static Complex[] PadArray(Complex[] array, int n)
  {
      Complex[] paddedArray = new Complex[n];
      for (int i = 0; i < n; i++)
      {
          if (i < array.Length)
          {
              paddedArray[i] = array[i];
          }
          else
          {
              paddedArray[i] = Complex.Zero;
          }
      }
      return paddedArray;
  }

  // 傅立叶变换
  public static Complex[] FFT(Complex[] array)
  {
      int n = array.Length;

      // 如果数组长度不是2的次幂，则填充数组
      int power = GetNextPowerOfTwo(n);
      Complex[] paddedArray = PadArray(array, power);

      // 递归基本情况，当数组只有一个元素时返回
      if (paddedArray.Length == 1)
      {
          return paddedArray;
      }

      // 定义奇偶数组
      Complex[] even = new Complex[paddedArray.Length / 2];
      Complex[] odd = new Complex[paddedArray.Length / 2];

      // 将数组元素分成奇偶部分
      for (int i = 0; i < paddedArray.Length; i++)
      {
          if (i % 2 == 0)
          {
              even[i / 2] = paddedArray[i];
          }
          else
          {
              odd[i / 2] = paddedArray[i];
          }
      }

      // 递归调用FFT函数计算奇偶数组的傅立叶变换
      Complex[] evenTransformed = FFT(even);
      Complex[] oddTransformed = FFT(odd);

      // 计算结果数组
      Complex[] transformed = new Complex[paddedArray.Length];

      // 计算傅立叶变换的结果
      for (int k = 0; k < n / 2; k++)
      {
          Complex twiddle = Complex.Exp(-2 * Math.PI * k * Complex.ImaginaryOne / n);
          transformed[k] = evenTransformed[k] + twiddle * oddTransformed[k];
          transformed[k + n / 2] = evenTransformed[k] - twiddle * oddTransformed[k];
      }

      return transformed;
  }

                算法调用

 public static void Main(string[] args)
 {
     // 定义一个复数数组
     Complex[] array = new Complex[] { 1, 2, 3, 4, 5, 6, 7, 8 };
     // 打印原始数组
     Console.WriteLine("原始数组: " + ComplexArrayToString(array));
     // 计算傅立叶变换
     Complex[] transformedArray = FFT(array);
     // 打印傅立叶变换结果
     Console.WriteLine("变换结果: " + ComplexArrayToString(transformedArray));
 }

                输出结果

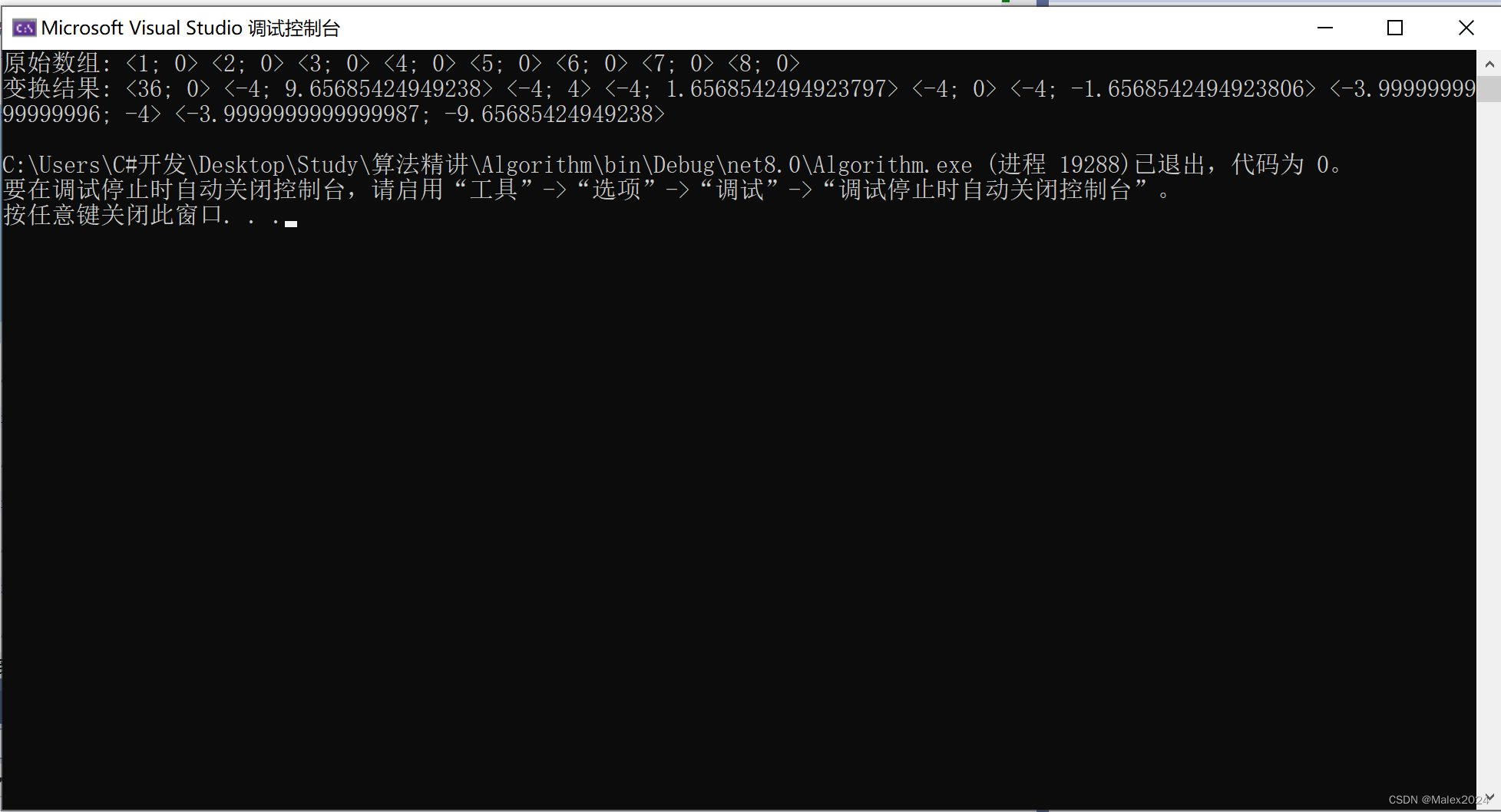
        4.2 快速傅立叶变换算法的讲解

  FFT方法是一个递归算法，它将输入的复数数组按照奇偶分成两个部分，并分别递归调用自己来计算这两个部分的傅立叶变换。然后，根据计算的结果，通过蝶形运算的方式计算整个数组的傅立叶变换。

        在Main方法中，定义了一个输入数组array，表示要进行傅立叶变换的原始数据。然后，调用FFT方法计算傅立叶变换，并将结果输出到控制台。

        在运行示例代码时，输出会显示原始数组和计算出的傅立叶变换结果。请注意，这个示例只是一个简单的示例，实际的傅立叶变换可能涉及到更复杂的数据处理和数学运算。

五、快速傅立叶变换算法需要注意的地方

        5.1 输入数据长度

        FFT算法要求输入的数据长度必须是2的幂。如果输入数据长度不是2的幂，则需要进行补零或截断等处理，以满足算法的要求。

        5.2 原始数据的顺序

        FFT算法要求输入数据按照特定的顺序排列。通常情况下，输入数据需要按照“自然排序”进行排列，即按照从低频到高频的顺序排列。

        5.3 复数运算

        FFT算法使用复数运算，需要使用复数的加减乘除等操作。在实现FFT算法时，需要确保对复数运算进行正确的处理。

        5.4 频谱结果的表示

        FFT算法的输出是频域的表示，即频谱。频谱通常以复数形式表示，其中实部表示幅度，虚部表示相位。根据具体的应用需求，可能需要对频谱进行进一步处理，如计算功率谱密度等。

        5.5 采样率和频率分辨率

        FFT算法可以用于获得信号的频谱信息，但要注意采样率和频率分辨率的关系。采样率表示每秒采集到的样本数，频率分辨率表示频谱中两个不同频率之间的最小间隔。频率分辨率等于采样率除以数据长度。

        5.6 窗函数的选择

        在进行FFT计算之前，通常需要对原始数据进行窗函数处理。窗函数有助于减小频谱泄露，并改善频谱的分辨率。常用的窗函数有汉宁窗、汉明窗等。