用遗传算法加强足球游戏的人工智能

最新推荐文章于 2023-11-07 17:51:14 发布

maliang1225

最新推荐文章于 2023-11-07 17:51:14 发布

阅读量1.6k

点赞数

分类专栏：数据结构和算法设计文章标签：算法游戏 iterator class 生物 vector

数据结构和算法设计专栏收录该内容

10 篇文章 0 订阅

订阅专栏

项目背景

一直都想用遗传算法（Genetic Algorithms）实现足球游戏的人工智能，但因为实现一个足球游戏的对战平台太过于繁琐而没有动手。直到在《Programming Game AI by Example》一书中看到一个SimpleSoccer的demo（以下简称demo），实现了一个red-blue两队进行机器与机器对抗的简单足球游戏。在读过它的源码之后，我决定在demo上进行二次开发——为它加入遗传算法，实验遗传算法在实时战略游戏（RTS）性质的体育游戏中的威力。

demo的架构非常好，采用了状态机来实现游戏流程，并分开计算游戏决策。因此加入遗传算法非常容易，只要在原来的状态机中增加一两个状态即可。red-blue两个队伍相互对抗，每队有五位球员，其中一位是守门员。这个demo的足球规则是简化的，除了只有五个球员外，没有手球也没有越位等规则，甚至连边界球都没有——球碰到边界就反弹回球场。简化的规则有利于我们简化实验的过程，不必把很多精力花费在过于复杂的规则上。

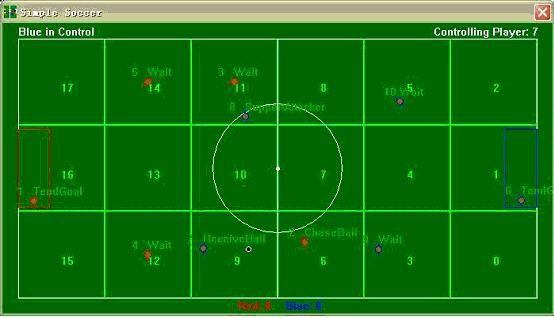
图一

在demo的实现中，球场被分割为18块大小相等的区域（见图一）。每一个球员都一个属于自己的区域（称为HomeRegion），如图一中blue队的10号在自己的HomeRegion(Region5)中处于Wait状态（球员的状态之一）。当一个球员不处于进攻状态（Attacking）、助攻（SupportAttacker）、逐球（ChaseBall）、运球（Dribble）、踢球（KickBall）及返回（ReturnToHomeRegion）时，他就进入Wait状态——等待球队发出的下一个行动指令。显然，就像人类进行足球比赛时需要排兵布阵一样，demo中球员站在哪个位置也相当重要，能否组织起有效的进攻或者防守，决定因素之一就是在合适的位置有没有球员可以快速有效地执行命令。在书中自带的demo中，球员的站位都是固定的，因此难以组织有效的进攻和防守，在某一时间段内容易形成一边倒的局势。使用遗传算法来对球员的站位进行决策分析，可以找出对当前局势就有利的位置编排方案。从而使得球队与球队之间的对抗趋于激烈、策略更加有效、攻守都更精彩。

遗传算法概述

遗传算法因为它在解决许多生产、生活中的问题上的卓越性能而经久不衰。随着计算机的计算能力日益增强和玩家对游戏中的人工智能的强烈需求，目前在单机游戏中已经开始应用遗传算法、人工神经网络等现代优化计算方法来增强游戏中的人工智能，并且形成了趋势。可见以后为加强机器的对抗性能，遗传算法、人工神经网络等都会越来越多地应用到游戏中。

遗传算法是模拟自然界中的生物对自然界的适应而不断进化这一客观事实的算法。为了解决某一个问题，在遗传算法中，我们虚拟一个物种（即解的表现形式或者称为解的编码），并将其放到“自然环境”中天下繁殖、进化，根据优胜劣汰、适者生存的自然法则，繁衍若干代之后，种群中的佼佼者将非常适应“自然环境”，这个佼佼者就是我们求得的解了。关于生物学与遗传算法之间的概念的对应关系可以用表一的形式来表示：

生物遗传概念	遗传算法中的作用
适者生存	在算法停止时，最优目标值的解有最大的可能性被留住
个体	解
染色体	解的编码(二进制形式或者十进制形式的串即向量，或者字符串)
基因	解中每一分量的特征(如各分量的值)
适应性	适应函数的返回值
群体	选定的一组解(其中解的个数为群体的规模)
种群	根据适应函数选取的一组解
交配	通过交配原则产生一组新解的过程
变异	编码的某一分量发生变化的过程

表一

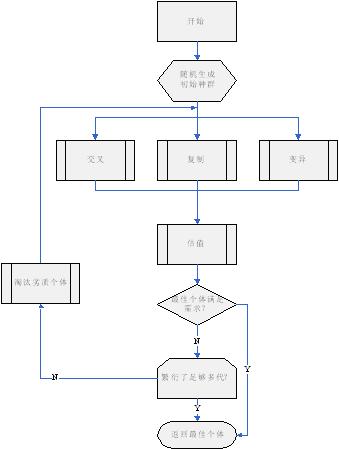
遗传算法的流程图如图二所示：

图二

遗传算法运行时，先生成初始群体（通常是随机产生一定数量的个体，这个数量就是群体的大小）；然后让群体繁殖下一代，繁殖的方式有交叉、复制和变异；经过繁殖后群体的数量增加，然后使用评估模块对每一个个体进行评估；如果群体中最佳个体已经足够优秀，那就跳出循环，返回最佳个体；否则判断是否已经繁殖了预定的代数，如果是就返回最佳个体，如果不是则淘汰一部分劣质个体并进入下一轮繁殖循环直至结束。

在遗传算法的实现中，最重要的主要有三点：一是染色体的编码，即一个新物种怎么样来表示它，通常染色体是问题的一个可能解的特定格式的表示，通常以二进制或者十进制的方式编码；二是为染色体实现交叉、复制、变异等算子；三是估值模块的编写。下面以这三点为中心，谈谈demo中的遗传算法实现。

染色体编码

染色体编码的方式有很多种，常见的是二进制方法和十制字方式，也有字符串方式的。如著名的旅行商问题(TSP)里，假设有20个城市以[0…19]编码，那么[7，6，9，8…19，3，0，4]这个包含20个元素的序列A就可以看作是一个染色体，每一个元素Aj(0<=j<20)就是染色体的一个基因。这个染色体可以解码为从编号为7的城市出发，到达城市6、城市9等等，最后到达城市4完成20个城市的遍历。显然，这个序列是TSP的一个可能解，因此染色体就是问题的可能解的表示方式。回到我们的足球游戏中来，我们期望获得某一队的球员的合适站位，那么如果我们把四个球员以[0…3]编号(因为守门员不应离开禁区所以不必考虑他的位置)，那序列B[14，11，12，6]就是一个站位方案，表示0号球员站在ID为14的Region中，1号球员站在ID为11的Region中，等。序列B叫做一个可能解，序列B的编码方式即是我们染色体的编码方式——十进制编码方式的一个序列。依照这个规则，我们编写代码如下：

typedef unsigned int Genetype;

class Chromosome{

private:

std::vector<Genetype> m_Geneme;

int m_iScore;

public:

Chromosome();

~Chromosome(){};

const std::vector<Genetype>& GetGeneme()const{return m_Geneme;}

void SetScore(int iScore){m_iScore = iScore;}

friend void Intercross(const Chromosome& p1, const Chromosome& p2,

Chromosome& c1, Chromosome& c2);

friend void Agamogenesis(const Chromosome& p, Chromosome& c);

friend void Mutant(const Chromosome& p, Chromosome& c);

friend class GT;

};

class GT{

public:

inline bool operator()(const Chromosome* c1, const Chromosome* c2)const{

return c1->m_iScore > c2->m_iScore;

}

};

类Chromosome是染色体封装，它的成员变量m_Geneme是一个基因序列，用std::vector容器来保存；成员变量m_iScore是这个染色体对“自然环境”的适应值，由评估模块评定。友元类GT实现了两个Chromosome的大小比较；还定义了三个友元函数分别实现交叉、复制及变异三个遗传算子，详见下节。

遗传算子

交叉、复制和变异三个遗传算子是遗传算法能够找到最优解的途径。这三个遗传算子模拟了自然界的物种交配和生殖的方式，为产生新的可行解提供了有效手段(见表一)。遗传算子声明为染色体类Chromosome的友元函数是为了方便操作它的私有变量，实现如下：

void Intercross(const Chromosome& p1, const Chromosome& p2,

Chromosome& c1, Chromosome& c2){

unsigned int IntercrossPoint = RangeRandom<unsigned int>(0, GeneLen);

unsigned int i = 0;

for(; i < IntercrossPoint; ++i){

c1.m_Geneme[i] = p1.m_Geneme[i];

c2.m_Geneme[i] = p2.m_Geneme[i];

}

for(; i < GeneLen; ++i){

c1.m_Geneme[i] = p2.m_Geneme[i];

c2.m_Geneme[i] = p1.m_Geneme[i];

}

void Agamogenesis(const Chromosome& p, Chromosome& c){

c.m_Geneme = p.m_Geneme;

}

void Mutant(const Chromosome& p, Chromosome& c){

unsigned int MutantPoint = RangeRandom<unsigned int>(0, GeneLen);

Genetype NewGene = RangeRandom<Genetype>(0,18);

c.m_Geneme = p.m_Geneme;

c.m_Geneme[MutantPoint] = NewGene;

}

Intercross，Agamogenesis和Mutant三个函数分别对应交叉、复制和变异三个遗传算子。Intercross函数传入两个Chromosome的实例，随机选择一点进行交叉，组成两个新的染色体用作返回值。Agamogenesis函数传入一个Chromosome实例，返回一个相同的染色体，以保证优势的种群可以壮大，从而使得遗传算法可以在有限的运行时间内收敛。Mutant函数传入一个Chromosome实例，随机选择一个元素（分量）赋以一个随机的Region ID，返回这一改变后的染色体，变异可以使得遗传算法跳出局部最优，趋近全局最优。三个遗传算子的操作结果如表二所示：

遗传算子	输入的染色体	输出的染色体
Intercross	[17,9,4,3] [16,13,7,9]	[17,9,7,9] [16,13,4,3] 假定元素2为交叉点
Agamogenesis	[17,9,4,3]	[17,9,4,3]
Mutant	[17,9,4,3]	[17,9,7,3] 假定元素2为变异点

表二

估值模块

通俗一点说，估值模块就是阎罗王，个体淘汰与否就得看估值模块的脸色了。估值模块判定每一个染色体对“自然环境”的适应度：如前文关于TSP的染色体，它的估值函数就返回遍历20个城市要走过的路程的总长度，总长度越短的染色体适应度越高，反之则越低。在足球游戏中，估值模块就没有这么简单了，一个染色体就是一个站位组合，这个组合的优劣是与当前局势有很大关系，如球的位置、对方球员的站位、已方球员的站位和控球权等有关，综合以上各种因素，编写如下估值模块：

int Environment:: Evaluate (const std::vector<Genetype>& candidate){

int iValue = 0;

for( unsigned int i = 0; i < GeneLen; ++i){

//减去移动需要的损耗

iValue -= DistOfTwoRgn(candidate[i], m_CurrGeneme[i]) * m_pPrm->CrossCostPerRgn;

//有利于防守？

iValue += GetDefendValue(candidate[i], m_OppGeneme);

//有利于进攻？

iValue += GetAttackValue(candidate[i], m_OppGeneme);

//有利于抢球或者保球？

if(m_iTeamColor == m_iControllingTeam

&& m_iBallRgnIdx == candidate[i])

iValue += m_pPrm->PlyrKeepBallValue;

else if(m_iTeamColor != m_iControllingTeam

&& m_iBallRgnIdx == candidate[i])

iValue += m_pPrm->PlyrChaseBallValue;

}

return iValue;

}

int Environment::GetDefendValue(const int iPlyrIdx, const std::vector<Genetype>& OppGeneme){

int iValue = 0;

int OppInMyGround = 0;

std::vector<Genetype>::const_iterator ci = OppGeneme.begin();

for(; ci != OppGeneme.end(); ++ci){

if(IsInMyGround(*ci))

++OppInMyGround;

}

if(OppInMyGround > 1 ){

if(IsInMyGround(static_cast<unsigned int>(iPlyrIdx)))

iValue += m_pPrm->DefendValuePerPlyr;

else

iValue += m_pPrm->DefendValuePerPlyr * 0.5;

}

else{

iValue += m_pPrm->DefendValuePerPlyr * 0.8;

}

if(m_iControllingTeam == m_iTeamColor)

iValue *= 1.2;

else

iValue *= 0.8;

return iValue;

}

int Environment::GetAttackValue(const int iPlyrIdx, const std::vector<Genetype>& OppGeneme){

int iValue = 0;

int OppNoInMyGround = 0;

std::vector<Genetype>::const_iterator ci = OppGeneme.begin();

for(; ci != OppGeneme.end(); ++ci){

if( !IsInMyGround(*ci))

++OppNoInMyGround;

}

if( OppNoInMyGround > 2 ){

if(IsInMyGround(static_cast<unsigned int>(iPlyrIdx)))

iValue += m_pPrm->AttackValuePerPlyr * 0.5;

else

iValue += m_pPrm->AttackValuePerPlyr;

}

if(m_iControllingTeam == m_iTeamColor)

iValue *= 1.2;

else

iValue *= 0.8;

return iValue;

}

Evaluate函数主要从以下几方面来对染色体进行评估：

·从当前位置到目的位置所要经过的路径的代价

·是否有利于进攻或者防守

·是否有利于持球或者抢球

其中计算是否有利于进攻或者防守是通过计算两个球队间球员的位置来判断的：对方的球员在已方半场时如果已方球员的目的位置也在已方半场就有利于防守；对方的球员在已方半场时如果已方球员的目的位置在对方半场则有利于进攻。通过这一简单的估值模块，可以使得遗传算法在淘汰劣质个体时有法可依，从而能够收敛得到较优解。通过精细化估值模块考虑更多因素（如对方球队可能采取的策略等）可使遗传算法的收敛速度加快，在真实的游戏项目中必定会使用精细化的估值模块的。

程序架构

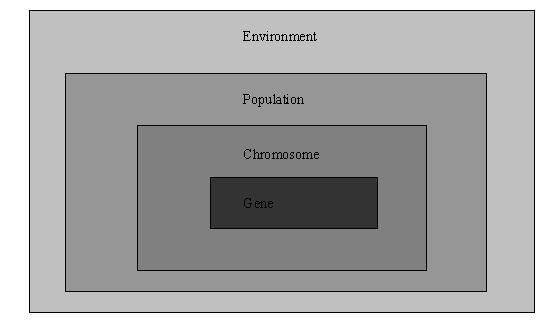
确定了遗传算法的编码方式、实现了三个遗传算子和估值模块之后，这个遗传算法基本上就完成了。但我们还没有看到它是怎么初始化种群、怎么繁殖和怎么淘汰劣质个体的，这时候有必要了解一下遗传算法的程序架构。在demo中，我们设计的遗传算法的架构如图三：

Environment

Population

Chromosome

Gene

图三

Environment是自然环境的模拟，它实现了估值函数、繁殖迭代的控制和环境的初始化和销毁等功能，最重要的是它包含了一种成员变量——Population的实例。每一个Environment还有一个算法参数包装类ParamLoader的实例指针m_pPrm用以存取配置文件。每一个球队拥有一个Environment实例，专门用以计算适合本队的球员位置编排。简化的Environment的声明如下：

class Environment{

private:

ParamLoader* m_pPrm;

Population m_Population;

private:

int Evaluate(const std::vector<Genetype>& candidate);

int GetDefendValue(const int iPlyrIdx, const std::vector<Genetype>& OppGeneme);

int GetAttackValue(const int iPlyrIdx, const std::vector<Genetype>& OppGeneme);

bool IsInMyGround(unsigned int iRgnIdx)

double DistOfTwoRgn(unsigned int iRgnIdx1, unsigned int iRgnIdx2)

public:

const std::vector<Genetype> GetBestGeneme();

};

当调用GetBestGnenme()时，遗传算法便开始运行，GetBestGeneme()控制繁殖迭代的次数，并挑选最优的染色体个体，它的实现如下：

const std::vector<Genetype> Environment::GetBestGeneme(){

for(unsigned int i = 0; i < m_pPrm->GAGeneration; ++i){

m_Population.NexGeneration();

unsigned int uiPopulationSize = m_Population.GetPopulationSize();

for(unsigned int i = 0; i < uiPopulationSize; ++i){

int score = Evaluate(m_Population.GetGenemeByID(i));

m_Population.SetScoreByID(i, score);

}

m_Population.KeepColonySize(m_pPrm->ColonySize);

}

return m_Population.GetBestGeneme();

}

Population是物种群体的抽象，它实现一个最重要的函数就是NextGeneration()，Environment通过调用这个函数让群体执行繁殖任务；另一个重要的函数就是KeepColonySize()，这个函数淘汰掉劣质的个体，让竞争力较强的个体进入下一轮繁殖。简化的Population声明如下：

class Population

{

private:

std::vector<Chromosome*> m_Colony;

unsigned int m_iColonySize;

double m_dIntercrossRate,

m_dAgamogenesisRate,

m_dMutantRate;

std::vector<Genetype> m_BestGeneme;

public:

void Initial(unsigned int iColonySize,

double dIntercrossRate,

double dAgamogenesisRate,

double dMutantRate);

void Release();

void NexGeneration();

void KeepColonySize(unsigned int size = 100)

private:

void Intercross();

void Agamogenesis();

void Mutant();

};

Population用std::vector容器保存物种的所有个体（m_iColonySize个Chromosome的实例），m_dIntercrossRate、m_dAgamogenesisRate和m_dMutantRate三个变量分别是交叉率、复制率和变异率，其中染色体交叉是自然界中生物繁殖的最常见方式，可以保证优秀的基因可以遗传到下一代或者有很大的机会使得部分优秀基因和另一部分优秀基因结合为一个非常优秀的染色体，因此交叉率比较高，一般取值在0.1～0.5之间；复制率即是无性繁殖的机率，无性繁殖在自然界中是普遍存在的正常现象（如植物中的落地生根和动物中的蚯蚓），无性繁殖可以确保优秀的个体有一定的机会壮大自己的种群，一般复制率取值在0.03～0.1之间；变异在自然界中是发生机率极小的事件，而且变异多是恶性的，所以变异率的取值范围在0.005～0.05之间，但变异可以让遗传算法跳出局部最优，因而是必须的一个操作算子。m_iColonySize是种群的大小，种群越大，找到解的机会越大，但花费的时间也相对比较多，一般设为可以接受的固定值，也可以编写与问题难度相关的函数来决定，本实验使用m_iColonySize=100的固定值方式。

Population另外还有一个关键函数NextGeneration()是实现种群进行一代繁殖操作的，它的实现如下：

void Population::NexGeneration(){

Intercross();

Agamogenesis();

Mutant();

}

很简单地调用了Intercross()、Agamogenesis()和Mutant()三个成员函数，下面以Intercross()的实现为例看看这三个函数是怎么实现繁殖操作的：

void Population::Intercross(){

unsigned int iIntercrossTimes = static_cast<unsigned int>(

m_Colony.size() * m_dIntercrossRate);

for(unsigned int i = 0; i < iIntercrossTimes; ++i){

unsigned int iChromoIdx1 = RangeRandom<unsigned int>(0, m_Colony.size());

unsigned int iChromoIdx2 = RangeRandom<unsigned int>(0, m_Colony.size());

if(iChromoIdx1 == iChromoIdx2){

++iChromoIdx2;

iChromoIdx2 = (iChromoIdx2 + 1) % m_Colony.size();

}

Chromosome* Chromo1 = new Chromosome;

Chromosome* Chromo2 = new Chromosome;

::Intercross(*m_Colony[iChromoIdx1],*m_Colony[iChromoIdx2],

*Chromo1, *Chromo2);

m_Colony.push_back(Chromo1);

m_Colony.push_back(Chromo2);

}

交叉操作先根据交叉率计算出要进行多少次交叉繁殖，然后在执行每一次交叉繁殖时随机选择两个染色体调用前文的Intercross算子实施交叉，并将新产生的两个新染色体加入到群体中。复制和变异都是相似的，因篇幅所限就不在这里赘述了，详见源码。

实验结果

遗传算法是有效但费时的一个算法。为了保证游戏运行流畅，我们不可能在每一次刷新的时候都执行一次遗传算法。因此隔多久执行一次遗传算法和控制遗传算法的遗传代数是很重要的。demo中是在控球权发生改变时执行遗传算法为red-blue两个球队计算新的站位方案的。同时为了游戏能比较流畅，遗传代数控制在20左右。

实验证明遗传算法对足球的决策有非常好的效果，主要表现为：1、使用遗传算法后，球员的站位比较到位，跑动积极。比较少进入Wait状态的结果就是当进攻或者防守的时候很容易在周边发现支持者可以轻易将球传出。这使得看起来球员之间的配合非常有默契，攻守两方都能打出更好的组合战术，增加了可观赏性。简单来说，就是加了遗传算法之后，踢的球越来越像人踢的。2、遗传算法加强了球队的对抗能力。未增加遗传算法的时候，运行本游戏20分钟总进球数在20~30，在增加遗传算法后，20分钟的总进球数减少到10~20个。主要原因是球员的站位更加合理，能根据当前的局势变换站位，这非常有效地抵抗了进攻，单刀入球也大大减少了。同时，在变换站位时球员的跑动积极，能够很好地增加的抢球和断球事件的发生，增强了两队的竞争。