BP神经网络的数学原理及其算法实现

转自http://blog.csdn.net/zhongkejingwang/article/details/44514073

BP网络的数学原理

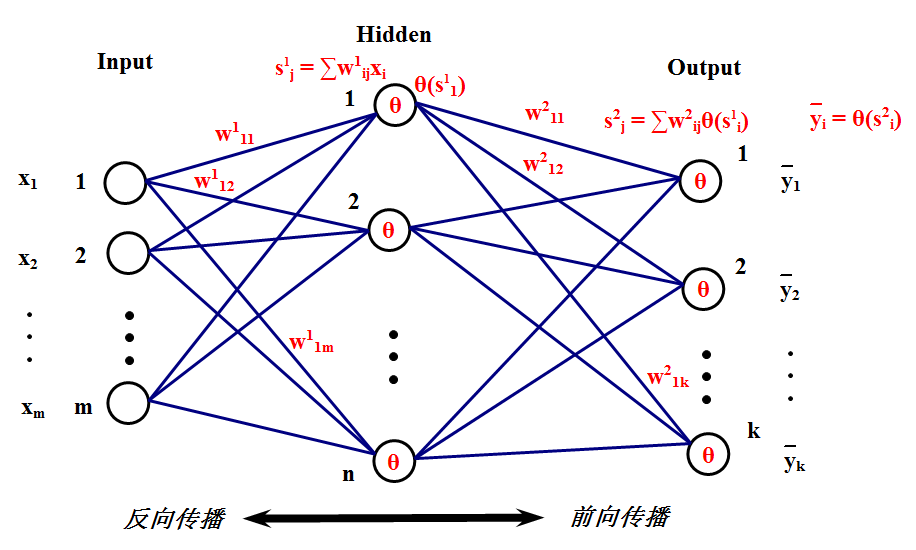
　　下面将介绍BP网络的数学原理，相比起SVD的算法推导，这个简直就是小菜一碟，不就是梯度吗求个导就完事了。首先来看看BP网络长什么样，这就是它的样子： 
　　
为了简单起见，这里只介绍只有一个隐层的BP网络，多个隐层的也是一样的原理。这个网络的工作原理应该很清楚了，首先，一组输入 x1、x2、…、xm 来到输入层，然后通过与隐层的连接权重产生一组数据 s1、s2、…、sn 作为隐层的输入，然后通过隐层节点的 θ(⋅) 激活函数后变为 θ(sj) 其中 sj 表示隐层的第 j 个节点产生的输出，这些输出将通过隐层与输出层的连接权重产生输出层的输入，这里输出层的处理过程和隐层是一样的，最后会在输出层产生输出 y¯j ，这里 j 是指输出层第 j 个节点的输出。这只是前向传播的过程，很简单吧？在这里，先解释一下隐层的含义，可以看到，隐层连接着输入和输出层，它到底是什么？它就是特征空间，隐层节点的个数就是特征空间的维数，或者说这组数据有多少个特征。而输入层到隐层的连接权重则将输入的原始数据投影到特征空间，比如 sj 就表示这组数据在特征空间中第 j 个特征方向的投影大小，或者说这组数据有多少份量的 j 特征。而隐层到输出层的连接权重表示这些特征是如何影响输出结果的，比如某一特征对某个输出影响比较大，那么连接它们的权重就会比较大。关于隐层的含义就解释这么多，至于多个隐层的，可以理解为特征的特征。 
　　前面提到激活函数 θ(⋅) ,一般使用S形函数（即sigmoid函数），比如可以使用log-sigmoid： θ(s)=11+e−s  
 
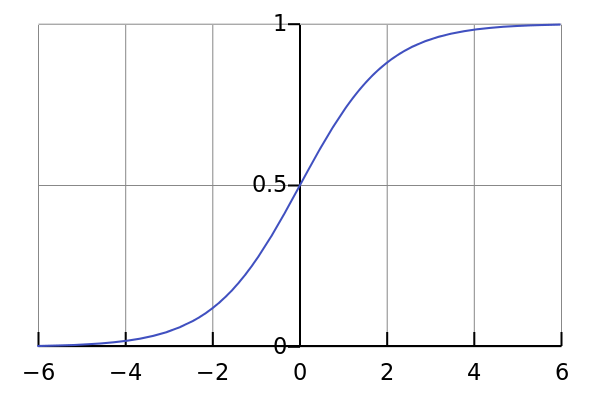
或者tan-sigmoid： θ(s)=es−e−ses+e−s  
 
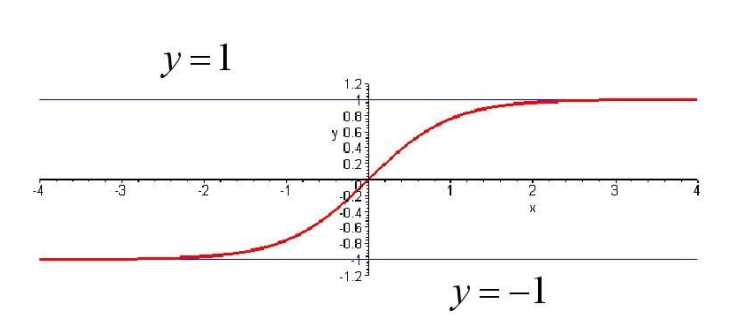
　　前面说了，既然在输出层产生输出了，那总得看下输出结果对不对吧或者距离预期的结果有多大出入吧？现在就来分析一下什么东西在影响输出。显然，输入的数据是已知的，变量只有那些个连接权重了，那这些连接权重如何影响输出呢？现在假设输入层第i个节点到隐层第j个节点的连接权重发生了一个很小的变化 Δwij ，那么这个 Δwij 将会对 sj 产生影响，导致 sj 也出现一个变化 Δsj ，然后产生 Δθ(sj) ，然后传到各个输出层，最后在所有输出层都产生一个误差 Δe 。所以说，权重的调整将会使得输出结果产生变化，那么如何使这些输出结果往正确方向变化呢？这就是接下来的任务：如何调整权重。对于给定的训练样本，其正确的结果已经知道，那么由输入经过网络的输出和正确的结果比较将会有一个误差，如果能把这个误差将到最小，那么就是输出结果靠近了正确结果，就可以说网络可以对样本进行正确分类了。怎样使得误差最小呢？首先，把误差表达式写出来，为了使函数连续可导，这里最小化均方根差，定义损失函数如下： 
　　

L(e)=12SSE=12∑j=0ke2j=12∑j=0k(y¯j−yj)2

　　用什么方法最小化 L ？跟SVD算法一样，用 随机梯度下降 。也就是对每个训练样本都使权重往其负梯度方向变化。现在的任务就是求 L 对连接权重 w 的梯度。 
　　用 w1ij 表示输入层第 i 个节点到隐层第 j 个节点的连接权重， w2ij 表示隐层第 i 个节点到输出层第 j 个节点的连接权重， s1j 表示隐层第 j 个节点的输入， s2j 表示输出层第 j 个几点的输入，区别在右上角标，1表示第一层连接权重，2表示第二层连接权重。那么有 
　　

∂L∂w1ij=∂L∂s1j⋅∂s1j∂w1ij

由于

s1j=∑i=1mxi⋅w1ij

所以

∂s1j∂w1ij=xi

代入前面式子可得 
　

∂L∂w1ij=xi⋅∂L∂s1j

接下来只需求出 ∂L∂s1j 即可。 
由于 s1j 对所有输出层都有影响，所以

∂L∂s1j=∑i=1k∂L∂s2i⋅∂s2i∂s1j

由于

s2i=∑j=0nθ(s1j)⋅w2ji

所以 
　　　

∂s2i∂s1j=∂s2i∂θ(s1j)⋅∂θ(s1j)∂s1j=w2ji⋅θ′(s1j)

代入前面的式子可得 
　　　

∂L∂s1j=∑i=1k∂L∂s2i⋅w2ji⋅θ′(s1j)=θ′(s1j)⋅∑i=1k∂L∂s2i⋅w2ji

现在记

δli=∂L∂sli

则隐层 δ 为

δ1j=θ′(s1j)⋅∑i=1kδ2i⋅w2ji

输出层 δ 为

δ2i=∂L∂s2i=∂∑kj=012(y¯j−yj)2∂s2i=(y¯i−yi)⋅∂y¯i∂s2i=ei⋅∂y¯i∂s2i=ei⋅θ′(s2i)

到这一步，可以看到是什么反向传播了吧？没错，就是误差 e ！ 
反向传播过程是这样的：输出层每个节点都会得到一个误差 e ，把 e 作为输出层反向输入，这时候就像是输出层当输入层一样把误差往回传播，先得到输出层 δ ，然后将输出层 δ 根据连接权重往隐层传输，即前面的式子： 

δ1j=θ′(s1j)⋅∑i=1kδ2i⋅w2ji

　现在再来看第一层权重的梯度： 
　

∂L∂w1ij=xi⋅δ1j

　第二层权重梯度： 
　

∂L∂w2ij=∂L∂s2j⋅∂s2j∂w2ij=δ2j⋅θ(s1i)

　可以看到一个规律： 每个权重的梯度都等于与其相连的前一层节点的输出（即 xi 和 θ(s1i) ）乘以与其相连的后一层的反向传播的输出（即 δ1j 和 δ2j ） 。如果看不明白原理的话记住这句话即可！ 
　这样反向传播得到所有的 δ 以后，就可以更新权重了。更直观的BP神经网络的工作过程总结如下： 
　
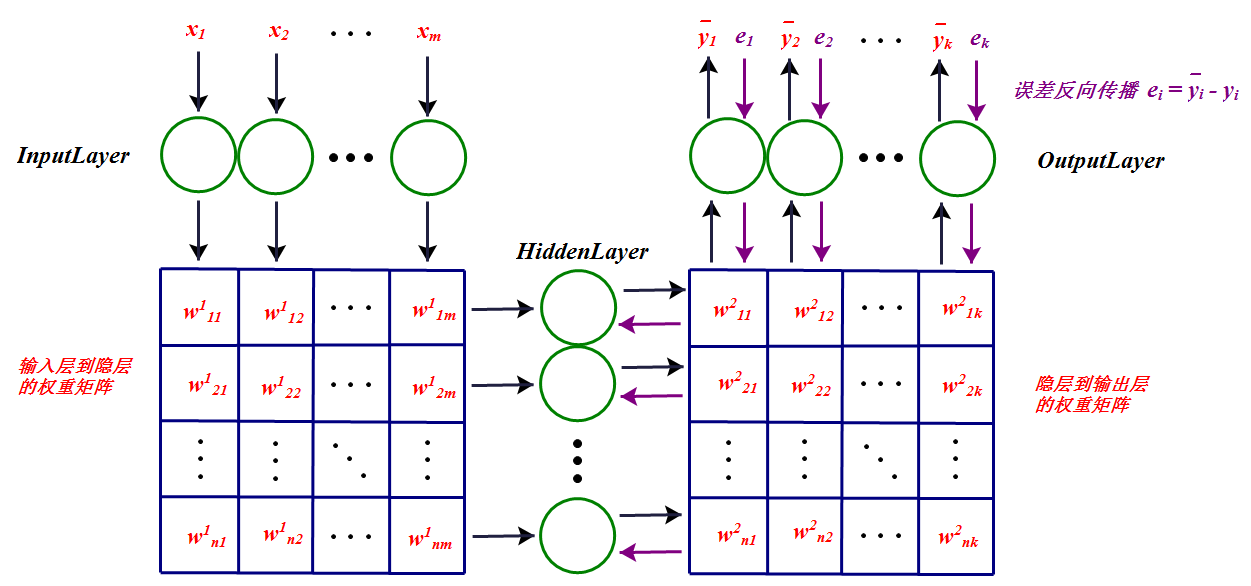
上图中每一个节点的输出都和权重矩阵中同一列（行）的元素相乘，然后同一行（列）累加作为下一层对应节点的输入。 
　为了代码实现的可读性，对节点进行抽象如下： 
　
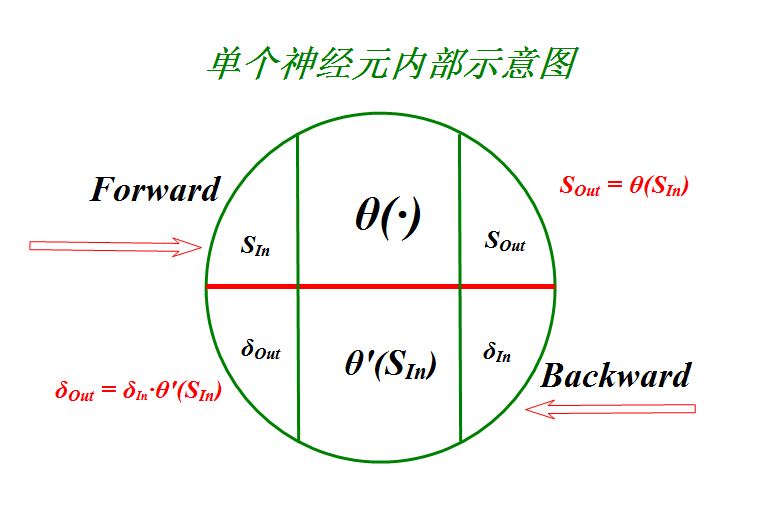
　这样的话，很多步骤都在节点内部进行了。 
　当 θ(s)=11+e−s 时， 
　

θ′(s)=θ(s)⋅(1−θ(s))=SOut⋅(1−SOut)

　当 θ(s)=es−e−ses+e−s 时， 
　

θ′(s)=1−θ(s)2=1−S2Out

BP网络原理部分就到这，接下来要根据上图中的神经元模型用代码实现BP网络，然后对Iris数据集进行分类。完整的代码见github： https://github.com/jingchenUSTC/ANN