我们先来看一张图
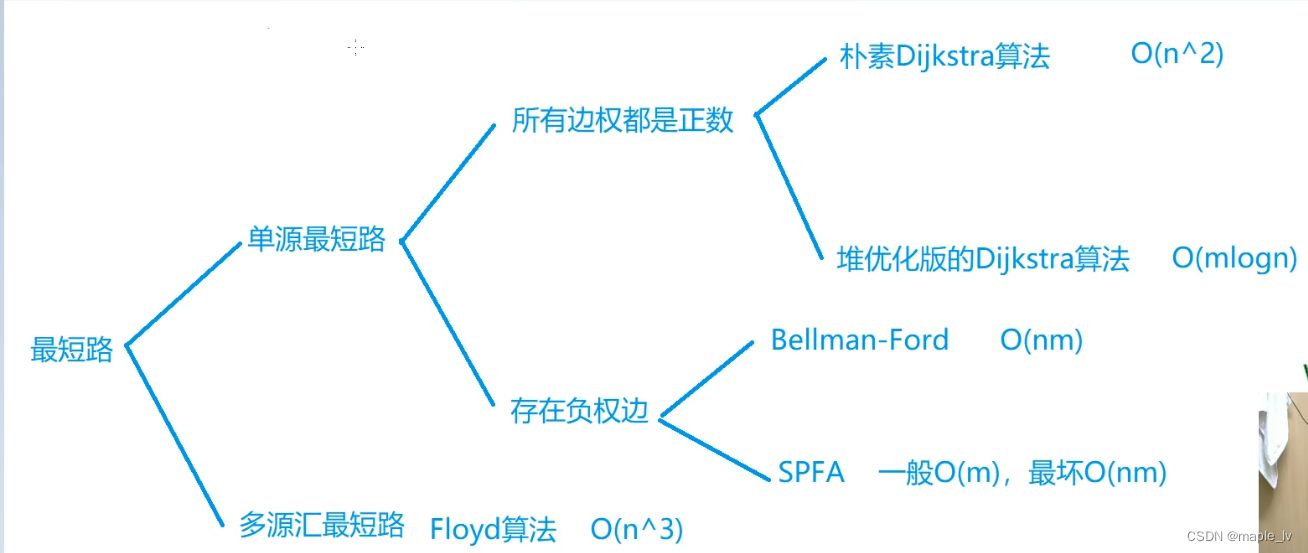
这张图就表示了在不同情况下,适用于不同情况下的最短路算法,我们先来看一下Dijkstra朴素算法
一样的我们先上一副图:

这幅图就大致展示了朴素Dijkstra算法的思路,这里再文字说明下:
集合S为已经确定最短路径的点集。
1. 初始化距离
一号结点的距离为零,其他结点的距离设为无穷大(看具体的题)。
2. 循环n次,每一次将集合S之外距离最短t的点加入到S中去(这里的距离最短指的是距离1号点最近。
点t的路径一定最短,基于贪心,严格证明待看)。然后用点t更新t邻接点的距离。
给定一个 n nn 个点 m mm 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 11 号点到 n nn 号点的最短距离,如果无法从 1 11 号点走到 n nn 号点,则输出 − 1 −1−1。
输入格式
第一行包含整数 n nn 和 m mm。
接下来 m mm 行每行包含三个整数 x , y , z x,y,zx,y,z,表示存在一条从点 x xx 到点 y yy 的有向边,边长为 z zz。
输出格式
输出一个整数,表示 1 11 号点到 n nn 号点的最短距离。
如果路径不存在,则输出 − 1 −1−1。
数据范围
1 ≤ n ≤ 500 , 1≤n≤500,1≤n≤500,
1 ≤ m ≤ 1 0 5 , 1≤m≤10^5,1≤m≤10
5
,
图中涉及边长均不超过 10000 1000010000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
1
2
3
4
输出样例:
3
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=510;
int g[N][N]; //为稠密阵所以用邻接矩阵存储
int dist[N]; //用于记录每一个点距离第一个点的距离
bool st[N]; //用于记录该点的最短距离是否已经确定
int n,m;
int Dijkstra()
{
memset(dist, 0x3f,sizeof dist); //初始化距离 0x3f代表无限大
dist[1]=0; //第一个点到自身的距离为0
for(int i=0;i<n;i++) //有n个点所以要进行n次 迭代
{
int t=-1; //t存储当前访问的点
for(int j=1;j<=n;j++) //这里的j代表的是从1号点开始
if(!st[j]&&(t==-1||dist[t]>dist[j]))//该步骤即寻找还未确定最短路的点中路径最短的点
t=j;
st[t]=true;
for(int j=1;j<=n;j++) //依次更新每个点所到相邻的点路径值
dist[j]=min(dist[j],dist[t]+g[t][j]);
}
if(dist[n]==0x3f3f3f3f) return -1; //如果第n个点路径为无穷大即不存在最低路径
return dist[n];
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof g); //初始化图 因为是求最短路径
//所以每个点初始为无限大
while(m--)
{
int x,y,z;
cin>>x>>y>>z;
g[x][y]=min(g[x][y],z); //如果发生重边的情况则保留最短的一条边
}
cout<<Dijkstra()<<endl;
return 0;
}
if(!st[j]&&(t==-1||dist[t]>dist[j]))

这里再解释下这句,如上图这种情况,假如2已经被标记过,再下一次循环我们的t应该是3还是4,很显然是4,为什么呢,因为从1到4的距离小于从1到3的距离。所以这一步我们是要确保到终点的最短路径。
堆优化dikstra算法
我们通过上面的算法可以发现,朴素的dijkstra算法是要遍历每一条边,找到最短的第一次遍历到的点t,然后对每一个点距离进行更新,其的时间复杂度为O(n^2),如果出现点众多的情况
例如10000个点,那么使用朴素的dijkstra算法必然会超时
所以人们针对了这种有众多点的情况用堆优化了dijkstra算法,使其的时间复杂度为O(mlogn)
这在解决有众多点而边数量偏少的稀疏图有奇效

看图:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
priority_queue<PII,vector<PII>,greater<PII>> q;
const int N = 150010;
int e[N],ne[N],w[N],h[N],idx;
int n,m;
int dist[N];
bool st[N];
void add(int a, int b, int c) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dijkstra() // 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
{
memset(dist, 0x3f, sizeof dist);
dist[1]=0;
q.push({0,1});
while (q.size()>0)
{
int point=q.top().second,distance=q.top().first;
q.pop();
if (st[point]==true)
{
continue;
}
st[point]=true;
for (int i=h[point];i!=-1;i=ne[i])
{
int t=e[i];
if (dist[t]>distance+w[i])
{
dist[t]=distance+w[i];
q.push({distance+w[i],t});
}
}
}
if (dist[n]==0x3f3f3f3f)
{
cout<<-1;
return;
}
else
{
cout<<dist[n]<<endl;
}
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
int a,b,c;
for (int i = 0; i < m; i ++ )
{
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
dijkstra();
return 0;
}有边数限制的最短路
题目:
给定一个n个点m条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从1号点到n号点的最多经过k条边的最短距离,如果无法从1号点走到n号点,输出impossible。
注意:图中可能 存在负权回路 。
输入格式
第一行包含三个整数n,m,k。
接下来m行,每行包含三个整数x,y,z,表示存在一条从点x到点y的有向边,边长为z。
输出格式
输出一个整数,表示从1号点到n号点的最多经过k条边的最短距离。
如果不存在满足条件的路径,则输出“impossible”。
数据范围
1≤n,k≤500,
1≤m≤10000,
任意边长的绝对值不超过10000。
1
2
3
输入样例:
3 3 1
1 2 1
2 3 1
1 3 3
输出样例:
3
1
2
3
4
5
6
7
什么是bellman - ford算法?
Bellman - ford算法是求含负权图的单源最短路径的一种算法,效率较低,代码难度较小。其原理为连续进行松弛,在每次松弛时把每条边都更新一下,若在n-1次松弛后还能更新,则说明图中有负环,因此无法得出结果,否则就完成。
(通俗的来讲就是:假设1号点到n号点是可达的,每一个点同时向指向的方向出发,更新相邻的点的最短距离,通过循环n-1次操作,若图中不存在负环,则1号点一定会到达n号点,若图中存在负环,则在n-1次松弛后一定还会更新)
算法思路看图:


#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510,M=1010;
int n,m,k;
int dist[N];
int backup[N];
struct edge
{
int a,b,w;
}edge[M];
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1]=0;
for (int i=0;i<k;i++)//循环几次就是题目限制几条边
{
memcpy(backup,dist,sizeof dist);//复制上一次的dist数组
for (int j=0;j<m;j++)
{
int a=edge[j].a,b=edge[j].b,w=edge[j].w;
dist[b]=min(dist[b],backup[a]+w);
}
}
if (dist[n]>0x3f3f3f3f/2)
{
return -1;
}
else
{
return dist[n];
}
}
int main()
{
scanf("%d%d%d", &n, &m,&k);
for (int i=0;i<m;i++)
{
int a,b,w;
scanf("%d%d%d", &a, &b,&w);
edge[i]={a,b,w};
}
int t=bellman_ford();
if (t==-1)
{
puts("imposible");
}
else
{
printf("%d\n",t);
}
return 0;
}Floyd算法:
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impossible。
数据保证图中不存在负权回路。
输入格式
第一行包含三个整数 n,m,k。
接下来 m 行,每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
接下来 k 行,每行包含两个整数 x,y,表示询问点 x 到点 y 的最短距离。
输出格式
共 k 行,每行输出一个整数,表示询问的结果,若询问两点间不存在路径,则输出 impossible。
数据范围
1≤n≤200,
1≤k≤n^2,
1≤m≤20000,
图中涉及边长绝对值均不超过 10000。
输入样例:
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3
输出样例:
impossible
1
floyd算法的原理是基于动态规划的基础上实现的,因为是稠密图我们通过邻接矩阵来存储,我们将各点距离初始化为正无穷(该点到自己的距离为0),然后进行三重循环,每层循环从第一个节点开始遍历,直至遍历到第n个节点,设最外层循环当前节点为k,中间层循环的当前节点为i,内层循环的当前节点为j。其中d[k, i, j]表示从i到j经过1到k个点的最短距离(k表示阶段),动态转移方程就是d[k, i, j] = min(d[k, i, j], d[k - 1, i, k] + d[k - 1, k, j]), 优化后变成 d[i, j] = min(d[i, j], d[i, k] + d[k, j])。我们以节点k为中介点,以节点i为起点,节点j为目标点,判断由起点i经由中介点k到达目标点j的代价值,是否小于由起点i直接到目标点j的代价值,若小于,则将从起点i到目标点j的代价值d[i][j]更新为d[i][k]+d[k][j]。

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 210, INF = 1e9;
int n, m, Q;
int d[N][N];
void floyd()
{
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main()
{
cin >> n >> m >> Q;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(i == j) d[i][j] = 0;
else d[i][j] = INF;
while(m--)
{
int a, b, c;
cin >> a >> b >> c;
d[a][b] = min(d[a][b], c);
}
floyd();
while(Q--)
{
int x, y;
cin >> x >> y;
if(d[x][y] > INF / 2) puts("impossible");//存在负权边
else cout << d[x][y] << endl;
}
return 0;
}





















 2949
2949











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








