《常微分方程》丁同仁+王高雄
一、一些前话
这学期课程较少,所以在提前学完微积分以后准备把之后的课程内容也提前学习了,我选用的教材是丁同仁先生的《常微分方程教程》和王高雄先生的《常微分方程》,预计是一个月读完(不过计划总是没有变化快,也没懒惰快······),所以重点是在于理解和掌握了,这也是我想写这一份每章总结的缘故(其实是学到一半发现啃不动了······)。水平过低,不免有错误,只是为了自学,有问题、建议的烦请指正
二、正题
第一章 基本概念
这一章主要讲的是一些基本的概念,如什么是微分方程、分为那两类、通解和特解的概念、初值问题、独立常数。也讲了微分方程和解的几何解释,线素(解在某点的切线),线素场(所有线素的集合)。
这里讲了一般构造线素场的方法就是建立一个斜率为k的等斜线。其实整个思想就是微积分的以直代曲的思想。
第二章 初等积分法
这一章是针对一些特殊的方程求解的方法,一般实际遇到的方程是是无法用这些方法解决的,不过呢这些基本的都不会怎么解别的方程呢?
- 恰当方程 将方程表达为另一个方程的微分,那这个方程=C就是通积分了,当然要判断是不是恰当方程只需要dx和dy前方程的偏导相等就行(dx前的对y,dy前的对x偏导)
- 变量分离,容易理解
- 一阶线性方程 分为齐次和非齐次 解法前者是变量的分离,而后者呢可以用因子法,也可以用常数变易法
- 初等变换法就是代换,比如齐次方程代y=kx,伯努利方程代z = y^(1-n)
- 一般化的积分因子法基本思想其实是同乘一个方程使其化为恰当方程,这部分需要偏微分方程的知识点,所以呢只有特殊情况下才能使用,比如积分因子只关于x或关于y。这一部分还有分组求积分因子等知识点
总结一下 都是一些基本的方法,没有什么理解的难度,题目灵活性另当别论
第三章 存在和唯一性定理
这一章的证明,尤其是皮卡序列的构造其实没有那么好理解(皮卡序列据说到复变的时候可以更好的理解这层思想)
首先定理的前提条件是初值问题中的f(x,y)是在给定区间内连续的,与此同时对y满足李氏条件(其实这可以等价为对y有连续的偏导)
这里重点说一下证明的思路,一共分五步:
- 首先原方程等价与定积分的形式,即y=y0 + ∫f(x,y)dx(从x0到x),这不难理解
- 构造皮卡序列,此序列必须满足y在给定区间内,这其实就是x范围中h的含义所在,有这个x限制于h的空间内,可以防止构造的序列超出所限定的范围,当然如果没有y范围的限定,我们就可以延拓他解的范围,这就是后文了
- 证明皮卡序列一致收敛到方程的解
- 皮卡序列极限就是其解,(极限和求和的互换),一致收敛的序列其极限函数收敛
- 证明唯一性,就是证明两解的差无限小
至此证明完毕,之后便是介绍了一个比李氏条件更弱的条件,Osgood条件,要确定一个关于r的函数F(r)代替李氏条件中的L,其实是包含李氏条件的
接下来就是佩亚诺存在定理
首先介绍了欧拉折线和Ascoli引理(等度连续和一致收敛的概念),然后先证明两个引理,其一是欧拉折线在h范围内至少有一个收敛的子序列,其二是欧拉折线在h范围内满足一个关系式,(很像皮卡序列,只是多出来一个趋于零的尾项)
最后就是佩亚诺了,f(x,y)连续,h范围内初值问题一定有一个解
接下来讲解的延拓,积分曲线会延伸到边界(要么无界),最大存在区间不会是闭集
*比较定理
第四章 奇解
1. 一阶隐式微分方程
主要就是微分法和参数法,这在王高雄里第二章就讲了,也是一个基本的方法
2.奇解
奇解呢就是有一个特殊的解,他上的每一点都有一个不同于他的解与他相切,求奇解的方法呢有p-判断法,就是通过原函数和原函数对p的导消p;还有c-判断法,这里提了一个包络的几何概念,也是消参数c;
两个判断法得到的函数不一定就是奇解,需要根据原函数和图像进行判断,当然还有直接的数学方法,可以参阅书籍对应章节及其证明
高阶微分方程
这其实就是我卡壳的地方,因为太求速度,而这一章用线性代数的语言给的记号太多所以到下一章时就有点遗忘,建议把这些记号的含义理解一下,总结一下,这当然就是我要干的了
自治(驻定)的微分方程,不明显包含自变量,可以降阶,但书中用的都是首次积分的方法,后面会了解,这里看看即可
还讲了二阶自治方程的几何作图法,了解一下,反正我看完就忘了。
构建一些系统对常微分方程有很多需求,第一节就演示了一两种,我专业不是数学,感觉自己数学学习其实问题很多,比如对数学知识的深层理解,因此我觉得自己可以看看《古今数学思想》或许可以更好的理解
1.n阶微分方程
 等价于n阶标准微分方程组
等价于n阶标准微分方程组
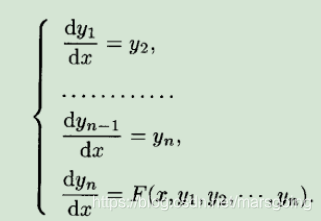 这样写呢未知数的个数就等于方程的阶数,更一般的方程的标准形式呢如下图,记为11
这样写呢未知数的个数就等于方程的阶数,更一般的方程的标准形式呢如下图,记为11
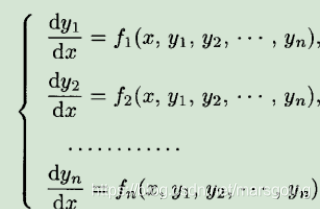
接下来就要用线性代数的语言来简洁化了(···)
n维的行向量

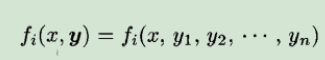


那么11就可以简化了,变成这个样子

然后引入模(范数),即可证明n维下的存在和唯一性定理、佩亚诺定理
然后谈到了线性微分方程组


但多把y写成列向量的形式
第六章 线性微分方程
存在和唯一性定理线性方程组满足初值条件的解在区间内史存在和唯一的
引理1任意两解(其实是n解)的线性组合也是方程的解
引理2线性空间s(所有解所组成的集合)是n维的(n代表阶数),证明使用一一对应的线性满映射通过同构得出
齐次微分方程有n个线性无关的解 S的基
Wronsky行列式

满足刘维尔公式

1.W不等于0,那线性方程组的解组是线性无关的(充要)
2.W恒等于0,那就是相关的(充要)
注意充要是针对线性方程组的解来说的,如果是一般的方程,第二条是不成立的(正向)
所以应用中我们只需计算某一点的W是否等于0,因为要么他恒等于0,要么恒不等于0
丁先生进一步引进记号,解组可以写为Y(x) = (yij(x))n×n,叫做方程组的解矩阵,且

若是基本解组,则叫基解矩阵,它乘以一个n维的常数列(任意)就是通解了。若这个常数列是非奇异的(满秩的),那么乘积也是个基解矩阵
非齐次线性方程组
其通解可以表示为特解加对应齐次的通解
另外还可以用常数变易法,只需要一个对应齐次的通解,就得到非齐次的通解

若再添加初值条件,则进一步的
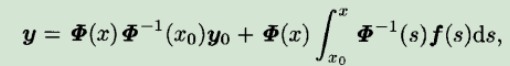
常系数线性微分方程组
所谓的常系数指A是n阶常数矩阵,设M是一个n阶矩阵组成的集合,那他的元素A的模定义为绝对值aij的和,由此可构建矩阵的指数函数:eA用级数展开

注意A0是指E,有这么几个性质:

exA是常数系线性微分方程的标准基解矩阵,标准指x=0时行列式等于1,或矩阵为E,由此非齐次的解是这样的:


为了能写成初等函数有限形式,作者用若尔当型来求基解矩阵,(思想是n阶矩阵A都存在非奇异的P使它化为若尔当标准型,每个若尔当块都可以拆成λE+幂零矩阵[ni次幂为零矩阵,然后利用三个性质化简和)证明详见书175页,这里上结论:第二种减少了求逆的过程,也是基解矩阵



但是求若尔当型和P都很麻烦,我们需要一些简单的替代方法
1.待定指数函数法
分两类(一)A只有单特征根,即没有重根,这时6.35的Ji可换为对应的λi,重点是求P,ri对应着P的列向量

(二)A有相重的根
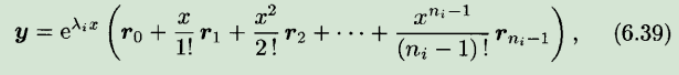
























 756
756

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








