warpAffine and Affine Transformation

Interface

from OpenCV: Geometric Image Transformations

◆ warpAffine()

void cv::warpAffine	(	InputArray	src,
		OutputArray	dst,
		InputArray	M,
		Size	dsize,
		int	flags = INTER_LINEAR,
		int	borderMode = BORDER_CONSTANT,
		const Scalar &	borderValue = Scalar()
	)

Python:
	cv.warpAffine(	src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]	) ->	dst

#include <opencv2/imgproc.hpp>

Applies an affine transformation to an image.

The function warpAffine transforms the source image using the specified matrix:

dst(x,y)=src(M11x+M12y+M13,M21x+M22y+M23)

when the flag WARP_INVERSE_MAP is set. Otherwise, the transformation is first inverted with invertAffineTransform and then put in the formula above instead of M. The function cannot operate in-place.

Parameters

src	input image.
dst	output image that has the size dsize and the same type as src .
M	2×3 transformation matrix.
dsize	size of the output image.
flags	combination of interpolation methods (see InterpolationFlags) and the optional flag WARP_INVERSE_MAP that means that M is the inverse transformation ( dst→src ).
borderMode	pixel extrapolation method (see BorderTypes); when borderMode=BORDER_TRANSPARENT, it means that the pixels in the destination image corresponding to the "outliers" in the source image are not modified by the function.
borderValue	value used in case of a constant border; by default, it is 0.

See also

warpPerspective, resize, remap, getRectSubPix, transform

Examples:

samples/cpp/image_alignment.cpp.

Tutorial

from OpenCV: Affine Transformations

Goal

In this tutorial you will learn how to:

• Use the OpenCV function cv::warpAffine to implement simple remapping routines.
• Use the OpenCV function cv::getRotationMatrix2D to obtain a 2×3 rotation matrix

Theory

What is an Affine Transformation?

1. ==>A geometric transformation that preserves lines and parallelism (but not necessarily distances and angles), every linear transformation is affine, but not every affine transformation is linear. (from wiki.)
2. ==>An affine transformation is any transformation that preserves collinearity (i.e., all points lying on a line initially still lie on a line after transformation) and ratios of distances (e.g., the midpoint of a line segment remains the midpoint after transformation). (from Affine Transformation -- from Wolfram MathWorld)
3. A transformation that can be expressed in the form of a matrix multiplication (linear transformation) followed by a vector addition (translation).

4. From the above, we can use an Affine Transformation to express:

   1. Rotations (linear transformation)
   2. Translations (vector addition)
   3. Scale operations (linear transformation)

   you can see that, in essence, an Affine Transformation represents a relation between two images.

5. The usual way to represent an Affine Transformation is by using a 2×3 matrix.

   

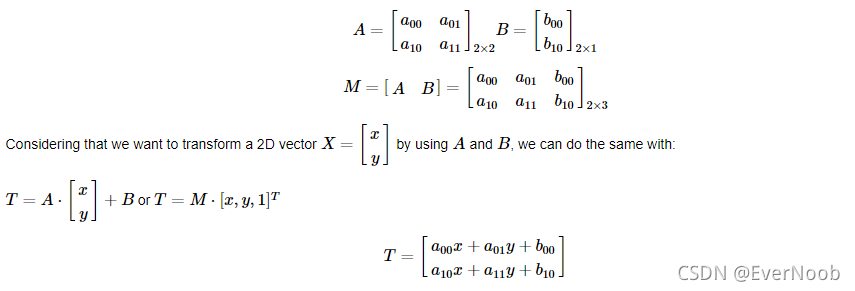
How do we get an Affine Transformation?

1. We mentioned that an Affine Transformation is basically a relation between two images. The information about this relation can come, roughly, in two ways:
   1. (a) We know both X and T and we also know that they are related. Then our task is to find M
   2. (b) We know M and X. To obtain T we only need to apply T=M⋅X. Our information for M may be explicit (i.e. have the 2-by-3 matrix) or it can come as a geometric relation between points.

2. Let's explain this in a better way (b). Since M relates 2 images, we can analyze the simplest case in which it relates three points in both images. Look at the figure below:

   

   the points 1, 2 and 3 (forming a triangle in image 1) are mapped into image 2, still forming a triangle, but now they have changed notoriously. If we find the Affine Transformation with these 3 points (you can choose them as you like), then we can apply this found relation to all the pixels in an image.

   1. ==> recall https://en.wikipedia.org/wiki/Rotation_matrix that 2d rotation matrices are 2*2 and the only true rotation variable is the angle theta.

   2. ==> 3 unknown, 3 equations: for affine transfomation matrices, we need to specify scaling factor alpha_ij, rotation angle theta and translational bias beta_ij, so a term like a_00 would be alpha_00 * cos(theta) 

      1. from Affine Transformation -- from Wolfram MathWorld

Code C++

• What does this program do?
  • Loads an image
  • Applies an Affine Transform to the image. This transform is obtained from the relation between three points. We use the function cv::warpAffine for that purpose.
  • Applies a Rotation to the image after being transformed. This rotation is with respect to the image center
  • Waits until the user exits the program

• The tutorial's code is shown below. You can also download it here

  #include "opencv2/imgcodecs.hpp"
  
  #include "opencv2/highgui.hpp"
  
  #include "opencv2/imgproc.hpp"
  
  #include <iostream>
  
  using namespace cv;
  
  using namespace std;
  
  int main( int argc, char** argv )
  
  {
  
  CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );
  
  Mat src = imread( samples::findFile( parser.get<String>( "@input" ) ) );
  
  if( src.empty() )
  
  {
  
  cout << "Could not open or find the image!\n" << endl;
  
  cout << "Usage: " << argv[0] << " <Input image>" << endl;
  
  return -1;
  
  }
  
  Point2f srcTri[3];
  
  srcTri[0] = Point2f( 0.f, 0.f );
  
  srcTri[1] = Point2f( src.cols - 1.f, 0.f );
  
  srcTri[2] = Point2f( 0.f, src.rows - 1.f );
  
  Point2f dstTri[3];
  
  dstTri[0] = Point2f( 0.f, src.rows*0.33f );
  
  dstTri[1] = Point2f( src.cols*0.85f, src.rows*0.25f );
  
  dstTri[2] = Point2f( src.cols*0.15f, src.rows*0.7f );
  
  Mat warp_mat = getAffineTransform( srcTri, dstTri );
  
  Mat warp_dst = Mat::zeros( src.rows, src.cols, src.type() );
  
  warpAffine( src, warp_dst, warp_mat, warp_dst.size() );
  
  Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );
  
  double angle = -50.0;
  
  double scale = 0.6;
  
  Mat rot_mat = getRotationMatrix2D( center, angle, scale );
  
  Mat warp_rotate_dst;
  
  warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );
  
  imshow( "Source image", src );
  
  imshow( "Warp", warp_dst );
  
  imshow( "Warp + Rotate", warp_rotate_dst );
  
  waitKey();
  
  return 0;
  
  }

Explanation C++

• Load an image:

CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );

Mat src = imread( samples::findFile( parser.get<String>( "@input" ) ) );

if( src.empty() )

{

cout << "Could not open or find the image!\n" << endl;

cout << "Usage: " << argv[0] << " <Input image>" << endl;

return -1;

}

• Affine Transform: As we explained in lines above, we need two sets of 3 points to derive the affine transform relation. Have a look:
  • for each point, the 3 affine matrices coefficients of transformation: scale, angle, bias can be mapped to 2 multipliers and constant offsets corresponding to the 2 dimensions of the image.

​Point2f srcTri[3];

srcTri[0] = Point2f( 0.f, 0.f );

srcTri[1] = Point2f( src.cols - 1.f, 0.f );

srcTri[2] = Point2f( 0.f, src.rows - 1.f );

Point2f dstTri[3];

dstTri[0] = Point2f( 0.f, src.rows*0.33f );

dstTri[1] = Point2f( src.cols*0.85f, src.rows*0.25f );

dstTri[2] = Point2f( src.cols*0.15f, src.rows*0.7f );

You may want to draw these points to get a better idea on how they change. Their locations are approximately the same as the ones depicted in the example figure (in the Theory section). You may note that the size and orientation of the triangle defined by the 3 points change.

• Armed with both sets of points, we calculate the Affine Transform by using OpenCV function cv::getAffineTransform :

​
Mat warp_mat = getAffineTransform( srcTri, dstTri );

We get a 2×3 matrix as an output (in this case warp_mat)

We then apply the Affine Transform just found to the src image
Mat warp_dst = Mat::zeros( src.rows, src.cols, src.type() );

warpAffine( src, warp_dst, warp_mat, warp_dst.size() );

with the following arguments:

• src: Input image
• warp_dst: Output image
• warp_mat: Affine transform ==> apparently can be take sets of points for geometric relations 
• warp_dst.size(): The desired size of the output image

We just got our first transformed image! We will display it in one bit. Before that, we also want to rotate it... ==> a single affine transformation should be sufficient, but a secondary constant rotation can sometimes conceptually or procedurally simplify the programmes.

• Rotate: To rotate an image, we need to know two things:

  1. The center with respect to which the image will rotate
  2. The angle to be rotated. In OpenCV a positive angle is counter-clockwise
  3. Optional: A scale factor

  We define these parameters with the following snippet:

Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );

double angle = -50.0;

double scale = 0.6;

• We generate the rotation matrix with the OpenCV function cv::getRotationMatrix2D , which returns a 2×3 matrix (in this case rot_mat)

Mat rot_mat = getRotationMatrix2D( center, angle, scale );

• We now apply the found rotation to the output of our previous Transformation:

Mat warp_rotate_dst;

warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );

• Finally, we display our results in two windows plus the original image for good measure:

imshow( "Source image", src );

imshow( "Warp", warp_dst );

imshow( "Warp + Rotate", warp_rotate_dst );

• We just have to wait until the user exits the program

waitKey();

Result

• After compiling the code above, we can give it the path of an image as argument. For instance, for a picture like:

  

  after applying the first Affine Transform we obtain:

  

  and finally, after applying a negative rotation (remember negative means clockwise) and a scale factor, we get: