维基百科计算方法:
举例:

解:
(1)最邻近插值法:
F(221.3, 396.7) = 45
(2)双线性插值法:
选择坐标系使得已知点坐标移动到(0,0)、(0,1)、(1,0)、(1,1)坐标点上
把 F(221, 396)=18当作坐标轴原点,则此时原来的点(221, 396)与转换后的点(0,0)的坐标映射关系为:x—>x-221,y—>y-396
F(221, 396)=18 —->F(0,0)=18
F(221, 397)=45 —->F(0,1)=45
F(222, 396)=52 —->F(1,0)=52
F(222, 397)=36 —->F(1,1)=36要计算的F(221.3,396.7)—>F(0.3, 0.7)
- 使用矩阵形式的计算形式
PS:使用维基百科介绍的插值公式形式本质是一样的
说明:坐标轴的转换仅改变元素的坐标(x, y),但不改变该元素的值F(x, y)












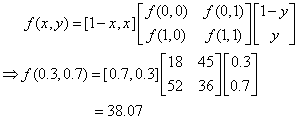
















 404
404

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








