赛题笔记《地铁乘客流量预测比赛》_城市交通系统客流量预测算法赛-CSDN博客

本文链接：https://blog.csdn.net/mintminty/article/details/107086077

第一部分

全球城市计算AI挑战赛总决赛
这个部分是自己在看决赛视频时，觉得印象深刻值得学习借鉴的点。

答辩人2：（25min左右）

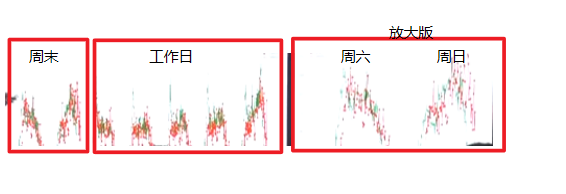
周末（图中前两簇）与工作日（图中后五簇）的流量差异，与站点类型有关 ，办公属性站点差异较大，旅游属性站点差异较小。所以纯粹以周末或非周末作为区分，可能不太合理
城际客流的“潮汐效应”，火车站站点的周六和周日流量会存在镜像分布的特点，就比如周六到火车站乘火车，周日乘火车返回再经过地铁回家。（注：周一和周五也存在类似特点）

答辩人5：（90min左右）

根据各站点在工作日早晚高峰的出站入站数，判断站点类型。如（1）工作日晚高峰入站形成波峰的站点被判定为工作地；（2）工作日早高峰入站形成波峰的站点被判定为居住地；（3）周末出入站人流远超于工作日人流的站点被判定为休闲娱乐地

答辩人1：

时间特征：星期/小时/分钟；是否周末；距离春节还有几天
流量特征（历史信息）：前两天同时段流量；前两天同时段前后两小时逐十分钟流量；历史所有星期 $x$ （要预测的星期 $x$ ）同时段逐小时流量均值；历史同时段逐十分钟流量均值
站点特征：站点id；站点闸机数；站点连接数；站点位置（类似POI 点，结果表示比较有效）

注：有一个未用的特征值得学习，作者可视化了入站出站的时间对应关系，比如7点入站的人对应出站时间的概率分布（结果显示比较集中）；12点入站的人对应出站时间的概率分布（结果显示比较分散）；18点入站的人对应出站时间的概率分布（结果显示比较集中）。

这个怎么用，作者说比如要预测今天早上7点的入站人次，将昨天晚上18点的出站特征加到现有的特征集中。

答辩人2：
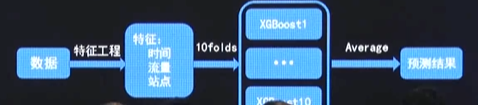
在这里插入图片描述

答辩人1：重特征工程，轻模型。
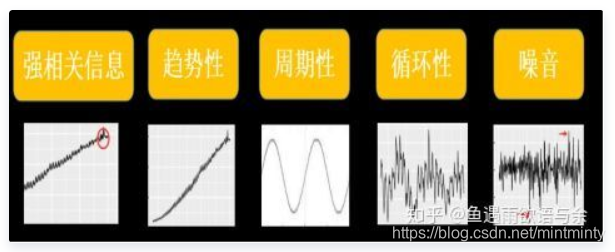
在这里插入图片描述

三种预测模式：

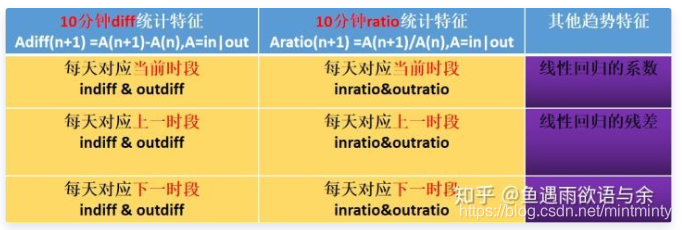
在这里插入图片描述

在这里插入图片描述

前后时段的差值 $A_{-} d i f f(n+1)=A(n+1)-A(n), A=i n \mid out$ 在这里既可以是出站流量，也可以是入站流量
前后时段的差比 $A_{-} \text {ratio}(n+1)=A(n+1) / A(n), A=\text {in } \mid \text { out }$