目录
Dijkstra算法简介
Dijkstra算法是一种贪心算法(详情见结尾),用于解决单源最短路径问题(详情见结尾)。给定一个加权有向图(详情见结尾),以及一个源节点,Dijkstra算法可以找到从源节点到图中所有其他节点的最短路径。
算法步骤
1. 初始化: 将源节点到所有其他节点的距离初始化为无穷大,将源节点到自身的距离初始化为0。
2. 选取最近节点: 从未处理的节点中选择距离源节点最近的节点。
3. 更新距离: 对于选取的最近节点,更新与其相邻节点的距离,若通过当前节点到达相邻节点的距离比已知的距离小,则更新距离。
4. 标记节点: 将选取的最近节点标记为已处理。
5. 重复步骤2-4,直至所有节点都被标记为已处理。
实例演示
让我们通过一个简单的示例来演示Dijkstra算法的工作原理。(图中的坐标只是位置的编号,两点之间的距离请见线段旁边标注的数字)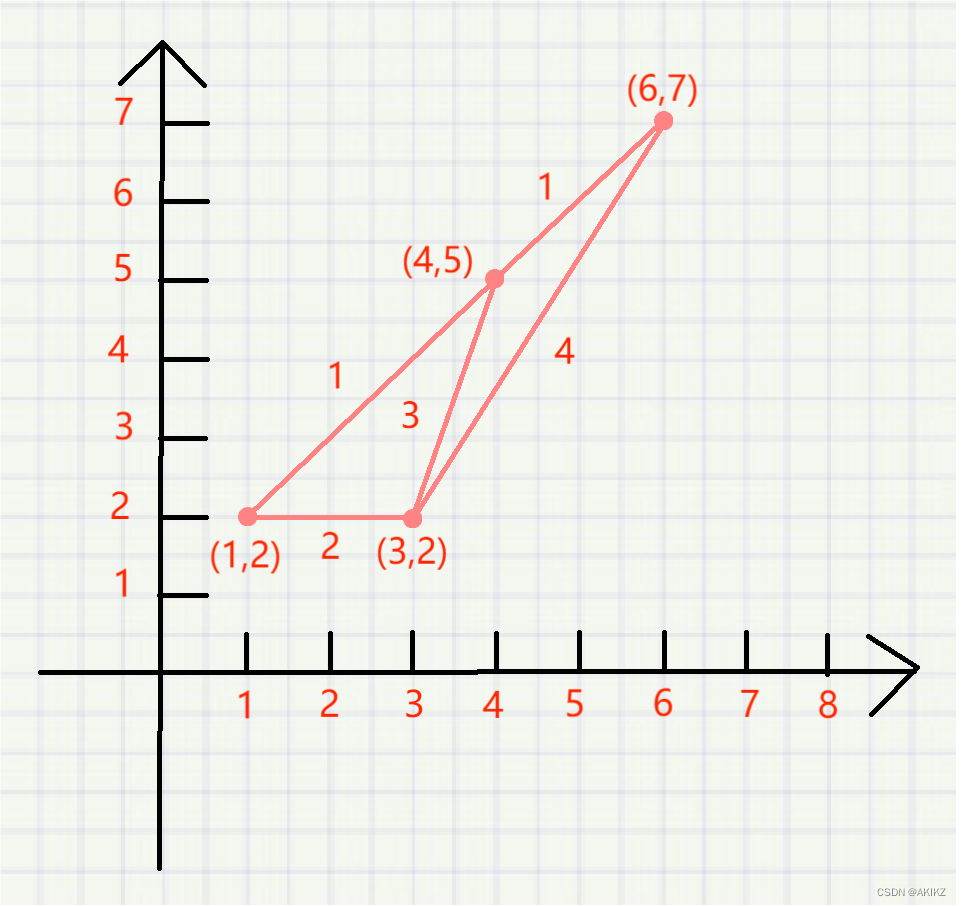
假设我们的源节点是(1,2),我们的目标是找到从(1,2)到(6,7)的最短路径。让我们用Dijkstra算法来解决这个问题。
步骤
-
初始化:选择一个起始顶点,这里我们选择
(1, 2)。将(1, 2)到自身的距离设为0,其他所有顶点的距离设为无穷大(可以用float('inf')表示)。 -
创建集合:创建一个集合
S,包含所有未确定最短路径的顶点。 -
开始算法:
- 从未确定最短路径的顶点中选择一个顶点(通常是距离最小的顶点)。
- 更新从源点到该顶点的所有邻接顶点的最短路径。
-
重复步骤3:将选定的顶点加入到集合
S中,并从集合中移除。然后重复步骤3,直到所有顶点都被加入到集合S中。 -
结束:当所有顶点都被考虑过时,算法结束。
Dijkstra算法流程
初始化:
- 距离
(1, 2)到自身为 0。- 距离
(3, 2)为无穷大。- 距离
(4, 5)为无穷大。- 距离
(6, 7)为无穷大。第一次迭代:选择
(1, 2),因为它是起始顶点,距离为0。
- 更新
(4, 5)的距离为(1, 2)到(4, 5)的权重1,即距离为1。- 更新
(3, 2)的距离为(1, 2)到(3, 2)的权重2,即距离为2。第二次迭代:选择距离最小的顶点
(4, 5),距离为1。
- 更新
(6, 7)的距离为(4, 5)到(6, 7)的权重1,即距离为2。第三次迭代:选择
(3, 2),距离为2。
- 由于
(3, 2)已经知道到(4, 5)的最短路径,不需要更新。- 更新
(6, 7)的距离为(3, 2)到(6, 7)的权重4,但这个路径比已知的路径长(2 + 4 > 2),所以不更新。后续迭代:所有其他顶点的距离都已经被确定,算法结束。
# pip install heapq import heapq def dijkstra(graph,start,end): graph[end] = {} # 初始化距离字典和已访问集合,infinity:无限 distances = {node:float('infinity') for node in graph} distances[start] = 0 queue = [(0,start)] visited = set() # 一个无序,不重复的元素集合 while queue: # 弹出距离最短的节点 # heapq.heappop:弹出并返回heap中的最小值,保持堆的不变性。 # current_node:节点 current_distance,current_node = heapq.heappop(queue) # 如果节点已经被访问过,则跳过 if current_node in visited: continue # 如果没有被访问,则放进visited visited.add(current_node) # 更新相邻节点的距离 # items() 方法以列表返回可遍历的(键, 值) 元组数组。[ (键,值) , (键,值) , (键,值) ] for neighbor,weight in graph[current_node].items(): distance = current_distance + weight if distance < distances[neighbor]: distances[neighbor] = distance heapq.heappush(queue,(distance,neighbor)) return distances[end] graph = { (1,2):{(4,5): 1,(3,2):2}, (3,2):{(4,5): 3,(6,7):4}, (4,5):{(6,7): 1}, # (6,7):{} # 假设这是终点,没有更多的邻居 } # 获取两个坐标之间的最短距离 start = (1,2) end = (6,7) distances = dijkstra(graph,start,end) print(distances)如果你想读入自己的数据,则需要以下代码(读入你自己的xls文件并转换为双层字典)
df = pd.read_excel(PATH) # 文件路径 data = df.set_index(df.columns[0]).T.to_dict('dict') # 双层字典 data = del_nan(data) # 如果数据里面有nan,如果没有则不需要调用此函数 def del_nan(d): if not isinstance(d, dict): return d # 如果不是字典,直接返回 return {k: del_nan(v) for k, v in d.items() if not (isinstance(v, float) and np.isnan(v))}结果
最终,我们得到了从
(1, 2)到所有其他顶点的最短路径长度:
(1, 2)到(1, 2):0(1, 2)到(3, 2):2(1, 2)到(4, 5):1(1, 2)到(6, 7):2注意,Dijkstra算法只能找到单个源点的最短路径。如果需要找到所有顶点对之间的最短路径,需要对图中的每个顶点都运行一次Dijkstra算法。
结论
Dijkstra算法以其简单、高效而闻名。通过不断地选择最近的节点并更新其相邻节点的距离,Dijkstra算法能够在有向图中找到源节点到所有其他节点的最短路径。这个算法的实现思路清晰,逻辑简单,但却在解决最短路径问题上展现出了强大的能力。
贪心算法
贪心算法是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最好或最优的算法策略。贪心算法不保证会得到最优解,但在某些问题中,贪心算法的解足够接近最优解或者确实是最优解。
贪心算法的特点
1. 贪心选择性质:在对问题求解的每一步,都采取在当前状态下最好或最优的选择。
2. 可行解:贪心算法做出的局部最优选择必须是可行解的组成部分,即,该选择必须不会导致不可行解。
3. 贪心选择条件:一个贪心选择是在当前状态下,与其他可选的任何选择相比,都被认为是最好的。
应用
贪心算法在解决一些最优化问题时非常有效,尤其是在那些具有“贪心选择”和“最优子结构”性质的问题中。例如:
- 钱币找零问题:使用最少数量的钱币来找零。
- 霍夫曼编码:数据压缩中的一种算法,通过构建最优的二叉树来实现。
- 图的最小生成树:在图论中,尝试找到一棵连接所有顶点的最小成本的树。
- 单源最短路径问题:如迪杰斯特拉算法(Dijkstra's algorithm)。
贪心算法的优点是简单、快速,但在很多问题中,贪心选择并不能保证得到全局最优解。在某些问题中,贪心算法可以证明其解是最优的,而在其他问题中,贪心算法可能只能得到近似解。
在实际应用中,是否使用贪心算法取决于问题的性质和对解的质量要求。如果问题是贪心选择和最优子结构性质的,贪心算法通常是一个好的选择。如果问题需要全局最优解,可能需要考虑其他算法,如动态规划。
单源最短路径问题
单源最短路径问题(Single-Source Shortest Path Problem)是图论中的一个经典问题,旨在找出从一个特定顶点(源点)到图中所有其他顶点的最短路径。这个问题在现实世界中有广泛的应用,比如路网导航、网络路由选择等。
解决方法
解决单源最短路径问题有多种算法,其中最著名的包括:
1. Dijkstra算法:适用于处理带有非负权重的图。它通过贪心策略逐步确定从源点到图中所有顶点的最短路径。
2. Bellman-Ford算法:可以处理带有负权重边的图,通过动态规划方法计算从单一源点到所有其他顶点的最短路径。
3. Floyd-Warshall算法:计算所有顶点对之间的最短路径,适用于密集图,并可以处理负权重边,但不适用于有负权重循环的图。
4. A*搜索算法:结合了Dijkstra算法和启发式搜索,通常用于图搜索中的路径规划问题,特别是在有明确目标的情况下。
Dijkstra算法的适用性
Dijkstra算法是解决单源最短路径问题的一种有效方法,但它有以下限制:
- 非负权重:算法假设图中所有的边的权重都是非负的。如果有负权重边,算法可能无法正确工作,因为它的贪心选择性质可能被违反。
- 贪心策略:算法在每一步都选择当前看起来最短的路径,这在有负面循环的情况下不总是能得到正确的结果。
Bellman-Ford算法的适用性
Bellman-Ford算法可以处理负权重边,但它的效率相对较低,特别是对于大型图。它通过反复松弛所有边来逐步改进路径长度的估计,直到达到最优解或检测到负面循环。
Floyd-Warshall算法的适用性
Floyd-Warshall算法适用于计算所有顶点对之间的最短路径,特别是当图中的顶点数量不是非常大时。它不是基于贪心策略,而是基于动态规划,计算每个顶点对的最短路径。
A*搜索算法的适用性
A*算法是Dijkstra算法的一个扩展,它使用启发式函数来引导搜索,通常用于有明确终点的路径规划问题,如游戏AI或地图导航。
选择算法
选择哪种算法取决于具体问题的性质,包括图的大小、边的权重是否为非负、是否需要找到所有顶点对之间的最短路径等。每种算法都有其特定的应用场景和优势。
加权有向图
加权有向图是一种图,其中的每条边都有一个与之关联的数值,称为权重或成本。这种图中的边具有方向,即从一个顶点指向另一个顶点,权重通常表示从一个顶点到另一个顶点的某种成本或距离。
加权有向图的特点
1. 方向性:边具有方向,这意味着从一个顶点到另一个顶点的路径可能与反向路径不同。
2. 权重:每条边都有一个与之关联的权重,可以是正数、负数或零。
3. 顶点:图中的节点,也称为顶点或结点,代表图中的实体。
4. 边:连接两个顶点的线段,表示实体之间的关系。
应用场景
加权有向图在许多实际问题中都有应用,例如:
- 路网分析:边的权重可以表示道路的距离或行驶时间。
- 网络路由:在互联网或通信网络中,边的权重可以代表数据传输的成本或延迟。
- 供应链管理:边的权重可以表示物料或产品在供应链各环节间的运输成本。
- 资源分配问题:权重可以表示不同资源分配方案的成本效益。
解决问题
在加权有向图中,常见的问题包括:
1. 最短路径问题:找出从一个顶点到另一个顶点的最短路径(即总权重最小的路径)。
2. 最大流问题:在网络流中,确定从一个源点到一个汇点的最大可能流量。
3. 最小生成树问题:在加权图中找到一棵连接所有顶点的树,使得边的总权重最小。
算法
针对加权有向图中的最短路径问题,可以采用以下算法:
1. Dijkstra算法:适用于边的权重为非负的情况。
2. Bellman-Ford算法:可以处理边的权重为负数的情况,但需要更多的计算资源。
3. A*搜索算法:结合了Dijkstra算法和启发式搜索,适用于有明确终点的路径规划问题。
实例演示
假设有一个加权有向图,其中包含5个节点(标记为A, B, C, D, E),以及它们之间的带权有向边。这个图可以用邻接矩阵或邻接列表来表示。这里,提供一个邻接列表(详情见结尾)的示例:
# pip install networkx # pip install matplotlib import networkx as nx import matplotlib.pyplot as plt # graph 是一个字典,其键是图中的节点,值是一个字典 # 表示从该节点出发可以到达的其他节点及其对应的权重。 # 例如,'A': {'B': 3, 'C': 1} 表示从节点A可以到达节点B,权重为3,也可以到达节点C,权重为1。 graph = { 'A': {'B': 3, 'C': 1}, 'B': {'A': 2, 'D': 4, 'E': 5}, 'C': {'D': 2}, 'D': {'C': 1, 'E': 3}, 'E': {'A': 1} } # 创建有向图 G = nx.DiGraph() # 添加节点 G.add_nodes_from(['A', 'B', 'C', 'D', 'E']) # 添加带权边 G.add_weighted_edges_from([('A', 'B', 3), ('A', 'C', 1), ('B', 'A', 2), ('B', 'D', 4), ('B', 'E', 5), ('C', 'D', 2), ('D', 'C', 1), ('D', 'E', 3), ('E', 'A', 1)]) # 绘制图形 nx.draw(G, with_labels=True, font_weight='bold') edge_labels = nx.get_edge_attributes(G, 'weight') pos = nx.spring_layout(G) nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels) # 显示图形 plt.show()在这个图中,每个箭头上方的数字表示从起点到终点的权重。如果我们想找出从A到F的最短路径,我们可以使用Dijkstra算法或Bellman-Ford算法来解决。
注意事项
- 在使用Dijkstra算法时,必须确保所有边的权重都是非负的,因为算法的贪心选择性质依赖于这一条件。
- 如果图中存在负权重边,应使用Bellman-Ford算法或其它能够处理负权重的算法。
- 在实际应用中,根据问题的具体情况和图的特性选择合适的算法是非常重要的。
邻接列表
邻接列表(Adjacency List)是图数据结构中的一种表示方法,用于存储图中顶点的邻接信息。在邻接列表表示中,每个顶点都与一个列表相关联,列表中的元素表示该顶点可以到达的其他顶点(即邻接顶点)以及相应的边的信息(如权重)。这种表示方法在稀疏图(边的数量远小于顶点对数量)中特别有效,因为它可以节省存储空间。
邻接列表的特点
1. 空间效率:由于稀疏图中边的数量远小于可能的边数,邻接列表通常比邻接矩阵(Adjacency Matrix)占用更少的存储空间。
2. 动态存储:邻接列表可以根据需要动态地添加或删除边,而不需要重新分配整个矩阵的存储空间。
3. 灵活性:邻接列表可以很容易地表示有向图和无向图,以及加权或无权图。
邻接列表的表示
邻接列表通常使用数组或列表(在某些编程语言中)来实现。每个顶点索引对应数组中的一个位置,该位置存储了一个列表,包含了该顶点的所有邻接顶点以及边的信息。
例如,考虑以下无向加权图:
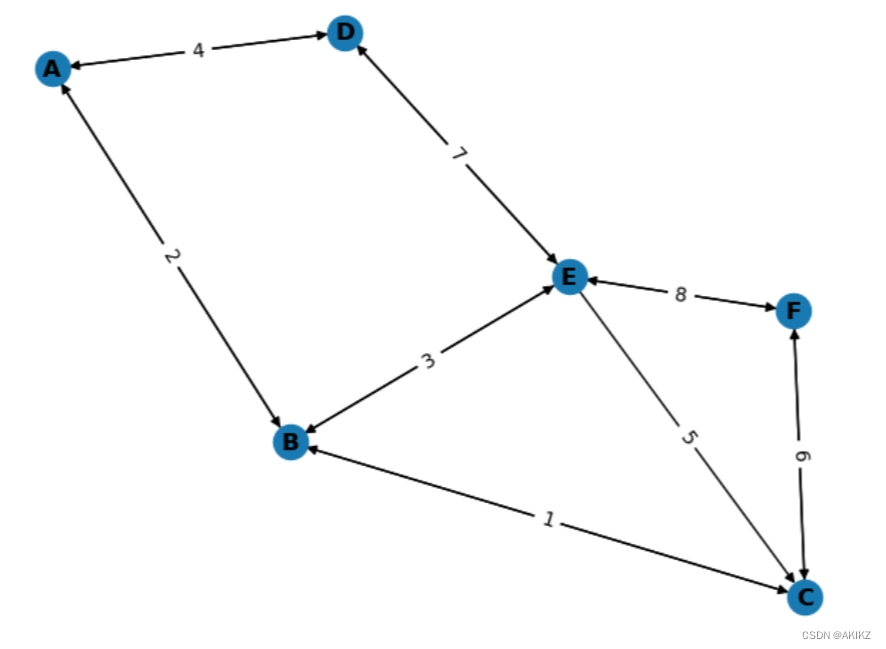
该图的邻接列表表示可以是:
graph = {
'A': [('B', 2), ('D', 4)],
'B': [('A', 2), ('C', 1), ('E', 3)],
'C': [('B', 1), ('F', 6)],
'D': [('A', 4), ('E', 7)],
'E': [('B', 3), ('D', 7), ('C', 5), ('F', 8)],
'F': [('C', 6), ('E', 8)]
}在这个表示中,每个顶点(键)都有一个与之关联的元组列表,元组中的第一个元素是邻接顶点,第二个元素是边的权重。
使用邻接列表的算法
邻接列表常用于实现图的遍历和搜索算法,如:
1. 深度优先搜索(DFS):从图中的任意顶点开始,沿着邻接列表递归遍历所有可达顶点。
2. 广度优先搜索(BFS):使用队列从源顶点开始,逐层遍历所有可达顶点。
3. Dijkstra算法:用于在加权图中找到从单个源点到所有其他顶点的最短路径。
4. Prim或Kruskal算法:用于在加权图中找到最小生成树。
注意事项
- 在使用邻接列表时,需要注意顶点的索引或键的一致性,以确保正确地访问和更新邻接信息。
- 对于密集图(边的数量接近顶点对数量),邻接矩阵可能是更有效的表示方法,因为它允许快速地检查两个顶点之间是否存在边。






















 5118
5118

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








