#数组 #Java #长度最小的子串
Feeling and experiences:
有序数组的平方:力扣题目链接
该题读一遍题目以后,发现这题这么简单?
直接入手,写完就解答错误了......题目中存在一些细节,比如非递减序列,想了想不就是升序吗?但是题目想提示你的其实就是这个数组中存在负数的情况。
一个负数越小,意味着它的平方也就越大,对应着在结果数组的位置就越靠后(因为要求升序排列)
注意到这个点之后,我第一个想到的方法就是先循环遍历,把数组中每个数的平方算出来,再给它们进行排序。写出来的代码看起来很简单,但时间复杂度上却是O(n*logn,基与快速排序)。
那么要优化它的时间效率,我考虑到了双指针的方法,以下是我的解题思路与代码:
class Solution {
public int[] sortedSquares(int[] nums) {
//利用双指针的解法
//为什么会想到用双指针?因为本题的关键一点在于数组中存在负数,那么负数的平方可能会很大
//也就是说,在这个非递减排序中,越靠前的负数也就越小,它的平方也就越大
//创建一个数组来记录结果
int []res = new int[nums.length];
//设置一个末尾指针
int end = nums.length-1;
//进入for循环
for(int i =0,j=nums.length-1;i<=j;){
//i,j就分别代表要处理的数,这里先不进行i++与j--操作
if(nums[i]*nums[i]>=nums[j]*nums[j]){
//也就是说当前这个数的平方比尾指针指向的数的平方要大,那我们就把该数平方放到res数组中(end指向的位置)
res[end--] = nums[i]*nums[i];
//这个时候才让i++ (因为i这个位置的数已经处理过了)
i++;
}
else{
//也就是nums[i]的平方比nums[end]小
//本来这个数的平方都更小,那说明它的原数也更小,所以我们把end这个位置指向的数的平方添加到res数组中
res[end--] = nums[j]*nums[j];
//这个时候让j--
j--;
}
}
return res;
}
}长度最小的子数组:力扣题目链接
最开始直接入手暴力解法:

但是写完后测试,发现了里面的错误,噢~原来题目要求的是大于等于target(而且我在同一次迭代中两次将nums[j]添加到了sum),先把这次的错误记录下来。(大家也可看看这个存在的逻辑错误)
迅速看卡哥的暴力解法,发现了里面的妙处(虽然是暴力解法,但是也有很多值得思考的地方)
以下是正确的暴力解法思路与代码:
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int minlen = Integer.MAX_VALUE; //记录最小的子数组长度
int sum; //用来记录各数之和
for(int i =0;i<nums.length;i++){
sum = 0;
for(int j =i;j<nums.length;j++){
sum += nums[j];
if(sum>=target){
sum+=nums[j];
//如果和已经大于等于target了,则更新minlen的值
minlen = Math.min(minlen,j-i+1);
break; //更新完就退出内循环
}
}
}
return (minlen == Integer.MAX_VALUE)?0:minlen;
}
}
但是提交测试后就发现,已经超过时间限制了。(时间复杂度为O(n^2))
所以我们还得换一种方法
在卡哥的讲解视频中,运用到了滑动窗口的思路。
我在初次接触到滑动窗口时,最开始没有解读到精髓,一下就认为这和暴力循环不是一样的思路吗?sum>=target了,初始位置就后移一个。
后来我琢磨出来,它和暴力循环的思路,像但又不像,它的本质确实也是当sum>=target了,初始位置后移,但是最有意思的就是初始位置的移动不依赖另外一个指针的移动,也就是说,它们是相互配合的关系,而不是像双层for循环一样,我外循环指针要移动必须要等内循环执行完,这样效率就太慢了。
这里放一张代码随想录的图,一眼就能直观的看出:

精髓就在于这个while循环! (注意:不要以为for里放一个while就以为是O(n^2)啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)。)
以下是我的理解与代码:
class Solution {
public int minSubArrayLen(int target, int[] nums) {
//利用滑动窗口
//首先要提的就是滑动窗口的精髓在于起始位置的移动
int res = Integer.MAX_VALUE; //同理,还是先用一个最大值便于后续的更新
int sum =0;
int i =0;
for(int j =0;j<nums.length;j++){
sum+=nums[j];
while(sum>=target){
//如果target大于等于目标值了,此时我们就要更新res
res = Math.min(res,j-i+1);
//然后初始位置向后移动,更新初始位置与sum
sum -= nums[i++]; //sum = sum - 当前初始位置的值,初始位置再后移动一个
//这样就做到了如果我的sum只要大于等于目标值,我就一直在while循环中更新我的初始位置,出了while循环又可以更新末尾位置,这样效率就提高了
}
}
return (res == Integer.MAX_VALUE)?0:res;
}
}螺旋矩阵II:力扣题目链接
这是一道模拟题,不涉及到具体的算法。
直接上代码:
class Solution {
public int[][] generateMatrix(int n) {
int loop = 0; // 控制循环次数
int[][] res = new int[n][n];
int start = 0; // 每次循环的开始点(start, start)
int count = 1; // 定义填充数字
int i, j;
while (loop++ < n / 2) { // 判断边界后,loop从1开始
// 模拟上侧从左到右
for (j = start; j < n - loop; j++) {
res[start][j] = count++;
}
// 模拟右侧从上到下
for (i = start; i < n - loop; i++) {
res[i][j] = count++;
}
// 模拟下侧从右到左
for (; j >= loop; j--) {
res[i][j] = count++;
}
// 模拟左侧从下到上
for (; i >= loop; i--) {
res[i][j] = count++;
}
start++;
}
if (n % 2 == 1) {
res[start][start] = count;
}
return res;
}
}
熟悉这个模拟的过程,忘了就看看卡哥的讲解视频和图解——视频链接
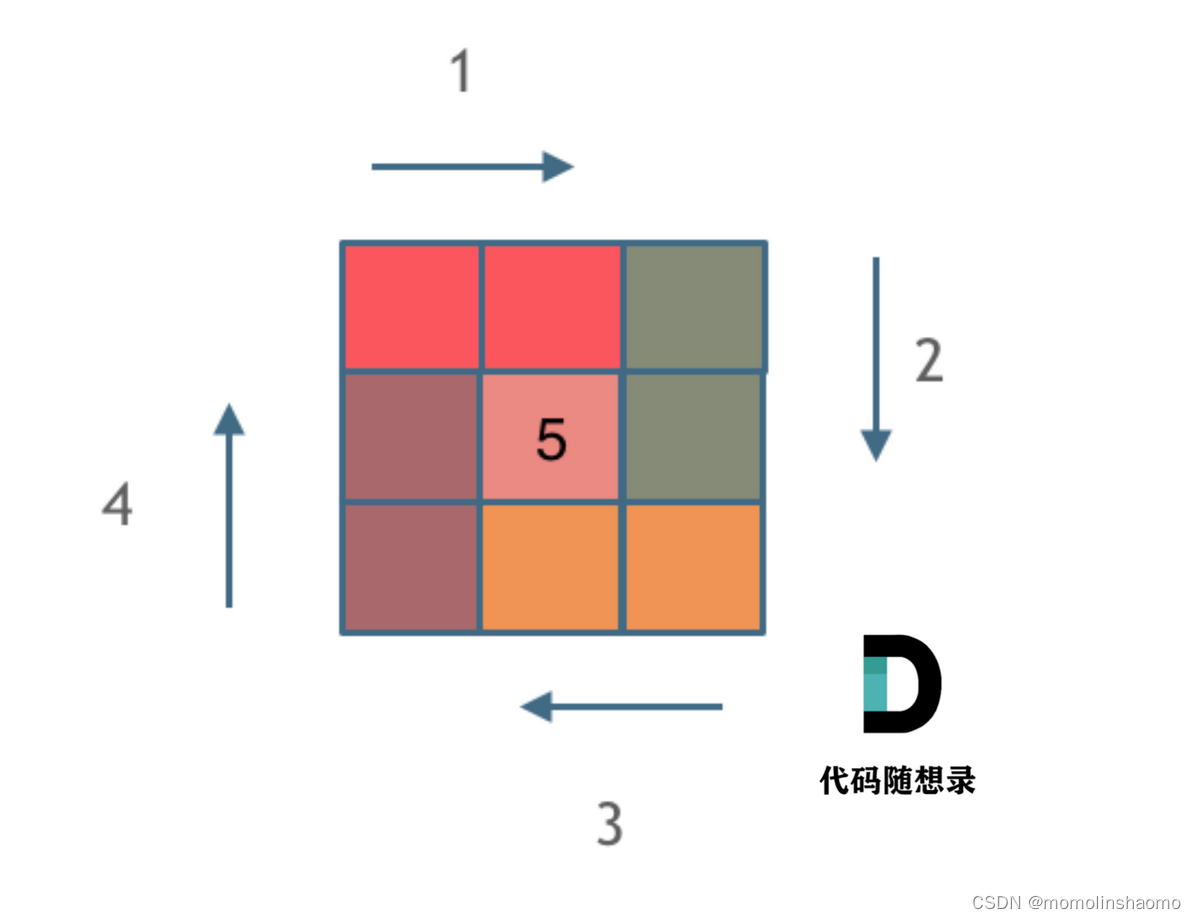
模拟顺时针画矩阵的过程:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
回顾一下二分涉及到的循环不变量!
“少年向来不识天高地厚,放眼处,皆是才高八斗
虽是自命风流,倒也坦诚无忧
谦和又狂妄,骄傲又坦然!”
Fighting!
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








