GESP 2025年3月C++ 3级 真题与解析

答案：D

解析：输入10字节，其中9字节扩展为12字节，剩下1字节补充为4字节，一共16字节。

答案：B

解析：如下：

A. 0xC0 0x80

• 0xC0 → 11000000（符合 2 字节首字节）
• 0x80 → 10000000（合法后续字节）
  问题：
  • 此组合解码为 Unicode U+0000（NULL 字符），但 UTF-8 要求 U+0000 必须用单字节 0x00 表示（最短编码原则）。
  • 结论：非法（冗余编码）。

B. 0xF0 0x90 0x80 0x80

• 0xF0 → 11110000（符合 4 字节首字节）
• 0x90 → 10010000（合法后续字节）
• 0x80 → 10000000（合法后续字节）
• 0x80 → 10000000（合法后续字节）
  解码：
  • 有效 Unicode 码点 U+10000（补充平面字符）。
  • 结论：合法。

C. 0x80 0x80 0x80

• 0x80 → 10000000（不能作为首字节！）
  • UTF-8 要求首字节非 10...。
  • 结论：非法。

D. 0xFF 0xFE 0xFD

• 0xFF → 11111111（无对应的 UTF-8 编码模式）
  • 首字节不能为全 1。
• 0xFE → 11111110（同样非法）
• 0xFD → 11111101（非法）
  • 结论：非法（无效首字节）。

答案：A

解析：如下：

1. 整数部分（111）的二进制转换

使用 除2取余法，直到商为0：

除法步骤	商	余数
111 ÷ 2	55	1
55 ÷ 2	27	1
27 ÷ 2	13	1
13 ÷ 2	6	1
6 ÷ 2	3	0
3 ÷ 2	1	1
1 ÷ 2	0	1

从下往上读取余数，得到：
111 (十进制) = 1101111 (二进制)

---

2. 小数部分（0.111）的二进制转换

使用 乘2取整法，直到小数部分为0或达到所需精度：

乘法步骤	积	整数部分
0.111 × 2	0.222	0
0.222 × 2	0.444	0
0.444 × 2	0.888	0
0.888 × 2	1.776	1
0.776 × 2	1.552	1
0.552 × 2	1.104	1
0.104 × 2	0.208	0
0.208 × 2	0.416	0
0.416 × 2	0.832	0
0.832 × 2	1.664	1

从上往下读取整数部分，得到：
0.111 (十进制) ≈ 0.0001110010 (二进制)（保留10位）

---

3. 合并整数和小数部分

• 整数部分：1101111
• 小数部分：0001110010

最终结果：
111.111 (十进制) ≈ 1101111.0001110010 (二进制)

答案：B

解析：补码简化了加减法运算，减法只需要按照加法运算即可，因此计算机只需要加法器，不需要减法器，简化电路。

答案：A

解析：

1. 具体范围计算

• 非负数范围（符号位 0）：
  • 最小值：00000000（0）。
  • 最大值：01111111（127，即 27−127−1）。
• 负数范围（符号位 1）：
  • 最小值：10000000（-128，通过补码规则直接表示）。
  • 最大值：11111111（-1）。

2. 关键点解释

• 为什么最小负数是 -128？
  在补码中，10000000 被特殊定义为 -128（而非 -0），因为：
  • 按补码公式：−27=−128−27=−128。
  • 这是8位补码能表示的最小值，没有对应的正数 +128。
• -1 的表示：
  11111111（所有位为 1），因为：

−1=−27+(26+25+⋯+20)=−128+127=−1.−1=−27+(26+25+⋯+20)=−128+127=−1.

答案：C

解析：32位系统（unsigned int 占32位）：

• a=−5的补码表示：11111111 11111111 11111111 11111011。
• 转换为无符号整数时，直接解释为二进制对应的正数：

b=232−5=4294967296−5=4294967291

Tips：排除A和D，负数第一位为1，变成无符号以后不可能还是5，所以排除B，最后选C。

答案：A

解析：一眼

第 9 题 下⾯程序是将⼗进制转⼗六进制，横线处应该填⼊的是（）

答案：C

解析：一眼

答案：D

解析：一眼

答案：D

解析：i从1开始，maxIndex从0开始，如果arr[i]>arr[maxIndex]就记录i

答案：D

解析：第8行判断了奇数，第9行肯定就要判断偶数，所以从A、B、D里选，第8行left++，说明奇数从左往右放，而right初试值为4，是最大的索引值，所以肯定是right--，A里判断arr[left]不对，left是给奇数用的，B里lef- -也不对，所以是D。

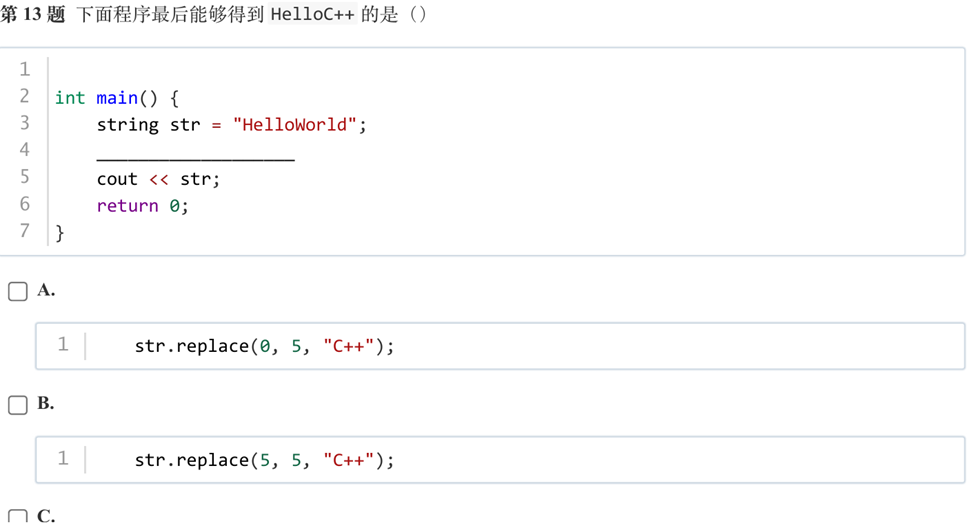
答案：B

解析：从W开始替换，替换5个。这题没有出替换3个的选项，如果只替换3个，还会保留ld，更有迷惑性。

答案：D

解析：insert是插在第i个后面，i从1开始。Substr是从i个开始取，i从0开始。

A,    插第4个后面，然后取4到8，输出：worl

B,    输出C++

C,    insert的第一个参数必须是整型

B,    输出World

答案：C

解析：一眼

答案：F

解析：判断方法还有很多，至少还有任意两边长度之差小于第三边。

答案：T

解析：按位与，如果最后一位是1，说明是奇数。

答案：T

解析：一眼

答案：T

解析：是被3和5同时整除，3和5互质，就是被15整除

答案：T

解析：每个同学有 2 种选择（参加或不参加），且所有同学的选择是独立的。
根据 乘法原理，总的选择方式为：

2×2×⋯×2=2n2×2×⋯×2=2n

答案：T

解析：（2025）10=（0111 1110 1001）2

答案：T

解析：一眼

答案：T

解析：（A+B）10=(21)10=(18)13

答案：T

解析：一眼

答案：T

解析：如下

第一步：十九进制 → 十进制

十九进制数字解析

• 十九进制使用数字 0-9 和字母 A-I（其中 A=10, B=11, ..., I=18）。
• CCF 的各位：
  • C = 12
  • C = 12
  • F = 15（注意：在十九进制中，F 是合法的，但通常十九进制字母只到 I（18）。这里假设 F=15。）

转换为十进制

按权展开：

CCF19=C×192+C×191+F×190CCF19​=C×192+C×191+F×190

代入数值：

=12×361+12×19+15×1=12×361+12×19+15×1

计算：

=4332+228+15=457510=4332+228+15=457510​

验证：
如果 F 在十九进制中无效（超出 I），需确认题目是否有误。假设题目正确，继续。

---

第二步：十进制 → 十三进制

将十进制数 4575 转换为十三进制。

短除法（除13取余法）

1. 计算步骤：
   • 4575 ÷ 13 = 351 余 12（对应 C）
   • 351 ÷ 13 = 27 余 0
   • 27 ÷ 13 = 2 余 1
   • 2 ÷ 13 = 0 余 2
2. 从下往上读取余数：
   得到十三进制数：210C。

分析：

• 对于每一个二进制位：
  • 如果 x和 y 的某一位都是 1，则：
    • x & y的该位为 1，
    • x ∣ y的该位为 1，
    • 和为 2（即 1+1）。
  • 如果某一位是 1 和 0：
    • x & y的该位为 0，
    • x ∣ y的该位为 1，
    • 和为 1（即 0+1）。
  • 如果某一位是 0 和 0：
    • 和为 0（即 0+0）。
• 因此，(x & y)+(x ∣ y) 的结果等于 x+y。

所以原式简化为：

x+y=2025

---

问题转化

我们需要找到最小的正整数 y 满足：

y=2025−x

且 yy必须满足：

1. y 是正整数（即 y≥1），
2. x≥0且 x<2025。

参考程序1

//暴力枚举，官方答案，我觉得官方答案有问题，因为它假设了y<=2025，如果要证明y<=2025，就应该按照上面的证明得到x+y=2025，就不需要再做按位计算。

#include <cstdio>

 using namespace std;

 int x;

 int main() {

    scanf("%d", &x);

for (int i = 1; i <= 2025; i++)

 if ((x & i) + (x | i) == 2025) {

 printf("%d\n", i);

 return 0;

 }

 printf("-1\n");

 return 0;

 }

参考程序2

#include <iostream>

using namespace std;

int findMinY(int x) {

    if (x < 0 || x >= 2025) {

        return -1; // x 超出范围，无解

    }

    int y = 2025 - x;

    return (y >= 1) ? y : -1;

}

int main() {

    int x;

    cin >> x;

    cout << findMinY(x) << endl;

    return 0;

}

参考程序

下面这是官方程序，没有参考意义，同学们按照自己想法写。

#include <bits/stdc++.h>

 using namespace std;

 int main() {

    int n; cin >> n; assert(1 <= n && n <= 100);

    map<string, int> cnt;

    int mx = -1;

    for (int i = 1; i <= n; i ++) {

        string s; cin >> s;

        assert(s.length() <= 30);

        transform(s.begin(), s.end(), s.begin(), ::tolower);

        if (! cnt.count(s))

            cnt[s] = 0;

        mx = max(mx, ++ cnt[s]);

    }

    int mx_num = 0;

    for (auto it = cnt.begin(); it != cnt.end(); it++)

        if ((it->second) == mx) {

            cout << (it->first) << '\n';

            mx_num ++;

        }

    assert(mx_num == 1);

    return 0;

 }

学编程、玩信奥，微信搜“信奥莫老师”，或关注微信公众号“AI之上-信奥驿站”