GESP 2025年3月C++ 6级 真题与解析

答案：D

解析：至少是可以被扩展的。

答案：B

解析：使用频率越高离根节点越近。

答案：A

解析：先根，然后左右，所以是前序遍历。

答案：B

解析：如果最后节点的两个叶子子节点都为空是可以的，有某一个叶子节点为空不可以，或跳过一个含空叶子节点的节点后还有其他叶子节点也不可以。

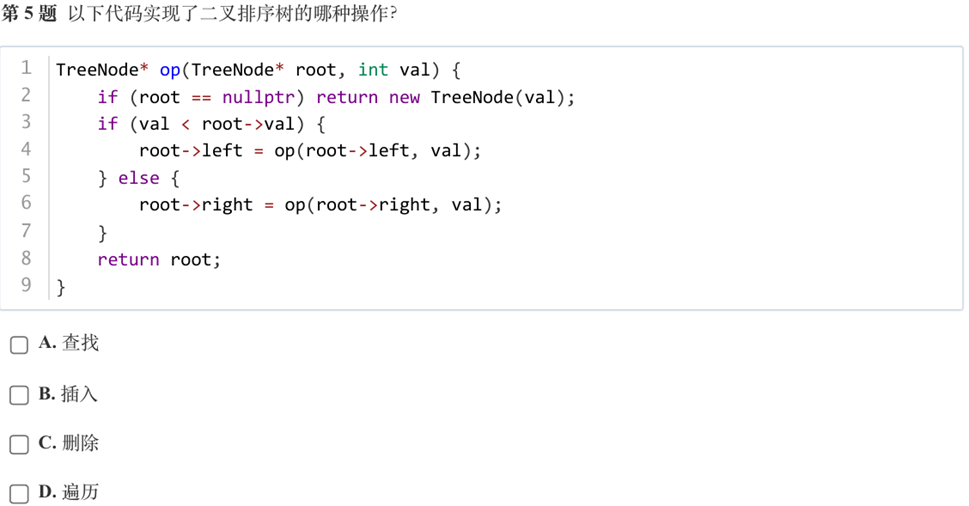
答案：B

解析：如果树为空，新节点就是根节点，否则就判断是否比当前节点小，小的放左边，大的放右边，所以是插入。

答案：B

解析：

答案：B

解析：A，动态规划不能和贪心直接比较。C，递归都需要存储中间结果。D，子问题必须重叠。

答案：A

解析：

关键点：

1. MyClass obj1;
   • 直接调用 默认构造函数 MyClass()，因此输出 "Constructor called!"。
   • 调用次数：1 次。
2. MyClass obj2 = obj1;
   • 这里执行的是 拷贝初始化，调用的是 拷贝构造函数（MyClass(const MyClass&)），而不是默认构造函数。
   • 由于代码中没有显式定义拷贝构造函数，编译器会自动生成一个隐式的拷贝构造函数（不会输出任何内容）。
   • 调用次数：1 次（但无输出）。

答案：A

解析：如代码，如果队列满了就返回false，如果为空就放第1个。

答案：A

解析：如果左节点不为空就将左节点入栈。

答案：A

解析：显而易见

答案：A

解析：n位格雷码有2n个编码，所以递归情况下可以分两种情况

1. 格雷码的递归生成规则：
   • n 位格雷码 的前半部分是 n-1 位格雷码 的每个编码前加 "0"。
   • 后半部分是 n-1 位格雷码的逆序，并在每个编码前加 "1"。
2. 代码逻辑：
   • 第一个 for 循环处理前半部分（"0" + prev[i]）。
   • 第二个 for 循环需要：
     • 逆序遍历 prev（i 从 prev.size() - 1 到 0）。
     • 在每个 prev[i] 前加 "1"，以保证相邻格雷码仅有一位差异。

示例（n=2）：

1. 递归调用 generateGrayCode(1) 返回 {"0", "1"}。
2. 前半部分："0" + "0" = "00"，"0" + "1" = "01" → {"00", "01"}。
3. 后半部分（逆序加 "1"）："1" + "1" = "11"，"1" + "0" = "10" → {"11", "10"}。
4. 最终结果：{"00", "01", "11", "10"}（符合 2 位格雷码）。

答案：B

解析：显而易见，在不放当前物品和放当前物品中选择最大值

答案：C

解析：如果最后栈里还有括号，就返回false。

答案：A

解析：shapePtr是指针，把地址付给它是可以的。

答案：T

解析：如题所述

答案：T

解析：相邻两个编码只有一位不同。

答案：F

解析：队列，先进先出

答案：T

解析：先左，然后根，最后右

答案：T

解析：如题所述

答案：F

解析：如果该节点不是整棵树的最左节点（即存在父节点使其位于某个右子树中），则它不是最小值。

答案：T

解析：如题所述，找不出更少的情况了。

答案：T

解析：如题所述。

答案：T

解析：这是一颗完全二叉树

答案：T

解析：如题所述。栈的插入删除都在双向链表的表头，队列的插入在链表尾部、删除在链表头部，所以每次操作都只有一步。

参考程序

// 官方答案用的单调队列，复杂度是O(n)，这段代码巧妙地结合了环形数组展开、前缀和和单调队列技术。

#include <cstdio>

#include <algorithm>

using namespace std;

const int N = 4e5 + 5;

int n;

long long a[N], pre[N];

int q[N], ql, qr;                               //q用来保存一个升序排序的当前最小前缀和对应a序列中的序号队列

long long ans;

int main() {

   scanf("%d", &n);

   for (int i = 1; i <= n; i++) {

       scanf("%lld", &a[i]);

       a[n + i] = a[i];                         // 为了方便处理环，将数组复制一份，因为环上不会重复访问，所以复制一份即可

   }

   for (int i = 1; i <= 2 * n; i++)

       pre[i] = pre[i - 1] + a[i];              // 前缀和，pre

   ql = qr = 1;                                 // ql和qr分别指向队列首尾

   ans = -1e18;

   for (int i = 1; i <= 2 * n; i++) {

       while (ql <= qr && q[ql] < i - n)        // 如果最小的前缀和对应的a序列中的序号q[ql]已经不在环上（i-n到i是环能覆盖的最大长度），那么就删除它

           ql++;                                

       ans = max(ans, pre[i] - pre[q[ql]]);     //pre[i] - pre[q[ql]] 是i到i-n区间内的最大值

       while (ql <= qr && pre[i] < pre[q[qr]])  // 如果当前前缀和比队尾小，那么就删除队尾，使得队列单调递增

           qr--;

       q[++qr] = i;                             // 将i加入队列

   }

   printf("%lld\n", ans);

   return 0;

}

// 普通方法复杂度是O(n^2)，会超时

// #include <cstdio>

// #include <algorithm>

// using namespace std;

// const int N = 4e5 + 5;

// int n;

// long long a[N], pre[N];

// int q[N], ql, qr;                               //q用来保存一个升序排序的当前最小前缀和对应a序列中的序号队列

// long long ans;

// int main() {

//    scanf("%d", &n);

//    for (int i = 1; i <= n; i++) {

//        scanf("%lld", &a[i]);

//        a[n + i] = a[i];                         // 为了方便处理环，将数组复制一份，因为环上不会重复访问，所以复制一份即可

//    }

//    for (int i = 1; i <= 2 * n; i++)

//        pre[i] = pre[i - 1] + a[i];              // 前缀和，pre

//    ans = -1e18;

//    for (int i=1;i<=2*n;i++){

//         for (int j=max(1,i-n);j<i;j++) {

//             ans = max(ans, pre[i] - pre[j]);

//         }

//    }

//    printf("%lld\n", ans);

//    return 0;

// }

学编程、玩信奥，微信搜“信奥莫老师”，或关注微信公众号“AI之上-信奥驿站”