排序算法与算法分析基础
输入:n个数(a1, a2, a3, …an)。
输出:输入序列的一个排列,重新排序(b1, b2, b3,…bn),满足b1<=b2<=b3<=…<=bn。
排序算法
插入排序(INSERTION_SORT)
首先是插入排序,这是一个针对少量元素排序的有效算法,很形象的是和我们在打牌时整理手中的牌的顺序差不多。先看一下它的伪代码:
key是当前待排序的数。
INSERTION_SORT(A) pseudocode
for j<--- 2 to length[A]
do key<---A[j]
//Insert A[j] into the sorted sequence A[1,2,...,j-1]
i<---j-1
while i>0 and A[i]>key
do A[i+1]<---A[i]
i<---i-1
A[i+1]<---key实现程序
#include<iostream>
#include<cstdio>
using namespace std;
void INSERTION_SORT(int *array, int size)
{
int key;
for(int i=1;i<size;++i)
{
key=*(array+i);
int j=i-1;
while((j>=0)&&(*(array+j)>=key))
{
*(array+j+1)=*(array+j);
--j;
}
*(array+j+1)=key;
}
}
int main()
{
int Num[10]={8,12,3,4,1,23,11,9,24,31};
INSERTION_SORT(Num,10);
for (int i=0;i<10;++i)
{
printf("%d\t",Num[i]);
}
cin.get();
return 0;
}合并排序(MERGE SORT)
有很多算法在结构上是递归的,通过一次或多次调用自身来递归解决相关问题。这些算法通常采用分治策略:将原问题划分为n个规模较小而结构与原问题相同的子问题,递归地解决这些子问题,然后再合并其结果,就得到了原问题的解。
分治模式在每一层递归上都有三个步骤:
- 分解:将原问题分解为一系列的子问题
- 解决:递归地解决各个子问题,若子问题足够小,则直接求解
- 合并:将子问题的解合并成原问题的解
合并排序算法完全依照了上述模式:
- 分解:将n个元素分解为各含n/2个元素的子序列
- 解决:用合并排序法对两个子序列递归地进行排序
- 合并:合并两个已排序的子序列得到结果
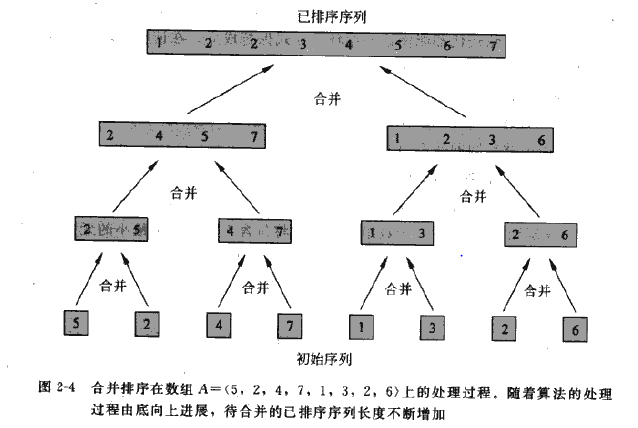
在对子序列进行排序时,长度为1时递归结束,单个元素认为是已经排好序的。合并排序的关键步骤在于排序过程中两个已排序好的序列的合并,在此引入一个子过程辅助合并MERGE(A,p,q,r),其中A是数组,p、q、r是数组的下标,满足p<=q<r,该过程实现两个已经排序好的数组A[p,q]、A[q+1,r]的合并。
MERGE(A,p,q,r)的时间代价是θ(n),n=r-p+1为元素的个数,因为最多进行n次比较。它的实现过程是:每次取两个序列中最小的元素(每个排序好的序列的第一个或者最后一个)进行比较,然后将两者中较小的一个按序放在输出数组中,重复此步骤直到某个序列被比较完。在程序的实现过程中,为了避免每次检查序列是否被比较完,在此引入“哨兵”的概念。在每个序列末尾添加一个哨兵,其包含一个特殊值,用来指示序列的结束(C++容器中就是用此概念标志容器的结束)。在这里用“∞”作为哨兵值,因为他不可能是两者中比较小的,除非是两个序列都到了结束的地方,而此时已经进行了n次比较,算法可以停止了。
MERGE(A,p,q,r)
A[p,q] n1<---q-p+1
A[q+1,r] n2<---r-q
//create arrays L[1,...,n1+1] and R[1,...,n2+1]
for i<---1 to n1
L[i]<---A[p+i-1]
for j<---1 to n2
R[j]<---A[q+j]
L[n1+1]<---∞
R[]n2+1<---∞
i<---1
j<---1
for k<---p to r
do if L[i]<=R[j]
then A[k]<---L[i]
i<---i+1
else A[k]<---R[j]
j<---j+1现在就可以把MERGE作为一个子过程用在MERGE_SORT过程中了,MERGE_SORT(A,p,r) 实现了对数组A[p…r]的排序。如果p>=r,则只有一个元素,就是已经排序好的了。若p<r,分解步骤就计算出下一个下标q,将A[p…r]分解为A[p…q]和A[q+1…r]。
MERGE_SORT(A,p,r)
if p<r
then q<---[(p+r)/2](向下取整)
MERGE_SORT(A,p,q)
MERGE_SORT(A,q+1,r)
MERGE(A,p,q,r)下图自底向上展示了当n为2的幂数时,整个过程的操作。算法将递归到每个序列元素为1,然后将两个长度为1的序列合并成已排序好的、长度为2的序列,接着又把两个长度为2的已排序的序列合并成长度为4的已排序好的序列。一直进行到将两个长度为n/2的已排序好的序列合并成长度为n的排序好的序列。
实现程序
#include<iostream>
#include<cmath>
#define INT_MAX 9999//~(1<<(sizeof(int)*8-1))
using namespace std;
void MERGE(int *array, int p, int q, int r)
{
int n1=q-p+1;
int n2=r-q;
int *L=new int[n1+1];
int *R=new int[n2+1];
for(int i=0;i!=n1;++i)
{
L[i]=*(array+p+i);
}
for(int i=0;i!=n2;++i)
{
R[i]=*(array+q+1+i);
}
L[n1]=INT_MAX;
R[n2]=INT_MAX;
for(int k=p,i=0,j=0;k!=r+1;++k)
{
if(L[i]<=R[j])
{
*(array+k)=L[i];
++i;
}
else
{
*(array+k)=R[j];
++j;
}
}
delete [] L;
delete [] R;
}
void MERGE_SORT(int *array, int p, int r)
{
if(p<r)
{
int q=floor((p+r)/2);
MERGE_SORT(array,p,q);
MERGE_SORT(array,q+1,r);
MERGE(array,p,q,r);
}
}
int main()
{
int Num[10]={8,12,3,4,1,23,11,9,24,31};
MERGE_SORT(Num,0,9);
for(int i=0;i!=10;++i)
{
cout<<Num[i]<<"\t"<<flush;
}
cin.get();
return 0;
}算法分析
算法分析指对一个算法所需要的资源进行预测。内存、通信带宽或者计算机硬件等资源是我们经常需要关心的,但一般资源指的是我们希望测度的计算时间。当采用RAM模型作为实现技术的时候,RAM包含了真实计算机中常见的指令:算术指令(加、减、乘、除、取余、向上取整、向下取整)、数据移动指令(装入、存储、复制等指令)和控制指令(条件和非条件转移、子程序调用和返回指令),其中每条指令所需的时间都为常量。
算法的运行时间指的是,在特定输入的情况下,所执行的基本操作数,可以方便地定义独立于机器的“步骤”的概念。采用以下观点:每个步骤执行都需要花费一定的时间,虽然每个步骤所需时间不同,但是我们假定每次执行第i行所花费的时间为常量ci。
插入排序分析

该算法的运行时间是所有语句执行的时间之和:
如果给定输入非常理想,序列都已经按序排列好,即对于每个j,A[j]都大于A[1,..,j-1],即 A[i]<key 恒成立,所以第6行和第7行没有执行过,对于第5行,由于 A[i]>key 不成立,所以 tj=1 。则算法最佳运行时间为:
可以表示为 an+b ,依赖于时间常量 ci ,为输入规模的线性函数。
而如果输入序列是逆序输入的,则会出现最坏的情况,A[1,…,j-1]都需要和key进行比较,因而对于j=2…n, tj=j ,此时最长的算法时间为:
此时运行时间为输入规模的二次函数。即最坏情况下其增长率为 θ(n2) 。
合并排序分析
当一个算法中含有对自身的递归调用时,其运行时间可以用一个递归方程来表示。该方程通过描述子问题与原问题之间的关系,来给出总的运行时间。
设
T(n)
为规模n的总的运行时间,假设我们把原问题分解为a个子问题,每一个子问题大小是原问题的1/b(对于合并算法,a=b=2,但是在许多其他分治算法中,a≠b),如果分解该问题和合并解的时间分别为
D(n)和C(n)
, 则:
在这里假定MERGE_SORT的输入规模为2的幂数,这样每一次分解所产生的序列长度都为n/2,考虑最坏情况下的运行时间:
- 分解:这一步仅仅是计算出了子数组的中间位置,需要常量时间,因此时间为θ(1);
- 解决:递归解决两个规模为n/2子问题,时间为 2T(n/2) ;
- 合并:进行n次比较赋值,因此时间为θ(n);
可将上式具体表示如下:
将递归扩展成一种等价树进行表示, cn 是树根, 2T(n/2) 是两个两颗子树,每一个子树节点的代价都是 cn/2 ,继续在树中扩展节点,直到问题规模降到了1。
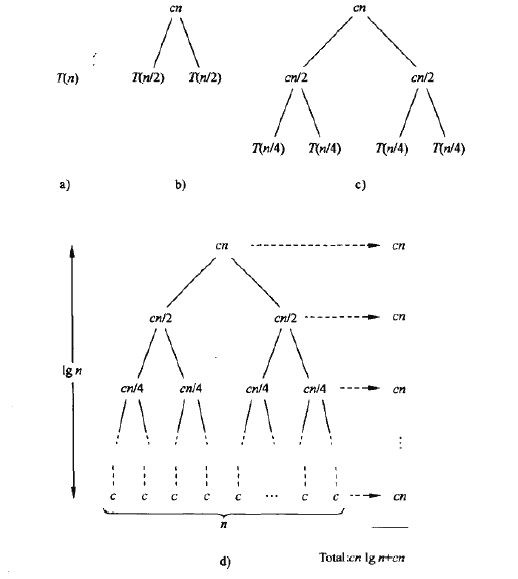
接下来给这棵树的每一层加上相应的代价,树根的代价为 cn ,下一层的两个节点的代价分别为 cn/2 。一般来说顶层之下第i拥有 2i 个节点,而相应的每个节点的代价为 (cn/2i) ,因而每层的总代价都为 cn 。”递归树“中总的层数为 lgn+1 ,比如n为2时,树有2层。在该树中,每一层的代价为 cn ,层数为 lgn+1 ,所以总的代价为:
忽略低阶项和常量项,可得到其时间增长率为 θ(nlgn) 。也就是说但规模n达到一定程度时,最坏情况下的合并排序也比最佳情况下的插入排序速度要快( lgn 比任何线性函数都要增长的慢)。
算法真是一个神奇而又强有力的利器,特别是在用到递归算法的时候感触特别深,一个递归运算可以精简多少行代码啊。这只是对算法有一个初步的认识,下面将要深入学习一下算法设计过程中的循环不变式,当算法复杂到一定程度时,使用循环不变式对算法进行分析论证是不可避免的。
祝枫
2016年7月4日于深圳
























 324
324

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








