主成分分析(PCA)——矩阵角度推导

1. 写在前面

最近机器学习课上正式讲了主成分分析，只是老师说的很快，我并没有完全理解。随后我搜了很多关于这方面的讲解来进行理解，仅CSDN上就有很多讲的很好的文章，从协方差矩阵角度进行说明，基本上我也都理解了。但另一方面我发现可以结合我最近学的矩阵分析，从纯矩阵运算的角度推导。这里说明在阅读这篇文章之前，最好对矩阵知识有一定的了解，不过不用多深，因为我才刚刚开始学矩阵分析，所以我对矩阵的了解也不深。

2. 简单示例

在进一步推导公式什么的之前，我希望先通过一个简单的例子来具象化对PCA的理解。虽然数学概念是抽象的，但是它发挥作用的地方就在我们身边，特别是机器学习的概念知识。首先PCA是干什么的呢？它是用来降低输入的维度的，因为维度太高实在是不好分析，而且也没办法具象地显示出来。那怎么降低输入矩阵的维度呢，直接把其中的几个维度删掉吗？那这样的话，删掉哪几个呢？肯定不是直接删掉其中的维度，万一把关键的输入信息给删掉了，就算降低维度了，这个错误的输入还有什么用呢？PCA的思想是把输入的点投影到几个正交轴上，这里的轴就代表着维度，如果可以在删掉其中几个轴的同时还保留原来的大部分信息，那么这个降维就成功了。这是如何做到的呢？下面我们来看一个例子：

假如平面内存在三个坐标点，它们分别是(1,2), (2,4)和(3,6)。显然在这种情况下要表示这三个点我们得有两个维度，也就是(1,0)和(0,1)。如果我们换一个维度，这三个点还是这样表示吗？我们令新的维度是(1,2)，(2,-1)。上述三个坐标点就变成了(1,0)，(2,0)和(3,0)。可以看到在第二个维度下，三个点的坐标都是0，也就是说这三个点在第二个维度上没有一点变化，如果我们删掉第二个维度，原本三个坐标点的坐标信息是完全被保留了的，这也蕴含了PCA的主要思想：换基底。

很多时候，人往往会忽略司空见惯的东西，把一切都当做是理所当然。当我们写下每个数字的时候，我们往往会以十进制的角度去考虑它们，同样在我们标出点的坐标的时候我们也会以(1,0)和(0,1)为基底去表示它们。但是，这并不是理所当然的，坐标的位置并不会因为我们选取的基底而改变，我们选取(1,0)和(0,1)最直接的考量是这样表示简单，但情况并不总是这样。正如上述的例子，如果我们换一个基底表示这些点，坐标会变得更加简单。

3. 正式推导

通过上面的说明，我想大家应该对基底变换和它的作用有了更加具象的理解，下面我们要把具象的示例抽象出来，用数学语言进行表达。考虑一个输入矩阵：

这个矩阵表明输入的特征维度是n，共有m个样本。其实当我写出这个矩阵的时候，就已经隐含了一个信息，即这是以单位矩阵为基底的矩阵，因此每个样本的特征可以这样表示

整体就是：

注意，这里的X是原来输入矩阵的转置。到这里可能你会觉得好笑，你写的这不是废话吗？就像写1=1这么无聊。好，下面我们要换个基底，在新的基底下表示X，这个新的基底也要是个单位正交矩阵，那么就有：

代入上面的例子，输入矩阵是

显然有，这里为了简单我就没把I'单位化了，是需要要单位化的，这样使

因此我们有：

这里

在新的基底下，每个样本点在某一个维度上的投影或者坐标就从原来的

变成了

PCA的想法是能够在删除维度的同时尽可能保留更多的信息。还记得我们上面的示例吗？如果我们能让点投影到某个维度上之后，它原本的信息仅通过这个维度就可以尽可能地进行保存，那么去掉其他维度就不会损失什么信息。如何实现这点呢？其实这是个线性回归的问题，即找到一个直线的使所有点到该直线距离平方和最小，这样我们可以说这个方向已经尽力做到了最好，保留了尽可能多的信息。

到这个直线距离的平方和最小，其实也就是投影到这个方向上坐标的平方和最大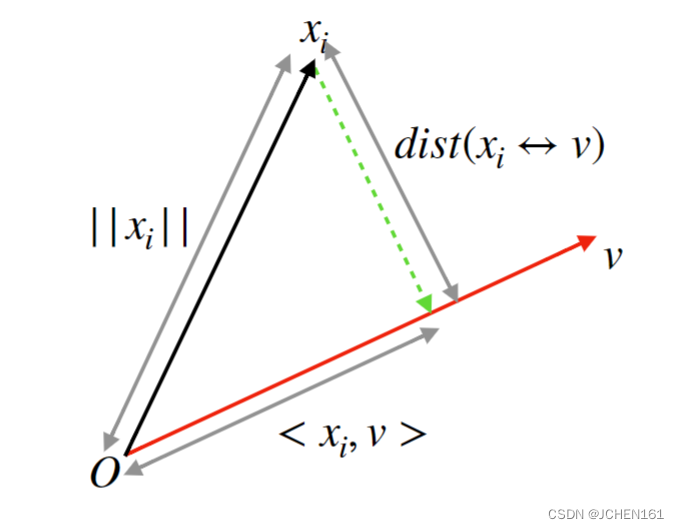

我们知道投影到任一维度的坐标是

如何使其平方和达到最大呢？首先我们得想办法表示这个出这个平方和。我们有：

显然我们关注的平方和是这个矩阵的主元，即

这步如果不太懂请仔细看看矩阵方面的知识，需要灵活掌握矩阵维度的表示。

由于是对称矩阵，有

U为正交矩阵，是对角矩阵，主元为特征值，从大到小依次排列，U是特征值对应的特征向量组成的矩阵。

同样是正交矩阵。

因此我们要使上式达到最大有：

根据拉格朗日乘子法可解得：

那么此时我们就找到了第一个我们要的方向，就是U的第一列，即的最大特征值对应的特征向量。我们先把所有点投影到这个方向上，可以保留最多的信息。可能你会奇怪为什么这里的变成了第一个方向，这是因为坐标系轴的方向是相对的而不是绝对的，我在这里用表示新基底的向量是想表明通用性。找到第一个方向了，第二个方向该如何找呢？首先我们知道：

因为互相正交，所以有

可得，此时约束方程就变成了

 

此时有

同理我们可以接着找下面的方向，你会发现每个向量就是相应特征值对应的特征向量，X是已知的，我们也可以解得特征值和特征向量，所以就解出来了，对应的在新的基底下的X的表示也可以求出，至此结束。

4. 结语

可以看到，与其他文章从协方差矩阵角度出发不同的是，上面的过程我并没提到方差，就是通过矩阵运算，附带用拉格朗日乘子法求最值来进行求解。但目前还存在一个问题，就是我发现在求解完成之后我其实并没有去中心化，也就是我上面的输入矩阵必须要减去均值才能完全对上其他文章从协方差矩阵出发的结果。那么在这里，为什么要减去均值呢？总之，我认为矩阵分析是非常值得研究和学习的，HORN的矩阵分析教材我十分推荐，非常值得阅读，也顺带批评一下国内的线代教材，写的实在一言难尽（本人工科，入门矩阵知识就是通过线代）。