ZKP价值链路的垂直整合

mutourend

已于 2024-05-09 16:10:16 修改

阅读量1.0k

点赞数 36

分类专栏：零知识证明文章标签：零知识证明

于 2024-04-02 22:38:02 首次发布

本文链接：https://blog.csdn.net/mutourend/article/details/137293608

版权

零知识证明专栏收录该内容

348 篇文章

订阅专栏

1. ZKP proof生命周期

从ZKP（zero-knowledge proof）生命周期，先看围绕ZKP的价值链路形成：
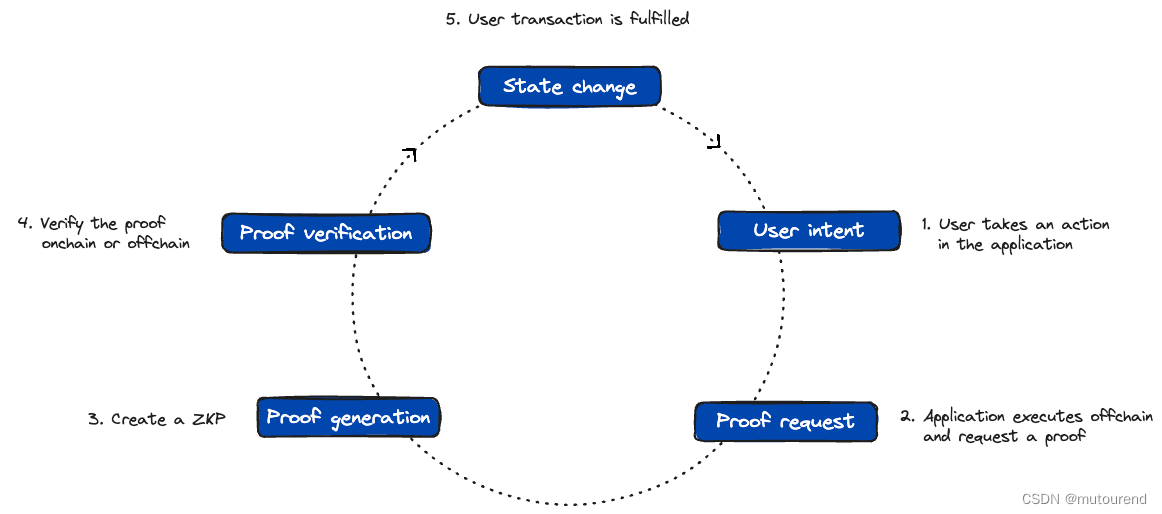
在这里插入图片描述

1）User intent用户意图：以某用户意图为起点，如想要在某zk-rollup上swap某token、证明其身份、执行某衍生品交易等等。
2）Proof request请求生成证明：应用执行交易，通常是在某zkVM（zero-knowledge virtual machine）内，并请求proof。
3）Proof generation生成证明：生成proof是计算密集型的。应用开发者可使用自己的prover，也可将该工作外包给第三方provers，如Succinct Labs、Gevulot、Bonsai等。
4）Verification验证：一旦proof生成，需在链上或链下进行验证。若在链上验证，则该应用在某目标链上运行某合约，该合约的任务是验证该proof。
5）Settlement结算：一旦proof在链上验证通过，则结算完成。此时，该应用在目标链上的其它模块可使用该proof来更新该应用的状态。

以简单的bridge为例：

1）用户要想将10 USDC从源链SC 发送到目标链DC。
2）用户在SC的某bridge合约内锁定token，且bridge app在链下生成proof。
3）该proof在DC的验证合约内验证通过后，DC上的另一合约为该用户释放10 USDC。

以上简化的ZKP proof生命周期，有助于理解ZKP价值链路的垂直整合。

2. ZKP proof价值链路

与以太坊内的区块构造类似，基础设施栈及其价值链正在形成，有参与者在专门负责该流程的每一步：
在这里插入图片描述
其中：

1）zkVMs：首先是一个由编程语言和开发者平台组成的生态系统，用于生成证明。由于证明是复杂的密码学工具，因此需要简化开发人员的体验。RISC Zero或SP-1等开发人员平台是 zkVM：使开发人员可以轻松生成用于一般计算的 ZKP，从而无需关心底层复杂电路。在后台，其本质上是将任意代码编译成可证明的电路。
2）Prover markets：应用程序可以生成自己的证明，但其最终目标是使用去中心化的provers网络来抵抗审查并确保服务不会崩溃（活性）。可自己运行prover set，就像区块链对其validator set所做的那样，但这项工作很可能由Succinct Labs、Bonsai或Gevulot等Prover markets承担。
3）Proof aggregation：网络生成的证明需要验证。目前，通过L1或L2区块链上的合约来完成的proof验证，很贵。最便宜的证明（Groth16）在以太坊上的证明成本为 20-30 美元（假设 3000 美元 ETH 和 30 Gwei）。 STARK 证明的费用为 180 美元。
这是证明使用的关键瓶颈，因此出现了一类新兴的解决方案，其重点是降低验证成本。主要方法是证明聚合。直觉是将多个证明组合成一个证明。该单一证明可以证明所有原始证明的有效性，因此可以分摊所有rollup证明的成本。
4）Proof settlement：证明无论是否聚合，都需要在链上进行验证才能在智能合约中使用。目前这是在 L1 和 L2 上完成的，但对专注于降低验证成本并实现proof-generating应用程序之间的互操作性的专用层的前景感到兴奋。
5）Application：该价值链的最后一部分是用户进行交易和支付服务费用的应用程序。这是资金流动的起点，并在价值链中向前流动。

3. 价值点何在？

价值链的多个点具有网络效应和防御性。

1）Application应用层拥有用户，因此拥有“proof订单流”。这是一种被逼入绝境的资源，尤其是在用户数量有限的加密领域。
2）zkVM开发者平台。受益于使用其zkVM开发者平台的应用程序开发人员的一些锁定。这也赋予了其对订单流的一些权力，因为无论与谁集成，都将从其生成的proof流中受益。
3）proof market具有强大的网络效应。其工作是将证明请求与可生成proof的服务提供商相匹配。更高的需求会吸引更多的计算资源供应商进行证明，从而形成典型的市场良性循环。进一步的规模经济使flywheel变得更加复杂，因为数量意味着更高的利用率，从而降低成本。期望围绕这一层进行集中化，并且已经看到了激烈的竞争。
4）Proof verification证明验证是更新兴的一层，但也受益于强大的网络效应。聚合随着数量而扩展：必须聚合的证明越多，成本和延迟就越低（因为在其他条件相同的情况下，假设每个证明的成本固定，可以更快地完成batches）。
5）Settlement结算也随着数量的增加而扩展：如果所有证明都在一个地方结算，那么该层就可以成为证明的规范事实来源，从而成为一个无需信任的互操作层。

4. 价值栈的上扩和下沉

期望价值链实现垂直化，并且已经看到公司为此目的增加了其功能，从一层开始，并寻求在价值栈上向上和向下进行集成。
在这里插入图片描述

RISC Zero 最初是一个 zkVM，让开发人员为 Rust 和 C++ 代码生成证明。然后，建立了 Bonsai，一个证明市场，代表用户生成证明。这是一个巨大的协同效应，因为RISC Zero拥有“proof订单流”，且可引导它自己的市场。编译并没有特别的差异化或防御性，但proof market是一个引人注目的价值累积层。
Succinct Labs 也朝相反的方向做了同样的举动。其最初是一个证明市场。然后迅速添加了证明聚合层，并通过创建 SP-1（一种开源 zkVM）来向价值栈上扩，以与 RISC Zero 竞争。尽管不了解其决策，但将 zkVM 层商品化是有意义的，以确保像 Risc-0 这样的单一参与者不会拥有proof订单流并规避其proof market。Succinct Labs 最近还通过添加的聚合层来下沉价值栈，以进一步从其“proof订单流”中受益。
像 Polygon 这样具有大量未使用区块空间的目标链也希望从聚合开始，在价值栈上上扩。