全同态加密理论、生态现状与未来展望（中1）

《全同态加密理论、生态现状与未来展望》系列由lynndell2010@gmail.com和mutourend2010@gmail.com整理原创发布，分为上中下三个系列：

• 全同态加密理论、生态现状与未来展望（上）：专注于介绍全同态加密理论知识。
• 全同态加密理论、生态现状与未来展望（中1）：专注于介绍全同态加密四代算法中第一代第二代FHE算法的衍化历程。
• 全同态加密理论、生态现状与未来展望（中2）：专注于介绍全同态加密四代算法中第三代第四代FHE算法的衍化历程。
• 全同态加密理论、生态现状与未来展望（下）：专注于介绍当前全同态加密生态现状及未来展望。

整个系列内容可能存在纰漏，希望能得到大家的反馈，有任何问题欢迎邮件联系lynndell2010@gmail.com和mutourend2010@gmail.com，或在本文下方评论留言。

3. 四代全同态加密

3.1 第1代：基于理想格和AGDC

Gentry09的方案涉及了较多的代数数论，方案复杂度较高。
DGHV10方案基于整数，方案简单，便于理解，但计算复杂度高，公钥尺寸非常大。

3.1.1 Gentry09

Fully homomorphic encryption using ideal lattices

理想：$I$是环$R$的一个子集，包含0（即加法的逆元素），满足以下条件：

• $I$中两个元素的加法结果仍然在 $I$ 中；

• $I$中的一个元素与$R$中的一个元素的乘积仍然在$I$中。

主理想是由一个元素生成的理想，即由$a$生成的主理想是$a$的倍数组成的集合。

Gentry09方案： 使用由理想$I$定义的整数子格$L(I)\subseteq {\mathbb{Z}}^m$。

• 密钥生成： 公钥$B_{pk}$和私钥$B_{sk}$分别是理想格$L(I)$的劣质基与优质基。

• 加密： 消息是一比特， m ∈ { 0 , 1 } m \in \{0, 1\} m∈{0,1}），如下计算
  $$\mathbf{a}=m+2\mathbf{e}\in {\mathbb{R}}^d$$
  其中，$\mathbf{e}$是噪声，即一个随机向量，其系数属于 { 0 , ± 1 } \{0, \pm1\} {0,±1}，且 $\pm 1$ 取值的概率相等。
  密文$\mathbf{c}$是点$\mathbf{a}$在平行六面体$P(B_{pk})$中的平移。其中，$B_{pk}$ 是公钥，即
  $$\mathbf{c}=\mathbf{a}-(\lceil \mathbf{a}{B}_{pk}^{-1}\rfloor B_{pk})$$
  其中，$\lceil \cdot \rfloor$ 表示四舍五入到最近的整数。

• 解密： 计算
  $${\mathbf{a}}^{\prime }=\mathbf{c}-(\lceil \mathbf{c}{B}_{sk}^{-1}\rfloor B_{sk})$$
  这表示将$\mathbf{c}$平移到平行六面体 $\mathcal{P}(B_{sk})$。其中，$B_{sk}$ 是私钥。

  然后输出 ${\mathbf{a}}^{\prime }\mathrm{mod}2$ 作为解密后的明文。

上述方案由于解密算法的复杂性（即无法同态评估）而无法进行引导自举（bootstrapping 同态解密）。

为了解决该问题，Gentry提出了一个方法，通过对原始的同态加密方案$E$进行变换，得到一个新的方案$E^{\ast }$。该方案具有相同的同态能力，但具有一个简化的解密函数，从而允许bootstrapping。

为了降低解密算法的复杂性，Gentry证明只需在评估密钥中添加一些关于私钥的"额外信息"。这些额外信息由一组向量 S = { s i ∣ i = 1 , … , S } S = \{s_i | i = 1, \dots, S\} S={si​∣i=1,…,S} 组成，从中导出一个子集 $T$。私钥$sk$是$T$元素的和，评估密钥中包含的公钥信息是集合$S$。该新方案$E^{\ast }$的安全性基于：集合$T$是稀疏的且是私有的，因此适用稀疏子集和困难问题（SSSP）。

该方案的安全性基于4个困难问题：

1. 稀疏子集和困难问题（SSSP）： 已知$n$个整数 S = { a 1 , . . . , a n } ⊆ Z S=\{a_1,...,a_n\} \subseteq \mathbb{Z} S={a1​,...,an​}⊆Z，判断是否存在集合$S$的子集$I$，满足${\sum }_{i\in I}{a}_i=0$。

2. 有界距离解码困难问题（CVP困难问题的变形）： 已知一个目标向量 $\mathbf{t}$，使得 $\text{dist}(\mathbf{t},L)<\alpha {\lambda }_1(L)$。其中，${\lambda }_1(L)$ 是格$L$的第一个最短基向量的长度。求与$\mathbf{t}$最接近的一个格向量$\mathbf{v}\in L$。

3. 理想最短向量困难问题（SVP困难问题的变形）： 在格 $L$ 中找到一个最短的非零向量。其中，${\lambda }_1(L)$ 是 $\gamma {\lambda }_1(L)<{\lambda }_2(L)$ 且 $\gamma \ge 1$。换句话说，最短向量的长度保证至少是 ${\lambda }_2(L)$ 的 $\gamma$ 倍小。

4. 循环安全，文中未给出证明。

安全问题： CDPR16发现了使用主理想方案的一个漏洞：在给定一个量子多项式时间，或经典的$2^{n^{2/3-\epsilon }}$时间算法的情况下，可以进行密钥恢复攻击，攻击目标是基于主理想格的加密构造。Recovering Short Generators of Principal Ideals in Cyclotomic Rings

图3：基于理想格的方案汇总

3.1.2 DGHV10

Fully homomorphic encryption over the integers

该方案是1.2.4节方案实例的一般化

• 密钥生成： 私钥为$p$，即一个奇数随机整数，以及公钥 $(x_0,\dots ,x_n)$。$x_0$ 是奇数，且 $x_0>x_i,\forall i$
  $$x_i=p{q}_i+r_i$$
  $q_i,r_i$ 是随机整数。

• 加密： 消息 $m\in {\mathbb{F}}_2$ ，如下计算
  $$c=(m+2r+2\sum _{i\in S}{x}_i)\mathrm{mod}{x}_0$$
  其中，$r$ 是一个随机整数，$S$ 是 { 1 , … , n } \{1, \dots, n\} {1,…,n} 的一个随机子集。

• 解密： 计算$(c\mathrm{mod}p)\mathrm{mod}2$

该方案的安全性基于稀疏子集和问题（SSSP）以及近似最大公约数（AGCD）困难问题。

• SSSP困难问题： 已知$n$个整数 S = { a 1 , . . . , a n } ⊆ Z S=\{a_1,...,a_n\} \subseteq \mathbb{Z} S={a1​,...,an​}⊆Z，判断是否存在集合$S$的子集$I$，满足${\sum }_{i\in I}{a}_i=0$。

• AGCD困难问题： 已知随机选择的整数集 { x 0 , … , x n } ∈ Z \{x_0, \dots, x_n\} \in \mathbb{Z} {x0​,…,xn​}∈Z，求解"共同近似除数" $p$。
  
  图 4: 基于 AGCD 困难问题的 FHE 方案汇

3.2 第2代：基于LWE和RLWE

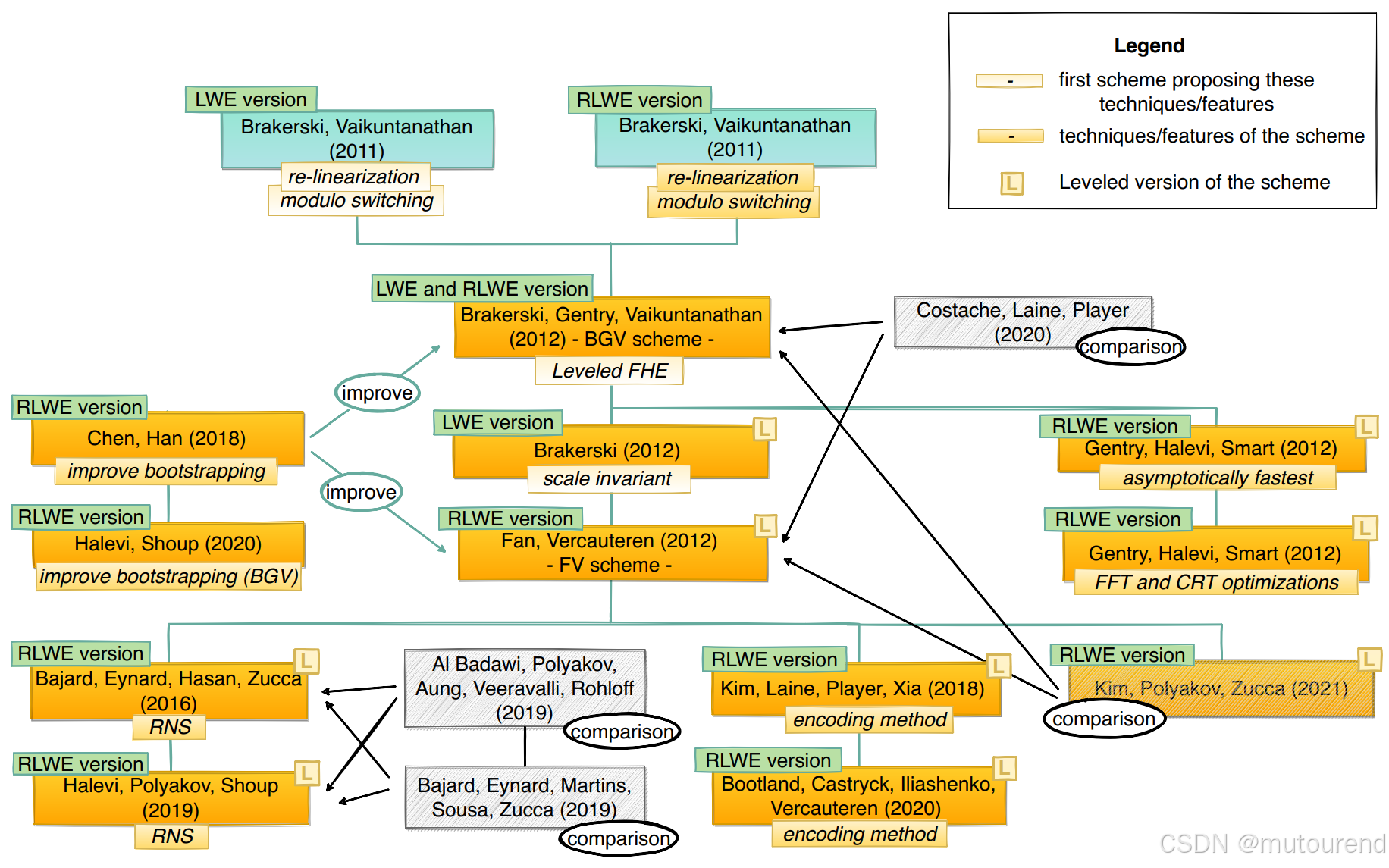
图 5: 第 2 代 FHE：基于 LWE 和 RLWE

3.2.1 预备知识：Kronecker Product

Wikipedia: Kronecker Product

• 张量积是向量积$\mathbf{a}\otimes \mathbf{b}$；

• Kronecker积是矩阵积$\mathbf{A}\otimes \mathbf{B}$。

Kronecker积有以下9个性质，最后2个是矩阵性质。

1. $A\otimes (B+C)=A\otimes B+A\otimes C$，要求$B$和$C$相同尺寸

2. $(A+B)\otimes C=A\otimes C+B\otimes C$，要求$A$和$B$相同尺寸

3. $kA\otimes B=A\otimes kB=k(A\otimes B)$

4. $(A\otimes B)\otimes C=A\otimes (B\otimes C)$

5. $(A\otimes B)(C\otimes D)=(AC)\otimes (BD)$

6. $(A\otimes B{)}^T=A^T\otimes B^T$

7. $(A\otimes B{)}^{-1}=A^{-1}\otimes B^{-1}$

8. $A\otimes B\ne B\otimes A$

9. $B\otimes A=P(A\otimes B)Q$, $P$和$Q$是置换矩阵

10. $(AB{)}^T=B^T{A}^T$，矩阵性质

11. $(AB{)}^{-1}=B^T{A}^{-1}$，矩阵性质

3.2.2 BV11

Efficient Fully Homomorphic Encryption from (Standard) LWE

• 密钥生成： 选择随机数$\mathbf{s}\in {\mathbb{Z}}_q^n$，则私钥为$\bar{\mathbf{s}}=(-\mathbf{s},1)\in {\mathbb{Z}}_q^{n+1}$。

• 加密： 消息为$m\in {\mathbb{F}}_2$，选择随机矩阵$\mathbf{A}\in {\mathbb{Z}}_q^{m\times n}$和噪声$e\in {\mathbb{Z}}_q^n$，$e$从误差分布$\chi$中随机选择的，计算
  $$\mathbf{c}=(\mathbf{A},b=⟨\mathbf{A},\mathbf{s}⟩+2\mathbf{e}+m)\in {\mathbb{Z}}_q^{m\times n}\times {\mathbb{Z}}_q^n$$
  则密文为$\mathbf{c}=(\mathbf{A},\mathbf{b})$。

• 解密： 输入私钥$\bar{\mathbf{s}}=(-\mathbf{s},1)$和密文$\mathbf{c}=(\mathbf{A},\mathbf{b})$，如下计算
  $$\begin{array}{rl}& ⟨\mathbf{c},\bar{\mathbf{s}}⟩=(\mathbf{b}-⟨\mathbf{A},\mathbf{s}⟩\mathrm{mod}q)\mathrm{mod}2\\ & =\left((⟨\mathbf{A},\mathbf{s}⟩+2\mathbf{e}+m)-⟨\mathbf{A},\mathbf{s}⟩\mathrm{mod}q\right)\mathrm{mod}2\end{array}$$

• 同态加法： $$\begin{array}{rl}& \mathbf{c}+{\mathbf{c}}^{\prime }=(\mathbf{A},\mathbf{b})+({\mathbf{A}}^{\prime },{\mathbf{b}}^{\prime })\\ & =(\mathbf{A}+{\mathbf{A}}^{\prime },⟨\mathbf{A},\mathbf{s}⟩+2\mathbf{e}+m+⟨{\mathbf{A}}^{\prime },\mathbf{s}⟩+2{\mathbf{e}}^{\prime }+m^{\prime })\\ & =(\mathbf{A}+{\mathbf{A}}^{\prime },⟨\mathbf{A}+{\mathbf{A}}^{\prime },\mathbf{s}⟩+2(\mathbf{e}+{\mathbf{e}}^{\prime })+m+m^{\prime })\\ & =({\mathbf{A}}^{\prime \prime },⟨{\mathbf{A}}^{\prime \prime },\mathbf{s}⟩+2{\mathbf{e}}^{\prime \prime }+m^{\prime \prime })\\ & =({\mathbf{A}}^{\prime \prime },{\mathbf{b}}^{\prime \prime })\\ & ={\mathbf{c}}^{\prime \prime }\end{array}$$
  其中，$m^{\prime \prime }=m+m^{\prime }$。注意，${\mathbf{e}}^{\prime \prime }=\mathbf{e}+{\mathbf{e}}^{\prime }$
  噪声有积累。同态加法情况下影响较小。

• **解密：**输入私钥$\bar{\mathbf{s}}=(-\mathbf{s},1)$和密文${\mathbf{c}}^{\prime \prime }=({\mathbf{A}}^{\prime \prime },{\mathbf{b}}^{\prime \prime })$，如下计算
  $$m+m^{\prime }:=⟨{\mathbf{c}}^{\prime \prime },\overline{\stackrel{ˉ}{\mathbf{s}}}⟩=({\mathbf{b}}^{\prime \prime }-⟨{\mathbf{A}}^{\prime \prime },\mathbf{s}⟩\mathrm{mod}q)\mathrm{mod}2$$

• 同态乘法：$\mathbf{c}\otimes {\mathbf{c}}^{\prime }$，称为Kronecker积（Kronecker Product），是外积/张量积从向量到矩阵的推广

• 解密： 私钥$\bar{\mathbf{s}}$扩展为新私钥$\bar{\mathbf{s}}\otimes \bar{\mathbf{s}}$。注意：私钥长度增加了。
  如下计算 $$\begin{array}{rl}& ⟨\mathbf{c}\otimes {\mathbf{c}}^{\prime },\bar{\mathbf{s}}\otimes \bar{\mathbf{s}}⟩\\ & =(\mathbf{c}\otimes {\mathbf{c}}^{\prime }{)}^T(\bar{\mathbf{s}}\otimes \bar{\mathbf{s}})\\ & =({\mathbf{c}}^T\otimes {\mathbf{c}}^{\prime T})(\bar{\mathbf{s}}\otimes \bar{\mathbf{s}})\\ & =({\mathbf{c}}^T\bar{\mathbf{s}})\otimes ({\mathbf{c}}^{\prime T}\bar{\mathbf{s}})\\ & =⟨\mathbf{c},\bar{\mathbf{s}}⟩\otimes ⟨{\mathbf{c}}^{\prime },\bar{\mathbf{s}}⟩\\ & =⟨\mathbf{c},\bar{\mathbf{s}}⟩\cdot ⟨{\mathbf{c}}^{\prime },\bar{\mathbf{s}}⟩\\ & =m\cdot m^{\prime }\end{array}$$

其中，等号1：内积；等号2：性质6；等号3：性质5；等号4：内积；等号5：Kronecker内积退化；等号6：常规解密。

论文引入了2种新技术：再线性化和维度模缩小。

• 再线性化是必要的，以将乘法密文大小从接近 $n^2/2$
  降到常规大小，即
  $n+1$。为了实现这一减少，通过"加密"对称密钥的所有项来转换
  $c_1\cdot c_2$
  的二次方程为线性方程。随后，Brakerski、Gentry和Vaikuntanathan
  (Leveled) Fully Homomorphic Encryption without Bootstrapping
  将这一技术称为密钥交换（key switching）。在3.2.4节阐述。

• 维度模缩小，即模交换技术，将同态加密方案（SHE）转换为完全同态加密方案，通过将密文 $c$ 对模 $q$ 的取模转换为密文 $c^{\prime }$ 对模 $p$ 的取模。其中，$p$ 比 $q$ 小得多。具体而言，先将 ${\mathbb{Z}}_q$ 中的每个元素乘以 $p/q$，然后取最近的整数。此操作的一个有趣副作用是密文中的误差减少。由于采用了模切换，噪声增长较低，这使得可以同态评估解密电路，而无需Gentry提出的压缩方法，使得SSSP假设不再是必需的。在3.2.5节阐述。

3.2.3 BGV14

(Leveled) fully homomorphic encryption without bootstrapping

设 $d$ 为 2 的幂，$q$ 为奇正整数模数，$\chi$ 为 R 上的误差分布。其中，$R=\mathbb{Z}[x]/⟨x^d+1⟩$。 设 $B$ 为 $\chi$ 输出元素长度的界限（以极高的概率），并且 $B$ 被设置为尽可能小以保持安全性。 对于任意自然数 $p$，$R_p={\mathbb{Z}}_p[x]/⟨x^d+1⟩$。该方案的工作流程如下：

• 密钥生成： 输入安全参数 $\lambda$，随机选择一个小的秘密元素 $s\in \chi$，并设置私钥$sk=\mathbf{s}=(1,s)\in R_q^2$。随机均匀生成一个 $a^{\prime }\in R_q$，然后计算 $b=a^{\prime }s+2e$。其中，$e$ 是从 $\chi$ 中随机选择的误差。 输出 $sk$ 和公钥 $pk=\mathbf{a}=(b,-a^{\prime })$。以下等式成立
  $$⟨\mathbf{a},\mathbf{s}⟩=⟨(b,-a^{\prime }),(1,s)⟩=⟨(a^{\prime }s+2e,-a^{\prime }),(1,s)⟩=2e$$

• 加密： 输入公钥$pk\in R_q^2$ 和消息 $m\in R_2$，将 $m$ 转换为向量 $\mathbf{m}=(m,0)\in R_q^2$，并选择噪声$r,e_0,e_1\in \chi$。输出密文为
  $$\mathbf{c}=\mathbf{m}+2(e_0,e_1)+\mathbf{a}r$$ 展开为：
  $$\mathbf{c}=(c_0,c_1)=(m+2e_0+br,2e_1-a^{\prime }r)\in R_q^2$$

• 解密： 输入私钥$s\in R_q^2$ 和密文 $\mathbf{c}\in R_q^2$，计算内积 $$\begin{array}{rl}& ⟨\mathbf{c},\mathbf{s}⟩=c_0+c_{1}s\\ & =m+2e_0+br+(2e_1-a^{\prime }r)s\\ & =m+2e_0+(a^{\prime }s+2e)r+(2e_1-a^{\prime }r)s\\ & =m+2e_0+2e_{1}s+2er\end{array}$$ 并输出 $((m+2(e_0+e_{1}s+er))\mathrm{mod}q)\mathrm{mod}2=m$。
  注意：解密能正常工作是因为 $e,e_0,e_1$ 和 $s$ 足够小（因为它们是 $\chi$ 的元素）。

• 同态加法： 对应相加 $$\begin{array}{rl}& \mathbf{c}+{\mathbf{c}}^{\prime }=(c_0,c_1)+(c_0^{\prime },c_1^{\prime })\\ & =(m+2e_0+br,2e_1-a^{\prime }r)+(m^{\prime }+2e_0^{\prime }+b{r}^{\prime },2e_1^{\prime }-a^{\prime }{r}^{\prime })\\ & =\left(m+m^{\prime }+2(e_0+e_0^{\prime })+b(r+r^{\prime }),2(e_1+e_1^{\prime })-a^{\prime }(r+r^{\prime })\right)\\ & =\left(m^{\prime \prime }+2e_0^{\prime \prime }+b{r}^{\prime \prime },2e_1^{\prime \prime }-a^{\prime }{r}^{\prime \prime }\right)\\ & =(c_0^{\prime \prime },c_1^{\prime \prime })\\ & ={\mathbf{c}}^{\prime \prime }\end{array}$$

• 解密： $$\begin{array}{rl}& ⟨{\mathbf{c}}^{\prime \prime },\mathbf{s}⟩=c_0^{\prime \prime }+c_1^{\prime \prime }s\\ & =m^{\prime \prime }+2e_0^{\prime \prime }+b{r}^{\prime \prime }+(2e_1^{\prime \prime }-a^{\prime }{r}^{\prime \prime })s\\ & =m^{\prime \prime }+2e_0^{\prime \prime }+(a^{\prime }s+2e)r^{\prime \prime }+(2e_1^{\prime \prime }-a^{\prime }{r}^{\prime \prime })s\\ & =m^{\prime \prime }+2e_0^{\prime \prime }+2e_1^{\prime \prime }s+2e{r}^{\prime \prime }\end{array}$$ 再$\mathrm{mod}q\mathrm{mod}2$，则获得$m^{\prime \prime }=m+m^{\prime }$。

  因此，只要结果中的误差不与模数$q$重叠，解密就能正常工作。

• 同态乘法： $\mathbf{c}\otimes {\mathbf{c}}^{\prime }$

• 解密： 私钥$\mathbf{s}$扩展为新私钥$\mathbf{s}\otimes \mathbf{s}$。注意：私钥长度增加了。如下解密：
  $$\begin{array}{rl}& ⟨\mathbf{c}\otimes {\mathbf{c}}^{\prime },\mathbf{s}\otimes \mathbf{s}⟩\\ & =(\mathbf{c}\otimes {\mathbf{c}}^{\prime }{)}^T(\mathbf{s}\otimes \mathbf{s})\\ & =({\mathbf{c}}^T\otimes {\mathbf{c}}^{\prime T})(\mathbf{s}\otimes \mathbf{s})\\ & =({\mathbf{c}}^T\mathbf{s})\otimes ({\mathbf{c}}^{\prime T}\mathbf{s})\\ & =⟨\mathbf{c},\mathbf{s}⟩\otimes ⟨{\mathbf{c}}^{\prime },\mathbf{s}⟩\\ & =⟨\mathbf{c},\mathbf{s}⟩\cdot ⟨{\mathbf{c}}^{\prime },\mathbf{s}⟩\\ & =m\cdot m^{\prime }\end{array}$$

3.2.4 核心技术：密钥交换

解密分析： $$\begin{array}{rl}& ⟨\mathbf{c}\otimes {\mathbf{c}}^{\prime },\mathbf{s}\otimes \mathbf{s}⟩\\ & =⟨\mathbf{c},\mathbf{s}⟩\cdot ⟨{\mathbf{c}}^{\prime },\mathbf{s}⟩\\ & =(c_0+c_{1}s)(c_0^{\prime }+c_1^{\prime }s)\\ & =c_0{c}_0^{\prime }+(c_0{c}_1^{\prime }+c_1{c}_0^{\prime })s+c_1{c}_1^{\prime }{s}^2\\ & =d_0+d_{1}s+d_2{s}^2\\ & =⟨(d_0,d_1,d_2),(1,s,s^2)⟩\end{array}$$
解密过程可以看系数为$(d_0,d_1,d_2)$的多项式，在横坐标$s$处的求值。
存在问题： 私钥$\mathbf{s}$扩展为新私钥$\mathbf{s}\otimes \mathbf{s}$，同态乘法一次，则需要私钥扩展一次。
解决方案： 将$s^2$加密到$s$下，可实现密文中的$d_2{s}^2$转换为${\bar{c}}_0+{\bar{c}}_{1}s$。
具体而言，令消息$m=s^2$，则$\mathbf{m}=(s^2,0)$。

选择随机数$r,e_0,e_1\in \chi$，如下加密：
$$\mathbf{c}=(s^2,0)+2(e_0,e_1)+(b,-a^{\prime })r=(s^2+2e_0+br,-(a^{\prime }r-2e_1))\approx (s^2+\alpha s,-\alpha )=(\beta ,-\alpha ).$$
其中，$\alpha =a^{\prime }r-2e_1$，$s^2+2e_0+br=s^2+2e_0+(a^{\prime }s+2e)r=s^2+2e_0+a^{\prime }sr+2er\approx s^2+a^{\prime }rs-2e_{1}s=s^2+\alpha s$，仅去掉了$2e_0$。
因此，$s^2\approx \beta -\alpha s$，使得扩展密文$(d_0,d_1,d_2)$变成一个正常密文$(\overline{c_0},\overline{c_1})$。
$$d_0+d_{1}s+d_2{s}^2=d_0+d_{1}s+\beta -\alpha s=(d_0+\beta )+(d_1-\alpha )s=\overline{c_0}+\overline{c_1}s$$

• 扩展密文$\mathbf{c}\otimes {\mathbf{c}}^{\prime }=(c_0,c_1)\otimes (c_0^{\prime },c_1^{\prime })=(d_0,d_1,d_2)$，对应的扩展私钥为$\mathbf{s}\otimes \mathbf{s}=(1,s,s^2)$。

• 正常密文$(\overline{c_0},\overline{c_1})$，对应的正常密钥为$\mathbf{s}=(1,s)$。

因此，密钥交换技术把扩展密文变成了正常密文，使得解密密钥不变。

3.2.5 核心技术：模交换

同态乘法： $$\begin{array}{rl}& \mathbf{c}\otimes {\mathbf{c}}^{\prime }=(c_0,c_1)\otimes (c_0^{\prime },c_1^{\prime })=(c_0{c}_0^{\prime },c_0{c}_1^{\prime },c_1{c}_0^{\prime },c_1{c}_1^{\prime })\\ & =(m+2e_0+br)(m^{\prime }+2e_0^{\prime }+b{r}^{\prime })+(m+2e_0+br)(2e_1^{\prime }-a^{\prime }{r}^{\prime })\\ & +(m^{\prime }+2e_0^{\prime }+b{r}^{\prime })(2e_1-a^{\prime }r)+(2e_1-ar)(2e_1^{\prime }-a^{\prime }{r}^{\prime })\end{array}$$ 噪声为$(r,e_0,e_1),(r^{\prime },e_0^{\prime },e_1^{\prime })\in \chi$

存在问题： 有两个噪声值为$||\chi ||$的密文，相乘后噪声近似为$||\chi |{|}^2$，则经过$\log k$层同态乘法，噪声积累就达到上限$||\chi |{|}^k\mathrm{mod}q$，则不能继续运算了。

解决方案： 每次同态乘法运算完后对噪声乘以$1/||\chi ||$，则噪声减低为$||\chi ||$。此时模缩减为$q/||\chi ||$。因此，模每缩减一次，则可以进行$\log k$层同态乘法运算。相比原来，仅能进行$\log k$层同态乘法，是指数级提高。

3.2.6 FV12

Somewhat Practical Fully Homomorphic Encryption

令 $R=\mathbb{Z}[x]/⟨x^d+1⟩$。其中，$d$ 是 2 的幂。令 $q$ 和 $p$ 为正整数，令放大因子$\Delta =\lfloor q/p\rfloor$ 和 $r_t(q)=q\mathrm{mod}p$。对于任何自然数 $t$，令$R_t={\mathbb{Z}}_t[x]/⟨x^d+1⟩$。令 $\chi$ 是 $R_q$ 上的 B 有界概率分布。FV方案的如下：

• 密钥生成： 输入安全参数 $\lambda$，输出小的随机数作为私钥 $sk=s\in \chi$。选择随机数$a\in R_q$，并计算 $-(a\cdot s+e)\mathrm{mod}q$。其中，$e\in \chi$ 是噪声。输出$sk=s\in \chi$和 $pk=(p_0,p_1)=(-(a\cdot s+e)\mathrm{mod}q,a)$。

• 加密： 输入消息 $m\in R_p$ 和公钥 $pk\in R_q^2$。选择小的随机数$u,e_1,e_2\in \chi$，如下计算：
  $$\begin{array}{rl}& c_0=(p_0\cdot u+e_1+\Delta \cdot m)\mathrm{mod}q,\\ & c_1=(p_1\cdot u+e_2)\mathrm{mod}q\end{array}$$ 输出密文 $c=(c_0,c_1)$。

• 解密： 输入秘密密钥 $s\in R_q$ 和密文 $c\in R_q^2$，如下解密
  $$m:=c(s)=\lceil \frac{p\cdot (c_0+c_1\cdot s)\mathrm{mod}q}{q}\rfloor \mathrm{mod}p$$
  公式展开： $$\begin{array}{rl}& \frac{p[c_0+c_1\cdot s]\mathrm{mod}q}{q}\\ & =\frac{p[p_0\cdot u+e_1+\Delta \cdot m+p_1\cdot u\cdot s+e_2\cdot s]\mathrm{mod}q}{q}\\ & =\frac{p[-(a\cdot s+e\cdot )u+e_1+\Delta \cdot m+a\cdot u\cdot s+e_2\cdot s]\mathrm{mod}q}{q}\\ & =\frac{p[\Delta \cdot m+e\cdot u+e_1+e_2\cdot s]\mathrm{mod}q}{q}\\ & =\frac{[q\cdot m+pe\cdot u+p{e}_1+p{e}_2\cdot s]\mathrm{mod}q}{q}\\ & =m+\frac{p[e\cdot u+e_1+e_2\cdot s]\mathrm{mod}q}{q}\end{array}$$
  密文$c$被视为在$s$处评估的多项式，即$c(s)$，而不是一个具有两个分量的向量。

• 同态加法：$c+c^{\prime }=(c_0+c_0^{\prime },c_1+c_1^{\prime })=(c_0^{\prime \prime },c_1^{\prime \prime })$

• 解密： $$\begin{array}{rl}& \frac{p[c_0^{\prime \prime }+c_1^{\prime \prime }\cdot s]\mathrm{mod}q}{q}\\ & =\frac{p[(c_0+c_0^{\prime })+(c_1+c_1^{\prime })\cdot s]\mathrm{mod}q}{q}\\ & =\frac{p[(p_0\cdot u+e_1+\Delta \cdot m+p_1\cdot u\cdot s+e_2\cdot s)+(p_0\cdot u^{\prime }+e_1^{\prime }+\Delta \cdot m^{\prime }+p_1\cdot u^{\prime }\cdot s+e_2^{\prime }\cdot s)]\mathrm{mod}q}{q}\\ & =\frac{p[-(a\cdot s+e\cdot )(u+u^{\prime })+(e_1+e_1^{\prime })+\Delta \cdot (m+m^{\prime })+a\cdot (u+u^{\prime })\cdot s+(e_2+e_2^{\prime })\cdot s]\mathrm{mod}q}{q}\\ & =\frac{p[\Delta \cdot (m+m^{\prime })+e\cdot (u+u^{\prime })+(e_1+e_1^{\prime })+(e_2+e_2^{\prime })\cdot s]\mathrm{mod}q}{q}\\ & =\frac{[q\cdot (m+m^{\prime })+pe\cdot (u+u^{\prime })+p(e_1+e_1^{\prime })+p(e_2+e_2^{\prime })\cdot s]\mathrm{mod}q}{q}\\ & =(m+m^{\prime })+\frac{p[e\cdot (u+u^{\prime })+(e_1+e_1^{\prime })+(e_2+e_2^{\prime })\cdot s]\mathrm{mod}q}{q}\end{array}$$

• 同态乘法： $c\otimes c^{\prime }=(c_0{c}_0^{\prime },c_0{c}_1^{\prime },c_1{c}_0^{\prime },c_1{c}_1^{\prime })$

• 解密： 两个密文的乘积给出的结果是一个二次多项式：
  $$\begin{array}{rl}& c(s)\cdot c^{\prime }(s)\\ & =(c_0+c_1\cdot s)\cdot (c_0^{\prime }+c_1^{\prime }\cdot s)\\ & =c_0{c}_0^{\prime }+(c_0{c}_1^{\prime }+c_1{c}_0^{\prime })s+c_1{c}_1^{\prime }\cdot s^2\\ & ={\alpha }_0+{\alpha }_1\cdot s+{\alpha }_2\cdot s^2\\ & ={\beta }_0+{\beta }_1\cdot s\end{array}$$ 最后一步是密钥交换。

3.2.7 LTV13

On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption

• 密钥生成： 选择两个小的随机多项式 $f^{\prime },g\in \chi$。其中，$\chi$是$R=\mathbb{Z}[x]/⟨x^d+1⟩$上的B有界分布，且$d$是2的幂。私钥为$f=2f^{\prime }+1\in R$。其中，$f\equiv 1\mathrm{mod}2$，且 $f$ 在 $R_q$ 中是可逆的。 公钥为$h=2g{f}^{-1}\mathrm{mod}q\in R_q$。

• 加密： 输入消息为$m\in {\mathbb{F}}_2$，随机小元素$r,e\in \chi$，如下计算
  $$c=m+hr+2e\in R_q$$
  则密文$c$是卷积多项式环$R_q={\mathbb{Z}}_q[x]/⟨x^d+1⟩$中的一个元素。

• 解密： 输入私钥$f$和密文$c$，如下解密 $$\begin{array}{rl}& (fc\mathrm{mod}q)\mathrm{mod}2\\ & =f(m+hr+2e)\mathrm{mod}q\mathrm{mod}2\\ & =fm+fhr+2fe\mathrm{mod}q\mathrm{mod}2\\ & =fm+2(gr+fe)\mathrm{mod}q\mathrm{mod}2\\ & =fm+2v\mathrm{mod}q\mathrm{mod}2\\ & =(2f^{\prime }+1)m+2v\mathrm{mod}2\\ & =m\end{array}$$ 存在一个关键等式： $$fc=mf+2v\in R_q$$

3.2.8 核心技术：提升维数

上述环LEW加密方案中，私钥的维数为$k$，令$l=\lceil \log q\rceil$。其中，$q$是加密方案的模，则$\text{powerof2}(sk)$的维数为$kl$。

• 加密： 消息为$m\in {\mathbb{F}}_2$，如下加密：
  $$\begin{array}{l}{\mathrm{c}}_{1,1}:={\mathrm{Enc}}_{\mathrm{pk}}(\mathrm{m},0,...,0),...,{\mathrm{c}}_{1,\mathrm{l}}:={\mathrm{Enc}}_{\mathrm{pk}}(\mathrm{m}\cdot 2^{\mathrm{l}-1},0,...,0)\\ {\mathrm{c}}_{2,1}:={\mathrm{Enc}}_{\mathrm{pk}}(0,\mathrm{m},0,...,0),...,{\mathrm{c}}_{2,\mathrm{l}}:={\mathrm{Enc}}_{\mathrm{pk}}(0,\mathrm{m}\cdot 2^{\mathrm{l}-1},0,...,0)\\ ...\\ {\mathrm{c}}_{k,1}:={\mathrm{Enc}}_{\mathrm{pk}}(0,...,0,\mathrm{m}),...,{\mathrm{c}}_{\mathrm{k},\mathrm{l}}:={\mathrm{Enc}}_{\mathrm{pk}}(0,...,0,\mathrm{m}\cdot 2^{\mathrm{l}-1})\end{array}$$
  则密文是$kl\times k$的矩阵。

• 解密： 使用私钥对密文矩阵中的某个密文解密即可。

3.2.9 LTV13：维数提升+位展开

• 加密： 输入消息为$m\in {\mathbb{F}}_2$，随机小元素$r_i,e_i\in \chi$，如下计算
  $$c_i=m\cdot 2^i+h{r}_i+2e_i\in R_q$$
  则密文$\mathbf{c}=(c_1,...,c_l)\in R_q^l$。

• 解密： 输入私钥$f$和密文中的第一项$c_1$，如下解密
  $$\begin{array}{rl}& (f{c}_1\mathrm{mod}q)\mathrm{mod}2\\ & =f(m+h{r}_1+2e_1)\mathrm{mod}q\mathrm{mod}2\\ & =fm+fh{r}_1+2f{e}_1\mathrm{mod}q\mathrm{mod}2\\ & =fm+2(g{r}_1+f{e}_1)\mathrm{mod}q\mathrm{mod}2\\ & =fm+2v\mathrm{mod}q\mathrm{mod}2\\ & =(2f^{\prime }+1)m+2v\mathrm{mod}2\\ & =m\end{array}$$ 存在一个关键等式： $$f{c}_1=mf+2v\in R_q$$
  对关键等式一般化： $$f\mathbf{c}=(c_{1}f,...,c_{l}f{)}^T=(mf+2v,...,m\cdot 2^{i}f+2v)=m\cdot \text{Powersof2}(f{)}^T+2v\in R_q$$

• 同态加法：$\mathbf{c}+{\mathbf{c}}^{\prime }\in R_q^l$

• 解密： 先忽略$\mathrm{mod}q\mathrm{mod}2$ $$\begin{array}{rl}& f(\mathbf{c}+{\mathbf{c}}^{\prime })\\ & =f\mathbf{c}+f{\mathbf{c}}^{\prime }\\ & =(m\cdot \text{Powersof2}(f{)}^T+2v)+(m^{\prime }\cdot \text{Powersof2}(f{)}^T+2v^{\prime })\\ & =(m+m^{\prime })\cdot \text{Powersof2}(f{)}^T+2v+2v^{\prime }\end{array}$$ 取第一个元素，就是明文。

• 同态乘法：
  $\text{BitDecomp}(\mathbf{c})\bullet \mathbf{c}\in R_q^l$

• 解密： $$\begin{array}{rl}& (\text{BitDecomp}(\mathbf{c})\bullet {\mathbf{c}}^{\prime })f\\ & =\text{BitDecomp}(\mathbf{c})\cdot (m^{\prime }\cdot \text{Powersof2}(f{)}^T+2v^{\prime })\\ & =m^{\prime }\mathbf{c}f+2v^{\prime }\text{BitDecomp}(\mathbf{c})\\ & =m^{\prime }(m\cdot \text{Powersof2}(f{)}^T+2v)+2v^{\prime }\text{BitDecomp}(\mathbf{c})\\ & =m^{\prime }m\cdot \text{Powersof2}(f{)}^T+2v{m}^{\prime }+2v^{\prime }\text{BitDecomp}(\mathbf{c})\end{array}$$

去掉噪声，取出明文$m{m}^{\prime }$。

相关方案发展脉络如图6所示。

图 6: 第 2 代 FHE：基于 NTRU

参考文献

• GGH公钥密码系统 Public-key cryptosystems from lattice reduction problems

• Regev05论文On Lattices, Learning with Errors, Random Linear Codes, and Cryptography

• Brakerski12论文Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP

• Micciancio-Regev书 Lattice-based cryptography

• KTX07论文Multi-bit Cryptosystems Based on Lattice Problems

• DGHV10论文Fully homomorphic encryption over the integers

• LV10论文On Ideal Lattices and Learning with Errors over Rings

• Gentry09论文Fully homomorphic encryption using ideal lattices

• CR16论文Recovering Short Generators of Principal Ideals in Cyclotomic Rings

• BV11论文Efficient Fully Homomorphic Encryption from (Standard)LWE

• LTV13论文On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption

• GSW13论文Homomorphic Encryption from Learning with Errors:Conceptually-Simpler, Asymptotically-Faster, Attribute-Based

• TRLWE18论文TFHE: Fast Fully Homomorphic Encryption over the Torus

• 陈智罡 全同态加密：从理论到实践

• 周福才、徐剑 格理论与密码学

• Google Jeremy Kun 2024.5博客 A High-Level Technical Overview of Fully Homomorphic Encryption

• Optalysys团队2024年10月博客 Fully Homomorphic Encryption industry leaders join forces to form global FHE Hardware Consortium

• Fhenix团队2023年10月17日博客 The Holy Grail of Encryption: The Rise of FHE Technology

• NGC Ventures团队2024年1月12日博客 Introduction to FHE and Blockchain: Implications for Scalability and Privacy

• Awesome Fully Homomorphic Encryption (FHE) x Blockchain resources, libraries, projects, and more

• Awesome Homomorphic Encryption

• PANews 2024年9月17日文章 全同态加密（FHE）的进展与应用

• 2022年论文《Survey on Fully Homomorphic Encryption, Theory, and Applications》

• Craig Gentry 2022年论文《Homomorphic encryption: a mathematical survey》

• 2024年12月20日Jorge Myszne，Niobium Microsystems 首席产品官 博客 3 Homomorphic Encryption Trends for 2025

• HCLTech团队2024年6月研报 Homomorphic encryption: Exploring technology trends and future approach

• 2024年论文《vFHE: Verifiable Fully Homomorphic Encryption》

• PPS Lab团队2023年10月博客 Arithmetizing FHE in Circom

• PPS Lab团队2023年10月博客 A primer on the FHEW & TFHE schemes

• 2024年论文《Oraqle: A Depth-Aware Secure Computation Compiler》

• 2023年10月论文《A Survey on Implementations of Homomorphic Encryption Schemes》

• Sunscreen团队2021年8月博客 An Intro to Fully Homomorphic Encryption for Engineers

• TFHE：2016年论文《Faster Fully Homomorphic Encryption: Bootstrapping in less than 0.1 Seconds》

• BGV：2011年论文 《Fully Homomorphic Encryption without Bootstrapping》

• BFV：2012年论文《Somewhat Practical Fully Homomorphic Encryption》

• CKKS：2016年论文《Homomorphic Encryption for Arithmetic of Approximate Numbers》

• HomomorphicEncryption.org 2018年slide Building Applications with Homomorphic Encryption

• Greenfield Capital 2024年7月博客 The muted Seven – 7 things you should consider re confidential compute

• Sunscreen 2023年8月博客 How SNARKs fall short for FHE

• 2024年4月18日BigBrainVC团队博客 Flawed Homomorphic Encryption

• 2024年Verisense Network slide An Introduction To FHE and Its Application in Rust

• Vitalik 2020年7月20日博客 Exploring Fully Homomorphic Encryption

• 2023年论文《Verifiable Fully Homomorphic Encryption》

• 2018年《Homomorphic Encryption Standard v1.1》

• 2021年论文《SoK: Fully Homomorphic Encryption Compilers》

• 2024年论文《SoK: Fully Homomorphic Encryption Accelerators》

• Sunscreen团队2023年5月博客 Building an FHE compiler for the real world

• Zama团队2023年5月23日博客 Private Smart Contracts Using Homomorphic Encryption

• Craig Gentry 2024年6月分享视频 FHE: Past, Present and Future