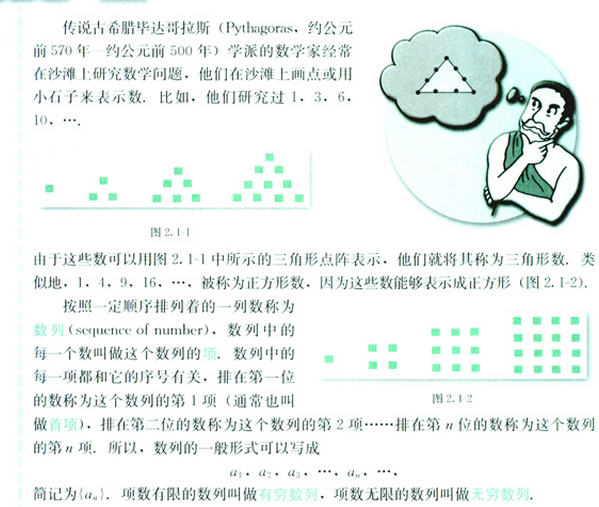
剧情提要:
[机器小伟]在[工程师阿伟]的陪同下进入了结丹后期的修炼,
这次要修炼的目标是[数列]。



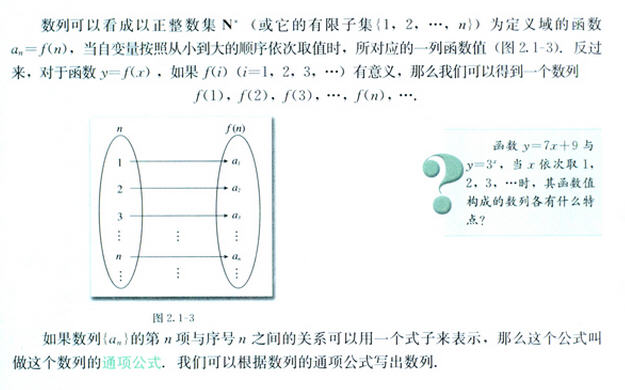
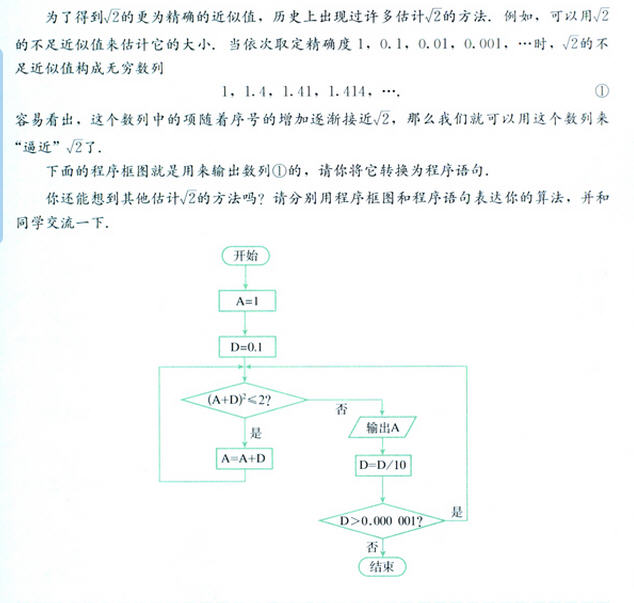
那么这个面积到底是多大呢?
应该是18
[机器小伟]在[工程师阿伟]的陪同下进入了结丹后期的修炼,
这次要修炼的目标是[数列]。
正剧开始:
星历2016年04月16日 16:00:58, 银河系厄尔斯星球中华帝国江南行省。
[工程师阿伟]正在和[机器小伟]一起研究[数列]。
[人叫板老师]用了这种表示人文关怀的绿色标关键字,真是有一种恰得其反的效果,
小伟要用放大镜才能看出这写的是啥呀。
<span style="font-size:18px;">>>>
1
1
2
3
5
8
13
21
34
55
89
144
233
377
610
987
1597
2584
4181
6765
----- 20 -----
def fib(N):
if (N < 2):
return 1;
else:
return fib(N-1)+fib(N-2);
def tmp():
for i in range(1000):
a = fib(i);
if (a > 10000):
print('-----', i, '-----');
break;
print(a);
</span>
这可以说是求值的最没效率的算法了。
<span style="font-size:18px;">>>>
1.4
1.41
1.414
1.4142
1.41421
1.414213
def sqrt2():
a = 1;
D = 0.1;
prec = 1;
while (D > 0.000001):
while (a+D)*(a+D) <= 2:
a += D;
print(round(a, prec));
D/=10;
prec+=1;
def tmp():
sqrt2();</span>
<span style="font-size:18px;"> if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0,190);
//坐标轴设定
var scaleX = 2*r, scaleY = 2*r;
var spaceX = 2, spaceY = 4;
var xS = -10, xE = 10;
var yS = -10, yE = 20;
config.axisSpacing(xS, xE, spaceX, scaleX, 'X');
config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');
var array = [];
var a0 = 1, d = 4, aN = a0;
for (var i = 0; i < 5; i++) {
array.push([i, aN]);
aN += d;
}
var size = array.length;
var transform = new Transform();
var tmp = [];
array = transform.scale(transform.translate(array, 0, 0), scaleX/spaceX, scaleY/spaceY);
tmp = [].concat(array);
vectorDraw(tmp, 'red');
tmp = [].concat(array);
shape.pointDraw(tmp, 'orange', 1, 1);
plot.setFillStyle('blue');
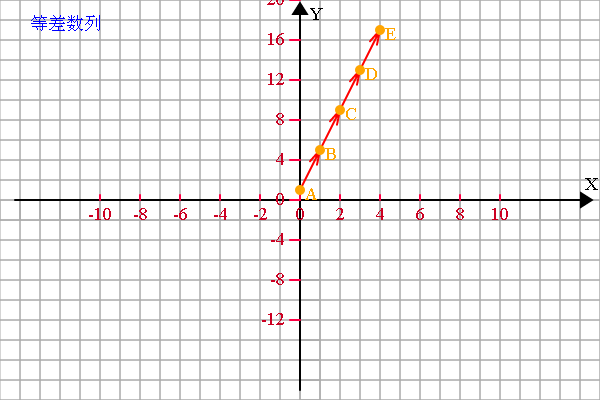
plot.fillText('等差数列', -270, -170, 300);
}</span>
<span style="font-size:18px;">>>>
等差数列: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100]
前100项和是:5050
#等差数列
def arithmeticSequence(a0, d, N):
seq = [];
for i in range(N):
seq.append(a0);
a0 += d;
print('等差数列: ', seq);
print('前{0}项和是:{1}'.format(N, sum(seq)));
def tmp():
a0 = 1;
d = 1;
N = 100;
arithmeticSequence(a0, d, N);
</span>
<span style="font-size:18px;">>>>
等差数列: [500, 550, 600, 650, 700, 750, 800, 850, 900, 950]
前10项和是:7250
def tmp():
a0 = 500;
d = 50;
N = 10;
arithmeticSequence(a0, d, N);</span>
<span style="font-size:18px;">>>>
当N取9时, 和已经会开始变小了。由19.999999999999993 -> 19.285714285714278。
#等差数列
def arithmeticSequence(a0, d, N):
seq = [];
for i in range(N):
seq.append(a0);
a0 += d;
#print('等差数列: ', seq);
#print('前{0}项和是:{1}'.format(N, sum(seq)));
return sum(seq);
def tmp():
a0 = 5;
d = 4+2/7-5;
result = [];
N = 1;
result.append(arithmeticSequence(a0, d, N));
while (N < 10):
N+=1;
result.append(arithmeticSequence(a0, d, N));
if (result[-1] < result[-2]):
print('当N取{0}时, 和已经会开始变小了。由{1} -> {2}。'.format(N, result[-2], result[-1]));
break;</span>
<span style="font-size:18px;">>>>
等比数列: [1, 0.84, 0.7055999999999999, 0.5927039999999999, 0.4978713599999999]
前5项和是:3.6361753599999997
#等比数列
def geometricSequence(a0, q, N):
seq = [];
for i in range(N):
seq.append(a0);
a0 *= q;
print('等比数列: ', seq);
print('前{0}项和是:{1}'.format(N, sum(seq)));
#return sum(seq);
def tmp():
a0 = 1;
q = 0.84;
N = 5;
geometricSequence(a0, q, N);</span>
<span style="font-size:18px;"> if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0,190);
//坐标轴设定
var scaleX = 4*r, scaleY = 2*r;
var spaceX = 2, spaceY = 0.25;
var xS = -10, xE = 10;
var yS = -1, yE = 1;
config.axisSpacing(xS, xE, spaceX, scaleX, 'X');
config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');
var array = [];
var a0 = 1, q = 0.81, aN = a0;
for (var i = 0; i < 8; i++) {
array.push([i, aN]);
aN *= q;
}
var size = array.length;
var transform = new Transform();
var tmp = [];
array = transform.scale(transform.translate(array, 0, 0), scaleX/spaceX, scaleY/spaceY);
tmp = [].concat(array);
vectorDraw(tmp, 'red');
tmp = [].concat(array);
shape.pointDraw(tmp, 'orange', 1, 1);
plot.setFillStyle('blue');
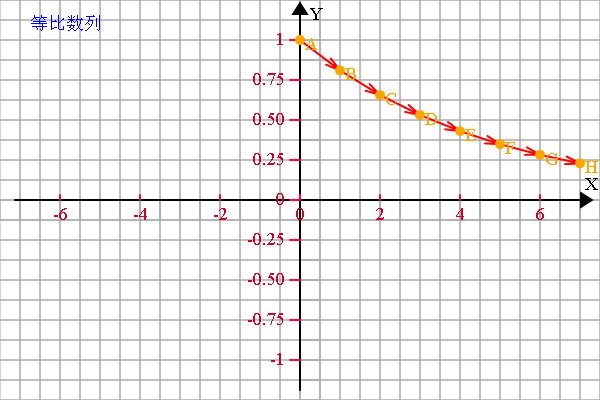
plot.fillText('等比数列', -270, -170, 300);
}
</span>

<span style="font-size:18px;">>>>
等比数列: [0.5, 0.25, 0.125, 0.0625, 0.03125, 0.015625, 0.0078125, 0.00390625]
前8项和是:0.99609375
等比数列: [27, -9.0, 3.0, -1.0, 0.3333333333333333, -0.1111111111111111, 0.037037037037037035, -0.012345679012345678]
前8项和是:20.246913580246915
>>> 1/243
0.00411522633744856
>>> 1640/81
20.246913580246915
#等比数列
def geometricSequence(a0, q, N):
seq = [];
for i in range(N):
seq.append(a0);
a0 *= q;
print('等比数列: ', seq);
print('前{0}项和是:{1}'.format(N, sum(seq)));
#return sum(seq);
def tmp():
a0 = 1/2;
q = 0.5;
N = 8;
geometricSequence(a0, q, N);
a0 = 27;
q = -math.pow(1/243/a0, 1/8);
N = 8;
geometricSequence(a0, q, N);
</span>
<span style="font-size:18px;">>>>
输入划分的块数N, N越大结果越准确:3
k, aN, sum = 1, 8.0, 8.0
k, aN, sum = 2, 5.0, 13.0
>>> ================================ RESTART ================================
>>>
输入划分的块数N, N越大结果越准确:10
k, aN, sum = 1, 2.673, 2.673
k, aN, sum = 2, 2.592, 5.265000000000001
k, aN, sum = 3, 2.457, 7.722
k, aN, sum = 4, 2.268, 9.99
k, aN, sum = 5, 2.025, 12.015
k, aN, sum = 6, 1.7280000000000002, 13.743
k, aN, sum = 7, 1.377, 15.120000000000001
k, aN, sum = 8, 0.9720000000000001, 16.092000000000002
k, aN, sum = 9, 0.5129999999999997, 16.605
def tmp():
sum_ = 0;
k = 1;
N = int(input('输入划分的块数N, N越大结果越准确:'));
while k<=N-1:
aN = (9-math.pow((k*3/N), 2))*3/N;
sum_ += aN;
print('k, aN, sum = {0}, {1}, {2}'.format(k, aN, sum_));
k+=1;
</span><span style="font-size:18px;">>>>
输入划分的块数N, N越大结果越准确:16
k, aN, sum = 1, 1.680908203125, 1.680908203125
k, aN, sum = 2, 1.6611328125, 3.342041015625
k, aN, sum = 3, 1.628173828125, 4.97021484375
k, aN, sum = 4, 1.58203125, 6.55224609375
k, aN, sum = 5, 1.522705078125, 8.074951171875
k, aN, sum = 6, 1.4501953125, 9.525146484375
k, aN, sum = 7, 1.364501953125, 10.8896484375
k, aN, sum = 8, 1.265625, 12.1552734375
k, aN, sum = 9, 1.153564453125, 13.308837890625
k, aN, sum = 10, 1.0283203125, 14.337158203125
k, aN, sum = 11, 0.889892578125, 15.22705078125
k, aN, sum = 12, 0.73828125, 15.96533203125
k, aN, sum = 13, 0.573486328125, 16.538818359375
k, aN, sum = 14, 0.3955078125, 16.934326171875
k, aN, sum = 15, 0.204345703125, 17.138671875</span>那么这个面积到底是多大呢?
<span style="font-size:18px;">>>>
面积为: 17.999996499501062
def tmp():
sum_ = 0;
x0 = 0;
dx = 0.001;
while x0 <= 3:
y0 = 9-math.pow(x0, 2);
y1 = 9-math.pow(x0+dx, 2);
sum_ += (y0+y1)/2*dx;
x0+=dx;
print('面积为:', sum_);</span>应该是18
9x-1/3x^3 | [0, 3] = 18
这个九连环,阿伟小时候一直很想玩,可惜一直没能如愿,
现在看来,不光这游戏难玩得要命,光这解答就这么的难懂。
<span style="font-size:18px;">>>>
0
1
2
5.0
10.0
21.0
42.0
85.0
170.0
341.0
#九连环
def nineRing(N = 9):
if N == 0:
return 0;
elif N == 1:
return 1;
elif N == 2:
return 2;
else:
return math.pow(2, N-1)+nineRing(N-2);
def tmp():
for i in range(10):</span>
<span style="font-size:18px;">>>>
0
1
2
5.0
10.0
21.0
42.0
85.0
170.0
341.0
682.0
1365.0
2730.0
5461.0
10922.0
21845.0
43690.0
87381.0
174762.0
349525.0</span>
[人叫板老师]虽然已经够与时俱进了,但很明显在这件事情上还是远远落后了,
1500元,后面再加个0,差不多能买一平米,还不能挑地方。
所以这个题,小伟连算的兴趣都没有了。
本节到此结束,欲知后事如何,请看下回分解。






































 1554
1554

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








