文章目录
一、主要内容
问题的提出
- 同一个逻辑函数可以有多种表达形式;
- 一种形式的表达式,对应一种电路;
- 表达形式越复杂,则电路越复杂;
如何处理函数,以实现用尽量少的单元电路、尽量简单的电路类型来达到目的。即,逻辑函数要化简。
函数化简的目的
- 逻辑电路所用门的数量少,每个门的输入端个数少,降低成本;
- 逻辑电路构成级数少,保证逻辑电路能可靠地工作,提高电路的工作速度和可靠性。
函数化简的方法:
- 代数化简法(公式法)
- 卡诺图化简法
二、代数法化简逻辑函数
代数法化简逻辑函数的实质是反复运用逻辑代数的公式和规则,消去表达式中的多余项和多余变量。在用代数法化简逻辑函数时, 往往要依靠经验和技巧 ,带有一定的试凑性。
方法:
- 并项: 利用 A B + A B ‾ = A AB + A \overline B = A AB+AB=A 将两项并为一项,且消去一个变量 B B B;
- 消项: 利用 A + A B = A A + AB = A A+AB=A 消去多余的项 A B AB AB;
- 消元:利用 A + A ‾ B = A + B A + \overline AB = A + B A+AB=A+B 消去多余变量 A ‾ \overline A A;
- 配项:利用 A B + A ‾ C + B C = A B + A ‾ C AB + \overline AC + BC = AB + \overline AC AB+AC+BC=AB+AC 和互补律、重叠律先增添项,再消去多余项。
函数表达式一般化简成 与-或式 ,其最简应满足的两个条件:
1)表达式中“与”项的个数最少;
2)在满足1)的前提下,每个“与”项中的变量个数最少。
e . g . e.g. e.g. 化简 F = A C ‾ + A B C + A C D ‾ + C D F = A\overline C + ABC + AC\overline D + CD F=AC+ABC+ACD+CD。
F = A C ‾ + A B C + A C D ‾ + C D = A ( C ‾ + B C ) + C ( A D ‾ + D ) = A ( C ‾ + B ) + C ( A + D ) = A C ‾ + A B + A C + C D = A ( C ‾ + C ) + A B + C D = A ( 1 + B ) + C D = A + C D \begin{aligned} F &= A\overline C + ABC + AC\overline D + CD \\ &= A(\overline C + BC) + C(A\overline D + D)\\ &= A(\overline C + B) + C(A+D)\\ &= A\overline C + AB + AC + CD\\ &= A(\overline C + C) + AB + CD\\ &= A(1 + B) + CD = A +CD \end{aligned} F=AC+ABC+ACD+CD=A(C+BC)+C(AD+D)=A(C+B)+C(A+D)=AC+AB+AC+CD=A(C+C)+AB+CD=A(1+B)+CD=A+CD
实际上,我们最经常使用的是卡诺圈法,代数法化简常常作为结果的印证,我也就不麻烦的输入公式了,直接截图吧。


三、卡诺图法化简逻辑函数
1. 卡诺图
卡诺图:是真值表的图形表示:
- 将变量分成两组,构成二维表;
- 行列组合排列顺序为循环码;
- 表中每个方格对应真值表中的一行,代表一个最小项。

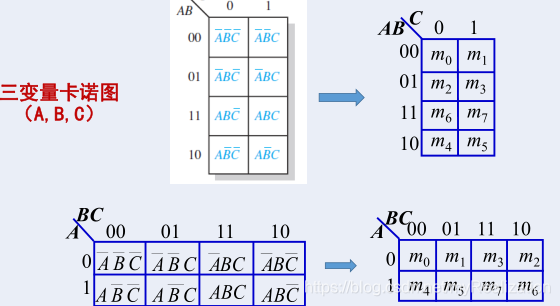

 ■ \blacksquare ■ 逻辑相邻性
■ \blacksquare ■ 逻辑相邻性
- 相邻方格的最小项,具有 逻辑相邻性 ,即有一个变量互为反变量;
- 具有逻辑相邻性的方格有
• 相接 —— 几何位置相邻的方格
• 相对 —— 上下两边、左右两边的方格
• 相重 —— 多变量卡诺图,以对称轴相折叠,叠在一起的方格(五变量)


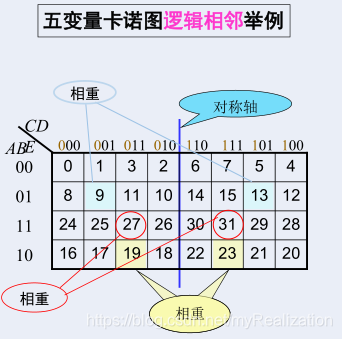
2. 卡诺图填图
卡诺图有什么用?为什么要用循环码?
- 循环码:相邻两个码字有一位相反;
- 卡诺图:逻辑相邻项有一个变量互为反变量;
- 卡诺图中的两个逻辑相邻项相加可以消去一个变量。
用卡诺图法对逻辑函数进行化简时,首先要确定函数与卡诺图的关系,将函数用卡诺图的形式表现出来。真值表、表达式、卡诺图都可以表达一个逻辑函数。
1. 真值表填卡诺图
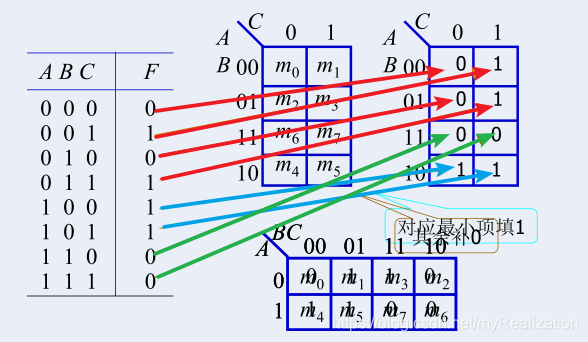
2. 表达式化为最小项表达式填卡诺图
对于 F = A ‾ B C ‾ + A B D + A C F = \overline AB\overline C + ABD + AC F=








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 5456
5456

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










