【算法学习】字符串专题 Manacher算法

最新推荐文章于 2021-05-17 23:20:06 发布

memcpy0

最新推荐文章于 2021-05-17 23:20:06 发布

阅读量424

点赞数 2

分类专栏：数据结构和算法学习字符串 # Manacher

本文链接：https://blog.csdn.net/myRealization/article/details/107848059

版权

字符串同时被 3 个专栏收录

110 篇文章 3 订阅

订阅专栏

数据结构和算法学习

89 篇文章 41 订阅

订阅专栏

Manacher

2 篇文章 0 订阅

订阅专栏

文章目录

1. 题目：求字符串中最长回文子串的长度
2. 进阶：末尾添加字符串形成回文子串
3. Manacher算法介绍
4. 其他题目

1. 题目：求字符串中最长回文子串的长度

给出一个字符串 str ，返回 str 中最长回文子串的长度。

如 str="123" ，最长的回文子串是 "1", "2", "3" ，所以返回 1 。或者 str="abc1234321ab" ，其中的最长回文子串是 "1234321" ，所以返回 7 。

2. 进阶：末尾添加字符串形成回文子串

拓展：给定一个字符串 str ，通过添加字符的方式使得 str 整体都变为回文子串，只能够在 str 的末尾添加字符，请返回 str 后面添加的最短字符串。

如：str="12" ，在末尾添加 "1" 后，变为 "121" ，是回文串，而且是最短的，因此返回 "1" ；添加 "21" 也会变成回文串 "1221" ，但不是最短。

要求：如果 str 的长度为 N ，解决原问题和进阶问题的时间复杂度都是 $\text{O(N)}$ 。

3. Manacher算法介绍

马拉车算法解决的问题是：在线性时间内找到一个字符串的最长回文子串。它的优势在于：比较好理解和实现。

(1) 中心扩展法

一个好理解的方法是：从左到右遍历字符串，遍历到每个字符的时候，都看看以这个字符为中心，能够产生多大的回文字符串。

如字符串 abacaba ，以 str[0]='a' 为中心的回文子串最大长度是 1 ；以 str[1]='b' 为中心的回文子串最大长度是 3 …… 其中，最大的回文子串是以 str[3]='c' 为中心的 abacaba ，长度为 7 。

这种方法很容易理解，只要解决奇数回文和偶数回文寻找方式的不同即可：

"121" 是奇回文，轴明确为 '2' 。
"1221" 是偶回文，没有确定的轴，虚轴在 "22" 之间。

而且，这种方法还有极大的优化空间：之前遍历得到的回文信息，在后面遍历的过程中完全没有使用到！每个字符都从自己的位置出发，向左右两个方向扩展检查，它们往外扩的代价都是一个级别的。以 "aaaaaaaaaa" 为例，每个 "a" 都扩展到边界才停止，于是总的时间复杂度为 $\text{O(N}^2)$ 。

(2) Manacher原理

Manacher算法在中心扩展法的基础上进行了改进：之前字符的扩展过程，可以指导后面字符的扩展过程，避免了从头开始，做到了 $\text{O(N)}$ 的时间复杂度。

下面将详细介绍Manacher算法的过程：

奇回文和偶回文的区分太麻烦了，所以对 str 进行预处理，把每个字符开头、结尾、中间都插入特殊字符 '#' ，得到新的字符串数组，如 str="bcbaa" 处理后得到 #b#c#b#a#a# 。这样奇回文和偶回文都统一为奇回文，都可以通过统一的扩展过程找到最大回文：
- 当然，奇回文不用处理也可以实现扩的过程，比如 "bcb" ，从 'c' 开始向左右扩展就可以找到最大回文。处理后为 "#b#c#b#" ，从 'c' 左右扩出去也可以找到最大回文；
- 对于偶回文，不处理而直接扩是找不到的，如 "aa" ，没有明确的轴，无论从哪个 'a' 出发都找不到最大回文；但是处理后变为 "#a#a#" ，可以从中间的 '#' 扩展出去，找到最大回文。
- 需要注意的是，这个特殊字符是什么都无所谓，甚至可以是字符串中出现的字符，这不会影响最终的结果。
```
public char[] ManacherString(String str) {
	char[] charArr = str.toCharArray();
	char[] res = new char[str.length() * 2 + 1];
	int index = 0;
	for (int i = 0; i != res.length; ++i) {
		res[i] = (i & 1) == 0 ? '#' : charArr[index++];
	}
	return res;
}
```

str 处理之后的字符串为 charArr 。每个字符（包括特殊字符）都进行优化后的扩展过程。先解释下面三个辅助变量的意义：
- 数组 pArr ，长度和 charArr 一样，它的意义是：以 i 位置上的字符 charArr[i] 作为回文中心的情况下，扩展出去得到的最大回文半径是多少。
  
  以 "#c#a#b#a#c#" 来说，pArr 为 [1,2,1,2,1,6,1,2,1,2,1] 。我们的整个过程就是在从左到右遍历的过程中，依次计算每个位置的最大回文半径值。
- 整数 pR ，它的意义是：之前遍历的所有字符的所有回文半径之中，最右即将到达的位置。以 "#c#a#b#a#c#" 来说，还没有遍历之前的 pR ，初始设置为 -1 ：
  - charArr[0]='#' 的回文半径为 1 ，所以目前回文半径向右只能扩展到位置 0 ，最右即将到达的位置变为 1(pR = 1) ；
  - charArr[1]='c' 的回文半径为 2 ，所有回文半径向右只能扩展到位置 2 ，最右即将到达的位置变为 3(pR = 3) ；
  - charArr[2]='#' 的回文半径为 1 ，所以目前回文半径向右只能扩展到位置 2 ，最右即将到达的位置不变；
  - charArr[3]='a' 的回文半径为 2 ，所以位置 3 向右能够扩展到位置 4 ，回文半径最右即将到达的位置变为 5(pR = 5) 。
  - charArr[4]='#' 的回文半径为 1 ，所以位置 4 向右只能扩到位置 4 ，回文半径最右即将到达的位置不变；
  - charArr[5]='b' 的回文半径为 6 ，所以位置 5 向右能够扩展到位置 10 ，回文半径最右即将到达的位置变为 11(pR = 11) 。
  - 此时，已经到达整个字符数组的结尾，所以之后 pR 不再改变。即 pR 就是遍历过的所有字符中向右扩展出来的最大右边界。只要右边界更往右，就更新。
- 整数 index ，表示最近一次 pR 更新时，那个回文中心的位置。以刚刚的例子来说，遍历到 charArr[0] 时 pR 更新，index = 0 ；遍历到 charArr[1] 时 pR 更新，index 更新为 1 ……遍历到 charArr[5] 时 pR 更新，index 更新为 5 。之后的过程中，pR 不再更新，所以 index 将一直是 5 。

只要能从左到右依次计算出数组 pArr 每个位置的值，最大的那个值就是处理后的 charArr 中最大的回文半径，对应原来的字符串，问题就解决了。以下步骤就是从左到右依次计算 pArr 数组中每个位置的值的过程。
- 现在计算位置 i 的字符 charArr[i] 。之前位置的计算过程中，pR, index 的值不断在更新，i 之前的回文中心 index 扩展出了一个目前最右的回文边界 pR 。
- 如果 pR - 1 位置没有包裹着当前的 i 位置。还是 "#c#a#b#a#c#" 这个例子，计算到 charArr[1]='c' 时，pR 为 1 ，即右边界在位置 1 ，是最右回文半径即将到达但没有到达的位置，所以当前的 pR - 1 位置没有包住当前的 i 位置。此时和普通的中心扩展法一样！从 i 位置字符开始向左右两侧扩展出去检查，这一过程没有获得优化。
- 如果 pR - 1 位置包裹着当前的 i 位置。计算到 charArr[6...10] 时，pR 都为 11 ，此时 pR - 1 包括了位置 6~10 ，检查过程可以获得优化！这也是 $\text{Manacher}$ 算法的核心：
  
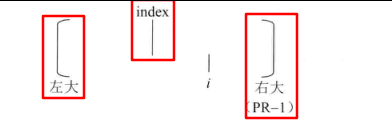
  上图中， i 位置是计算当前位置最大回文半径 pArr[i] 的位置，pR - 1 包括位置 i 。根据 index 的定义，index 是 pR 更新时那个回文中心的位置，所以如果 pR - 1 位置以 index 为中心对称，即左大位置。从左大位置到 pR - 1 右大位置一定是以 index 为中心的回文串，被称作大回文串。
  
  既然最大回文半径数组 pArr 从左到右计算，所以位置 i 之前的所有位置都已经计算过回文半径。假设 i 位置以 index 为中心向左对称的位置为 i' ，则 i' 的回文半径也已经计算过。以 i' 为中心的最大回文串大小 pArr[i'] 必然只有三种情况，其左边界和右边界分别记为左小和右小：
  - 左小和右小完全在左大和右大内部，即以 i' 为中心的最大回文串完全在以 index 为中心的最大回文串内部：
    
    a' 是左小位置的前一个字符，b' 是右小位置的后一个字符；a 是 a' 以 index 为中心的对称字符，b 是 b' 以 index 为中心的对称字符。此时不难发现，以位置 i 为中心的最大回文串可以直接确定，就是 右小’到左小’ 这一段。
    
    原因在于：左小到右小 这一段以 index 为中心，对称过去就是 右小’到左小’ 这一段，后者完全是前者 左小到右小 的逆序。同时，左小到右小 这一段是以 i' 为回文中心的回文串，所以 右小’到左小’ 这一段也一定是回文串。
    
    从而，以位置 i 为中心的最大回文串起码是 右小’到左小’ 这一段，而 a' != b' ，那么对应的 a != b ，说明以位置 i 为中心的最大回文串就是 右小’到左小’ 这一段，不会扩得更大。
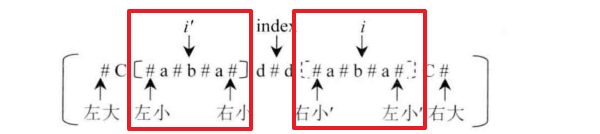
  - 左小和右小的左侧部分在左大和右大的外部，如下图：
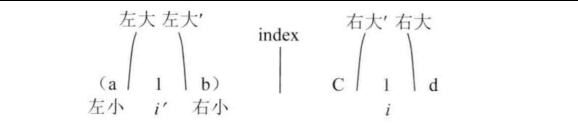
    上图中，a 是左大位置的前一个字符，d 是右大位置的后一个字符，左大’ 是左大以位置 i' 为中心的对称位置，右大’ 是右大以位置 i 为中心的对称位置。b 是 左大’ 位置的后一个字符，c 是 右大’ 位置的前一个字符。
    
    处于这种情况下，以位置 i 为中心的最大回文串可以直接确定，就是 右大到右大’ 这一段。
    
    原因在于：首先，左大到左大’ 这一段和 右大’到右大 这一段是关于 index 对称的，所以后者是前者 左大到左大’ 的逆序；
    
    同时，左小到右小 这一段是以 i' 位置为中心的回文串，那么 左大到左大’ 也是回文串，它的逆序——右大’到右大 也一定是回文串。也就是说，以位置 i 为中心的最大回文串起码是 右大’到右大 这一段；
    
    左小到右小 这一段是回文串，说明 a == b ，b 和 c 关于 index 对称，说明 b == c 。但是 左大到右大 这一段没有扩得更大，说明 a != d ，则 d != c 。从而以位置 i 为中心的最大回文串就是 右大’到右大 这一段。
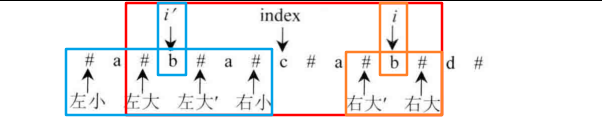
  - 左小和左大是同一个位置，以 i' 为中心的最大回文串压在以 index 为中心的最大回文串的边界上，如下图：
    
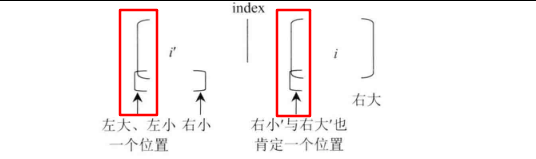
    图中，左大和左小的位置重叠，右小’ 是右小位置以 index 为中心的对称位置，右大’ 是右大位置以 i 为中心的对称位置。易知，右小’和右大’ 的位置重叠。
    
    此时，以位置 i 为中心的最大回文子串起码是 右大’到右大 这一段，但可能扩得更大。因为这一段是 左小到右小 这一段以 index 为中心对称过去的，两端互为逆序；同时 左小到右小 是回文串，所以 右大’到右大 这一段也肯定是回文串。
    
    但是，以位置 i 为中心的最大回文串可能扩得更大，如下图：
    
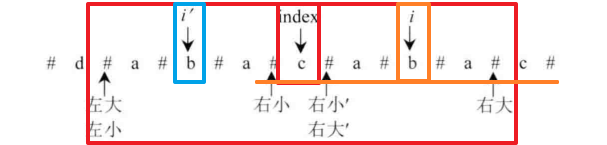
    说明，在这一情况下，扩出去的过程可以得到优化，但还是需要进行扩出去的检查。
按照步骤3的逻辑从左到右计算出 pArr 数组后，再遍历一次 pArr 数组，找出最大的回文半径。如果 i 的回文半径最大，即 pArr[i] = max 。但是 max 只是 charArr 的最大回文半径，对应回原来的字符串，求出最大回文子串的长度为 max - 1 。比如原串为 "121" ，处理成 charArr 之后为 "#1#2#1#" 。在其中，位置 3 的回文半径最大为 pArr[3] = 4 ，对应回原字符串的最大回文子串长度为 4 - 1 = 3 。

(3) 算法时间复杂度

$\text{Manacher}$ 的时间复杂度为 $\text{O(N)}$ ，它在扩出去检查这一步上做了相当明显的优化。

原字符串处理后变为 $\text{2N}$ 长度。从步骤3来看，要么在计算一个位置的回文半径时完全不需要扩出去检查(情况1和情况2)，要么每次扩充出去检查都会导致 pR 变量的更新(情况3)，让回文半径到达更右的位置。

pR 从 -1 增加到 2N ，而且从不减小，所以扩出去检查的次数就是 $\text{O(N)}$ 的级别。 $\text{Manacher}$ 算法的时间复杂度是 $\text{O(N)}$ 。

public int maxLcpsLength(String str) {
	if (str == null || str.length() == 0) return 0;
	char[] charArr = manacherString(str);
	int[] pArr = new int[char.length];
	int index = -1, pR = -1;
	int max = Integer.MIN_VALUE;
	for (int i = 0; i != charArr.length; ++i) {
		//i<=pR-1表示包括住,对称位置的i'为index-(i-index)
		//情况1不用比较,记为对称位置的i'的最大回文半径
		//情况2不用比较,记为pR - i
		//情况3需要从i'的最大回文半径开始向左右比较
		//没有包括住,此时以i为中心的最大回文半径开始为1
		pArr[i] = pR > i ? Math.min(pArr[2 * index - i], pR - i) : 1;
		//向左右扩展,增加最大回文半径
		while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
			if (charArr[i + pArr[i]] == charArr[i - pArr[i]])
				pArr[i]++;
			else break;
		}
		//i + pArr[i] > pR
		if (i + pArr[i] > pR) {
			pR = i + pArr[i]; //更新最右即将到达的位置
			index = i;		  //更新回文中心
		}  //pArr[i]是以i为中心的最大回文半径
		max = Math.max(max, pArr[i]); //寻找最大的回文半径
	}
	return max - 1;
}

(4) 进阶题目解法

这一题的实质是查找在必须包含最后一个字符的情况下，最长的回文子串是什么。把之前不是最长回文子串的部分逆序过来，就是应该添加的部分。

如 "abcd123321" ，必须包含最后一个字符的情况下，最长回文子串是 "123321" ，之前不是最长回文子串的部分是 "abcd" ，把它逆序过来 "dcba" 添加到末尾即可。

修改 $\text{Manacher}$ 算法：从左到右计算回文半径时，关注回文半径最右即将到达的位置 pR ，一旦发现已经到达最后 pR == charArr.length ，说明必须包含最后一个字符的最长回文子串半径已经找到，直接退出检查过程，返回该添加的字符串即可。

代码：

public String shortestEnd(String str) {
	if (str == null || str.length() == 0) return null;
	char[] charArr = manacherString(str);
	int[] pArr = new int[charArr.length];
	int index = -1;
	int pR = -1;
	int maxContainsEnd = -1;
	for (int i = 0; i != charArr.length; ++i) {
		pArr[i] = pR > i ? Math.min(pArr[2 * index - i], pR - i) : 1;
		while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
			if (charArr[i + pArr[i]] == charArr[i - pArr[i]]) 
				++pArr[i];
			else break;
		}
		if (i + pArr[i] > pR) {
			pR = i + pArr[i];
			index = i;
		}
		if (pR == charArr.length) {
			maxContainsEnd = pArr[i];
			break;
		}
	}
	char[] res = new char[str.length() - maxContainsEnd + 1];
	for (int i = 0; i < res.length; ++i)  
		res[res.length - 1 - i] = charArr[i * 2 + 1];
	return String.valueOf(res);
}

4. 其他题目

洛谷 P3805 manacher算法：求出最长的回文串长度。
LeetCode 5. Longest Palindromic Substring：求出最长回文串长度。
LeetCode 214. Shortest Palindrome：在 str 之前添加字符将其转换为回文串，返回可以用这种方式转换的最短回文串，不是返回 str 前面添加的最短字符串。是本节进阶题目的一个小扩展。

memcpy0

关注

2
点赞
踩
4

收藏

觉得还不错? 一键收藏
打赏
0
评论
【算法学习】字符串专题 Manacher算法

文章目录1. 题目：求字符串中最长回文子串的长度2. 进阶：添加字符串形成回文子串3. Manacher算法介绍(1) 中心扩展法(2) Manacher原理(3) 算法时间复杂度(4) 进阶题目解法4. 其他题目1. 题目：求字符串中最长回文子串的长度给出一个字符串 str ，返回 str 中最长回文子串的长度。如 str="123" ，最长的回文子串是 "1", "2", "3" ，所以返回 1 。str="abc1234321ab" ，其中的最长回文子串是 "1234321" ，所以返回 7
复制链接

扫一扫