算法学习笔记() 数论之素数判断和计数——埃式筛、欧拉筛、区间素数、素因子分解、欧拉与Mobius函数

本文属于「算法学习」系列文章的汇总目录。之前的「数据结构和算法设计」系列着重于基础的数据结构和算法设计课程的学习，与之不同的是，这一系列主要用来记录大学课程范围之外的高级算法学习、优化与应用的全过程，同时也将归纳总结出简洁明了的算法模板，以便记忆和运用。在本系列学习文章中，为了透彻理解算法和代码，本人参考了诸多博客、教程、文档、书籍等资料，由于精力有限，恕不能一一列出，这里只列示重要资料的不完全参考列表：

• 算法竞赛进阶指南，李煜东，河南电子音像出版社，GitHub Tedukuri社区以及个人题解文章汇总目录

为了方便在PC上运行调试、分享代码，我还建立了相关的仓库。在这一仓库中，你可以看到算法文章、模板代码、应用题目等等。由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏算法学习系列文章目录一文以作备忘。

---

素数的定义和性质见【数论】第1章 整数的可除性(1) 整除概念与带余除法(2) 素数。本文中我们将讨论，如何用算法求解两个关于素数的问题——素性测试和素数计数（筛法）。

1. 素性测试

问题很简单：输入一个很大的正整数 $n$ ，判断它是不是素数。

1.1 用试除法判断素数

根据素数的定义（定义1.1.2），一个数 $n$ ，如果不能被 $[2,n-1]$ 内的所有整数整除，$n$ 就是素数。当然，我们不需要把 $[2,n-1]$ 内的数都试一遍，这个范围可以缩小到 $[2,\sqrt{n}]$ 。

即给定 $n$ ，如果它不能被 $[2,\sqrt{n}]$ 内的所有数整除，它就是素数（证明见定理1.1.1）。因此，我们只要检查 $[2,\sqrt{n}]$ 内的数，如果 $n$ 不是素数，就一定能找到一个数 $a(2\le a\le \sqrt{n})$ 整除 $n$ ；如果不存在这样的 $a$ ，那么 $[\sqrt{n},n-1]$ 中也不存在 $b(\sqrt{n}\le b<n)$ 整除 $n$ 。

后面的讲解中，会进一步缩小以上判断的范围：$[2,\sqrt{n}]$ 内所有的素数。原理很简单——如果 $n$ 是合数，则 $n$ 一定能被 $[2,\sqrt{n}]$ 内的某个数 $y$ 整除：

• $y$ 是素数时，就不讨论了；
• $y$ 是合数时，则 $y$ 一定能被 $[2,\sqrt{y}]$ 内的某个数整除，如此递归，最终必然对应到一个比它小的素数 $x$ 、能被 $x$ 整除。

用试除法判断素数，复杂度是 $O(\sqrt{n})$ ，对于 $n\le 10^{12}$ 的数是没有问题的。下面是试除法判断素数的模板代码：

bool isPrime(int n) {
	if (n <= 1) return false;	// 1不是素数
	if (n == 2) return true;	// 2是素数
	if (n % 2 == 0) return false; // 除2以外的正偶数都不是素数
	int sqr = sqrt(n);
	for (int i = 2; i <= sqr; ++i) // 也可以写成 for(int i = 2; i * i <= n; ++i)
		if (n % i == 0) return false; // 能整除,不是素数
	return true;
}

1.2 巨大素数的判断——Miller-Rabin 测试

如果 $n$ 非常大，例如POJ 1811题 $1\le n<2^{54}$ ，判断 $n$ 是不是素数。如果用试除法，$\sqrt{n}=2^{27}\approx 10^8$ ，复杂度仍然太高。此时需要用到特殊而复杂的方法，见 《ACM/ICPC算法训练教程》P127页 余立功 清华大学出版社。

要测试 $n$ 是否为素数，首先将 $n-1$ 分解为 $2^{s}d$ 。每次测试开始时，随机选一个 $[1,n-1]$ 的整数 $a$ ，如果对所有的 $r\in [0,s-1]$ ，都满足 $a^d\mathrm{m}\mathrm{o}\mathrm{d}n\ne 1$ 且 $a^{2^{r}d}\mathrm{m}\mathrm{o}\mathrm{d}n\ne -1$ ，则 $n$ 是合数。否则，$n$ 有 $\frac{3}{4}$ 的记录为素数。为了提高测试的正确性，可选择不同的 $a$ 进行多次测试。

Miller-Rabin 素性测试的模板代码如下：

bool test(int n, int a, int d) {
	if (n == 2) return true; // 2是素数
	if (n == a) return true; // 选择的a也是素数
	if ((n & 1) == 0) return false; // 非2的偶数不是素数
	while (!(d & 1)) d = d >> 1;
	int t = fastPow(a, d, n); // 快速幂,计算a^d % n
	while ((d != n - 1) && (t != 1) && (t != n - 1)) {
		t = (long long)t * t % n;
		d = d << 1;
	}
	return (t == n - 1 || (d & 1) == 1);
}

bool isPrime(int n) { // false表示n为合数,true表示n有很大几率为素数
	if (n < 2) return false;
	int a[] = {2, 3, 61}; // 测试集,更大的测试范围需要更大的测试集
	for (int i = 0; i <= 2; ++i)
		if (!test(n, a[i], n - 1)) return false;
	return true;
}

算法的时间复杂度为 $O(\log n)$ 。

---

2. 素数筛法与计数

一个与素数相关的问题是求 $[2,n]$ 内所有的素数。如果用上面的试除法，一个个单独判断，太慢了。

2.1 埃利特斯拉筛法

埃式筛法是一种古老而有效的方法，可以快速找到 $[2,n]$ 内所有的素。对于初始队列 { 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , … , n } \{ 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, \dots, n\} {2,3,4,5,6,7,8,9,10,11,12,13,…,n} ，操作步骤如下：
（1）输出最小的素数 $2$ ，然后筛掉 $2$ 的倍数，剩下 { 3 , 5 , 7 , 9 , 11 , 13 , …   } \{ 3, 5, 7, 9, 11, 13, \dots \} {3,5,7,9,11,13,…} ；
（2）输出最小的素数 $3$ ，然后筛掉 $3$ 的倍数，剩下 { 5 , 7 , 11 , 13 , …   } \{ 5, 7, 11, 13, \dots \} {5,7,11,13,…} ；
（3）输出最小的素数 $5$ ，然后筛掉 $5$ 的倍数，剩下 { 7 , 11 , 13 , …   } \{ 7, 11, 13, \dots \} {7,11,13,…}
（4）继续以上步骤，直到队列为空。

下面是朴素的埃式筛法模板代码。其中 inp[i]（is not prime）记录数 $i$ 的状态，如果 inp[i] = true ，表示它被筛掉了、不是素数。用 primes 数组存放素数，例如 prime[0] 是第一个素数 $2$ 。

const int maxn = 1e7; 				// 定义空间大小,1e7约1.25MB
vector<int> primes;					// 存放素数
bitset<maxn> inp;					// inp[i]=true,表示i不是素数
int E_sieve(int n) {				// 埃式筛法,计算[2,n]内的素数
	for (int i = 2; i <= n; ++i) {	// 从第1个素数2开始,可优化(1)
		if (inp[i] == false) { 		// i是素数
			primes.push_back(i); 	// 保存到primes中
			for (int j = i * 2; j <= n; j += i) // i的倍数都不是素数,可优化(2)
				inp[j] = true;
		}
	}
	return primes.size();			// 统计素数的个数
}

时间复杂度：$2$ 的倍数被筛掉，计算 $n/2$ 次；$3$ 的倍数被筛掉，计算 $n/3$ 次；$5$ 的倍数被筛掉，计算 $n/5$ 次。依次类推，总次数是 $O(n/2+n/3+n/5+\dots )$ ，这里直接给出结果，即 $O(n\log {\log }_{2}n)$ 。
空间复杂度：程序用到了位图 bitset<maxn> inp ，当范围达到 $10^7$ 时约为1.25MB，再加上 primes ，空间不会超过10MB。一般题目会限制空间为65MB。

上述代码有两处可以优化：

• 用来做筛除的数为 $2,3,5$ 等，最多到 $\sqrt{n}$ 就可以了，其原理和试除法一样——合数 $k(\le n)$ 必定可以被一个小于等于 $\sqrt{k}(\le \sqrt{n})$ 的素数整除（见埃利特斯拉筛法的相关说明）。例如，求 $n=100$ 以内的素数，用 $2,3,5,7$ 筛就足够了。注意，此时如果要存储素数，还需要一次额外的for循环。
• for (int j = i * 2; j <= n; j += i) 中的 j = 2 * i ，可优化为 j = i * i ，减少重复筛数，注意当 $n\ge 10^6$ 时，i * i 可能溢出，需要强制类型转换。例如 $i=5$ 时，$2\times 5,3\times 5,4\times 5$ 早已在前面 $i=2,3,4$ 的时候筛过了。

优化后的埃式筛法模板代码如下：

const int maxn = 1e7; 				// 定义空间大小,1e7约1.25MB
vector<int> primes;					// 存放素数
bitset<maxn> inp;					// inp[i]=true,表示i不是素数
int E_sieve(int n) {				// 埃式筛法,计算[2,n]内的素数
	int sqr = sqrt(n);
	for (int i = 2; i <= sqr; ++i)  // 从第1个素数2开始,可写成i*i<=n
		if (inp[i] == false)  		// i是素数
			for (int j = i * i; j <= n; j += i)
				inp[j] = true;
	for (int i = 2; i <= n; ++i)
		if (inp[i] == false)
			primes.push_back(i); 	// 保存到primes中
	return primes.size();			// 统计素数的个数
}

埃式筛法还不错，但还是做了一些无用功，某些合数会被筛几次，比如 $12$ 会被 $2$ 和 $3$ 筛两次。不过，埃式筛法可以近似地看做 $O(n)$ 的，一般也够用了。只是在一些数据范围达到 1e7 的题目中，难以让人满意，下面就介绍欧拉筛法，时间复杂度仅为 $O(n)$ 的线性筛法。

2.2 欧拉筛法

如何确保每个合数只被筛选一次呢？我们只要用它的最小质因子来筛选即可，显然，每个数的最小质因子只有一个、只能被筛一次。这就是欧拉筛——在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复筛数的目的。

我们直接看欧拉筛的模板代码：

const int maxn = 1e7; 				// 定义空间大小,1e7约1.25MB
vector<int> primes;					// 存放素数
bitset<maxn> inp;					// inp[i]=true,表示i不是素数
int Euler_sieve(int n) {			// 欧拉筛法,计算[2,n]内的素数
	for (int i = 2; i <= n; ++i) {  // 从第1个素数2开始
		if (inp[i] == false)
			primes.push_back(i); 	// 保存到primes中
		for (int j = 1; j < primes.size(); ++j) {
			if (i * primes[j] <= n) break; // 超出要求的范围,退出
			inp[i * primes[j]] = true;	   // 解释
			if (i % primes[j] == 0) break; // 解释
		}
	}
	return primes.size();			// 统计素数的个数
}

特别地，对于 inp[i * primes[j]] = true 的解释：这里不是用 i 的倍数消去合数，而是用 primes 里面记录的素数，从小到大来当做消去合数的最小质因子。打表观察来理解，可见是用最小质因子 primes[j] 的 i 倍数来筛去合数，且筛去的合数没有重复：

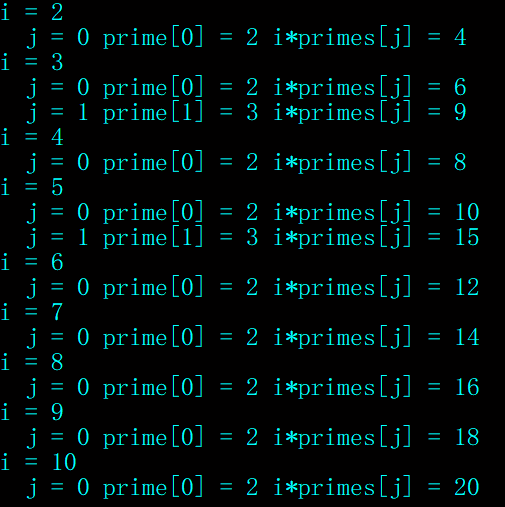
对于 i % primes[j] == 0 就跳出循环的解释——这是避免重复筛数的关键所在，此时显然有 primes[i] | i ，即有 i = primes[j] * q ，如果继续循环到 j + 1 ，i * primes[j + 1] = primes[j] * q * primes[j + 1] ，注意到这里的 primes[j] 才是最小质因子，应该由 primes[j] 在 i = q * primes[j + 1] 时筛去，而不是由 primes[j + 1] 在 i = primes[j] * q 时筛去，所以要跳出循环。

举例说明，当 i = 8, j = 1, primes[j] = 2 时，如果不跳出循环，prime[j + 1] = 3, 8 * 3 = 24 = (2 * 4) * 3 = 2 * (4 * 3) ，会筛去 24 ——实际上，24 应在 i = 12 时筛去、而不是在 i = 8 时筛去。

2.3 筛法应用于小区间大素数筛选

用埃式/欧拉筛法求 $[2,n]$ 内的素数，能解决 $n\le 10^7$ 的问题。如果 $n$ 更大，某些情况下还是可以用筛法来处理，这就是小区间大素数的计算（小的区间、大的素数）——把 $[2,n]$ 看做一个区间，然后把筛法扩展到求区间 $[a,b]$ 的素数，$a<b\le 10^{12},b-a\le 10^6$ 。

前文提到，用试除法判断 $n$ 是否为素数，更深的原理为：如果它不能被 $[2,\sqrt{n}]$ 内的所有素数整除，它就是素数。容易理解这个原理：$[2,\sqrt{n}]$ 内的非素数 $y$ ，肯定对应一个比它小的素数 $x$ 。在用试除法时，如果 $n$ 能被 $x$ 整除，则证明了 $n$ 不是素数，就不用在试 $y$ 了。

这个原理可以和筛法结合，用来解决大区间求素数的问题。具体来说，先用埃式/欧拉筛法求 $[2,\sqrt{b}]$ 内的素数，然后用这些素数来筛选 $[a,b]$ 区间的素数——对每个 $[a,b]$ 内的数，如果它是合数，则必定被 $[2,\sqrt{b}]$ 内的某个素数整除。
（1）时间复杂度：使用埃式筛法，则为 $O(\sqrt{b}\log \log \sqrt{b})+O((b-a)\sqrt{b-a})$ ；使用欧拉筛法，则为 $O(\sqrt{b})+O((b-a)\sqrt{b-a})$ ？？？
（2）空间复杂度：需要定义两个数组，一个用来处理 $[2,\sqrt{b}]$ 内素数，另一个用于处理 $[a,b]$ 内的素数，空间复杂度为 $O(\sqrt{b})+O(b-a)$ 。

2.4 更大的素数——大区间素数计算

如果要统计更大范围内的素数个数，例如 $n=10^{11}$ 时有 $40$ 多亿个素数（[2, n]内素数的数量），就要用到更加复杂的数学方法。

---

3. 素因子分解

$n$ 的质因数要么是 $n$ 本身（$n$ 是质数）、要么一定小于等于 $\sqrt{n}$ 。因此可用小于等于 $\sqrt{n}$ 的数对 $n$ 进行试除，一直到不能除为止。这时候剩下的数如果不是 $1$ ，那么就是 $n$ 最大的质因数。

质因数分解的模板代码如下，时间复杂度为 $O(\sqrt{n})$ ：

vector<int> pfac; // 存储质因数
vector<int> fexp; // 存储质因数对应的指数
void factor(int n) {
	if (n <= 1) return;
	int sqr = sqrt(n), now = n;
	for (int i = 2; i <= sqr; ++i) {
		if (now % i == 0) {
			pfac.push_back(i);
			int cnt = 0;
			while (now % i == 0) {
				++cnt;
				now /= i;
			}
			fexp.push_back(cnt);
		}
	}
	if (now != 1) {
		pfac.push_back(now);
		fexp.push_back(1);
	}
}

---

4. 欧拉函数计算

计算 $n$ 的欧拉函数 $\Phi (n)$ ——其定义表示，小于等于 $n$ 的数中与 $n$ 互质的数的数目。

欧拉函数求值的方法是：
（1）$\Phi (1)=1$ ；
（2）若 $n$ 是素数 $p$ 的 $k$ 次幂，则 $\Phi (n)=p^k-p^{k-1}=(p-1)p^{k-1}$ ；
（3）若 $m,n$ 互质，则 $\Phi (mn)=\Phi (m)\Phi (n)$ 。

根据欧拉函数的定义和性质，可以推出欧拉函数的递推式：令 $p$ 为 $n$ 的最小质因数，若 $p^2\mid n$ ，则 $\Phi (n)=\Phi (\frac{n}{p})\times p$ ；否则 $\Phi (n)=\Phi (\frac{n}{p})\times (p-1)$ 。

计算欧拉函数的模板代码如下，时间复杂度为 $O(n\log n)$ ，全局变量 phi[] 中存储了 $[1,maxn]$ 中每个数的欧拉函数值：

const int maxn = 111111;
int minDiv[maxn], phi[maxn], sum[maxn];
void getPhi() {
	for (int i = 1; i < maxn; ++i) minDiv[i] = i;
	for (int i = 2; i * i < maxn; ++i) { // 埃式筛法计算每个数的最?质因子
		if (minDiv[i] == i)
			for (int j = i * i; j < maxn; j += i)
				minDiv[j] = i;
	}
	phi[1] = 1;
	for (int i = 2; i < maxn; ++i) {
		phi[i] = phi[i / minDiv[i]];
		if ((i / minDiv[i]) % minDiv[i] == 0) 
			phi[i] *= minDiv[i];
		else
			phi[i] *= minDiv[i] - 1;
	}
}

特别地，计算单个欧拉函数的值时，可以直接采用定义。

---

5. Mobius函数计算

计算 $n$ 的Mobius函数 $\mu (n)$ 。Mobius函数是做Mobius反演时的一个很重要的系数。Mobius函数的定义是：如果 $i$ 的质因数分解式内，有任意一个大于 $1$ 的指数，则 $\mu (i)=0$ ；否则，$\mu (i)$ 等于 $i$ 的质因数分解式内质数的个数 $\mathrm{m}\mathrm{o}\mathrm{d}2\times (-2)+1$ 。

Mobius函数有个很好的性质：$\sum _{d\mid n}\mu (d)=[n=1]$ ，其中 $[n=1]$ 代表 $n=1$ 的时候为 $1$ 、$n$ 不等于 $1$ 的时候为 $0$ 。由此可以递推地求出Mobius函数。

计算Mobius函数的模板代码如下，时间复杂度为 $O(n\log n)$ ，全局变量 mu[] 中存储了 $[1,n]$ 中每个数的Mobius函数值：

const int maxn = 1 << 20;
int mu[maxn];
int getMu() {
	for (int i = 1; i <= n; ++i) {
		int target = i == 1 ? 1 : 0;
		int delta = target - mu[i];
		mu[i] = delta;
		for (int j = i + i; j <= n; j += i)
			mu[j] += delta;
	}
}

计算单个Mobius函数时，可以直接采用定义。除了用埃式筛法外，还可用欧拉筛计算欧拉函数和Mobius函数。

---

6. 各大OJ经典题目

POJ 百炼3177，素数筛法
HDU 2138，素数判定
POJ 1811，大素数素性测试
HDU 1262，寻找素数对
HDU 2710，筛法求素数
洛谷 P3383 【模板】线性筛素数
HDU 3792，素数打表
POJ 1142，素因数分解
HDU 3826，分解质因子
HDU 6069，区间素数
POJ 2689，求 $[L,R]$ 内的素数，$1\le L<R\le 2147483647,R-L\le 10^6$
HDU 5901 Count Primes，求 $1\le n\le 10^{11}$ 范围内的素数个数
POJ 3090 欧拉函数计算