【算法学习笔记】van Emde Boas树

参考算法导论第20章 van Emde Boas树

在前面，我们见过了一些支持优先队列操作的数据结构，如二叉堆、红黑树、斐波那契堆。在这些数据结构中，不论是最坏情况或摊还情况，至少有一项重要操作只需 $O(\log n)$ 时间。实际上，由于这些数据结构都是基于关键字比较来做决定的，因此，（算导8.1节中）排序下界 $\Omega (n\log n)$ 说明，至少有一个操作必需 $\Omega (\log n)$ 的时间。这是为什么呢？因为如果 INSERT, EXTRACT-MIN 操作均需要 $o(\log n)$ 时间，那么可以通过先执行 $n$ 次 INSERT 操作，接着再执行 $n$ 次 EXTRACT-MIN 操作来实现 $o(n\log n)$ 时间内、对 $n$ 个关键字的排序。

然而，之前见到过，有时可以利用关键字包含的附加信息、来完成 $o(n\log n)$ 时间内的排序。特别地，对于计数排序，每个关键字都是介于 $0\sim k$ 之间的整数，这样排序 $n$ 个关键字、能在 $\Theta (n+k)$ 时间内完成，而当 $k=O(n)$ 时，排序时间为 $\Theta (n)$ 。由于当关键字是有界范围内的整数时，能够规避排序的 $\Omega (n\log n)$ 下界的限制，那么在类似的场景下我们应弄清楚，在 $o(\log n)$ 时间内、是否可以完成优先队列的每个操作。在这里我们将看到：van Emde Boas 树支持优先队列操作以及一些其他操作，每个操作最坏情况运行时间为 $O(\log \log n)$ 。而这种数据结构限制关键字必须为 $0\sim n-1$ 的整数且无重复。

明确地讲，van Emde Boas 树支持在动态集合上运行时间为 $O(\log \log n)$ 的操作：SEARCH, INSERT, DELETE, MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR 。这里只关注关键字的存储、而不讨论卫星数据。因为我们专注于关键字、且不允许存储重复的关键字，所以我们将实现更简单的 MEMBER(S, x) 操作，而不是去描述稍复杂的 SEARCH 操作，该 MEMBER 操作通过返回一个布尔值来指示 $x$ 是否在动态集合 $S$ 内。

到目前为止，参数 $n$ 有两个不同的用法：一个为动态集合中元素的个数，另一个为元素的可能取值范围。为避免混淆，下面用 $n$ 表示集合中当前元素的个数，用 $u$ 表示元素的可能取值范围，这样每个 van Emde Boas 树操作在 $O(\log \log u)$ 时间内运行完。要存储的关键字值的全域 universe 集合为 { 0 , 1 , 2 , … , u − 1 } \{ 0, 1, 2, \dots, u - 1\} {0,1,2,…,u−1} ，$u$ 为全域的大小。这里始终假定 $u$ 恰好为 $2$ 的幂，即 $u=2^k(k\in \mathbb{N},k\ge 1)$ 。

• （算导20.1节）开始讨论一些简单的方法，为后续内容的学习做铺垫。
• （算导20.2节）逐一改进这些方法，从而引入 van Emde Boas 结构的原型，它是递归的、但并未达到 $O(\log \log u)$ 的运行时间。
• （算导20.3节）对原型 van Emde Boas 结构进行改进，发展为 van Emde Boas 树，并且介绍如何在 $O(\log \log u)$ 时间内实现每个操作。

---

1. 基本方法

本节讨论动态集合的几种存储方法。虽然这些操作都无法达到想要的 $O(\log \log u)$ 运行时间界，但这些方法有助于理解后面介绍的 van Emde Boas 树。

1.1 直接寻址

直接寻址（算导11.1节）提供了一种存储动态集合的最简单方法。由于这里只关注存储关键字（如算导11.1-2中讨论过的），可将用于动态集合的直接寻址法、简化为一个位向量。我们维护一个 $u$ 位的数组 $A[0\dots u-1]$ ，以存储一个值来自全域 { 0 , 1 , 2 , … , u − 1 } \{ 0, 1, 2, \dots, u - 1\} {0,1,2,…,u−1} 的动态集合。若值 $x$ 属于动态集合，则元素 $A[x]=1$ ；否则，$A[x]=0$ 。

虽然利用位向量方法可以使 INSERT, DELETE, MEMBER 操作的运行时间为 $O(1)$ ，然而其余操作 MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR 在最坏情况下仍需 $\Theta (u)$ 的运行时间，这是因为操作需要扫描 $\Theta (u)$ 个元素（这里始终假设：如果动态集合为空，则 MINIMUM, MAXIMUM 返回 NULL ；如果给定的元素没有后继或前驱，则 SUCCESSOR, PREDECESSOR 分别返回 NULL）。例如，如果一个集合只包含值 $0,u-1$ ，则要查找 $0$ 的后继，就需要查询 $1$ 到 $u-2$ 的所有结点，直到发现 $A[u-1]$ 中的 $1$ 为止。

1.2 叠加的二叉树结构 Superimposing a binary tree structure

我们能够使用「位向量上方叠加一棵位二叉树」的方法，来缩短对位向量的长扫描。图20-1显示了一个例子。位向量的全部元素组成了二叉树的叶子，并且每个内部结点为 $1$ 当且仅当其子树中任一个叶结点包含 $1$ 。即，内部结点中存储的位，就是其两个孩子的逻辑或。

现在使用这种树结构和未经修饰的位向量 unadorned bit vector ，具有最坏情况运行时间为 $\Theta (u)$ 的操作如下：

• 查找集合中的最小值，从树根开始，箭头朝下指向叶结点，总是走最左边包含 $1$ 的结点。
• 查找集合中的最大值，从树根开始，箭头操作指向叶结点，总是走最右边包含 $1$ 的结点。
• 查找 $x$ 的后继，从 $x$ 所在的叶结点开始，箭头朝上指向树根，直到从左侧进入一个结点，其右孩子结点 $z$ 为 $1$ 。然后从结点 $z$ 出发箭头朝下，始终走最左边包含 $1$ 的结点（即查找以 $z$ 为根的子树中的最小值）。
• 查找 $x$ 的前驱，从 $x$ 所在的叶结点开始，箭头朝上指向树根，直到从右侧进入一个结点，其左孩子结点 $z$ 为 $1$ 。然后从结点 $z$ 出发箭头朝下，始终走最右边包含 $1$ 的结点（即查找以 $z$ 为根的子树中的最大值）。

图20-1显示了查找 $14$ 的前驱 $7$ 所走的路径。

我们也适当地讨论了 INSERT, DELETE 操作。

• 当插入一个值时，从该叶结点到根的简单路径上每个结点都置为 $1$ 。
• 当删除一个值时，从该叶结点出发到根，重新计算这个简单路径上每个内部结点的位值，该值为其两个孩子的逻辑或。

由于树的高度为 $\log u$ ，上面每个操作至多沿树进行一趟向上和一趟向下的过程，因此每个操作的最坏情况运行时间为 $O(\log u)$ 。这种方法仅仅比红黑树好一点。MEMBER 操作的运行时间只有 $O(1)$ ，而红黑树却需要花费 $O(\log n)$ 时间。另外，如果存储的元素个数 $n$ 比全域大小 $u$ 小得多，那么对于所有的其他操作，红黑树要快些。

1.3 叠加的一棵高度恒定的树

如果叠加一棵度更大的树，会发生什么情况？假设全域的大小为 $u=2^{2k}$ ，这里 $k$ 为某个整数，那么 $\sqrt{u}$ 是一个整数。我们叠加一棵度为 $\sqrt{u}$ 的树，来代替位向量上方叠加的二叉树。图20-2(a)展示了这样的一棵树，其中位向量与图20-1中的一样。结果树的高度总是为 $2$ The height of the resulting tree is always 2 。

同以前一样，每个内部结点存储的是其子树的逻辑或，所以深度为 $1$ 的 $\sqrt{u}$ 个内部结点是每组 $\sqrt{u}$ 值的合计（即逻辑或）。如图20-2(b)所示，可以为这些结点定义一个数组 $summary[0\dots \sqrt{u}-1]$ ，其中 $summary[i]$ 包含 $1$ 当且仅当其子数组 $A[i\sqrt{u}\dots (i+1)\sqrt{u}-1]$ 包含 $1$ 。我们称 $A$ 的这个 $\sqrt{u}$ 位子数组为第 $i$ 个簇 cluster 。对于一个给定的值 $x$ ，位 $A[x]$ 出现在簇号为 $\lfloor x/\sqrt{u}\rfloor$ 中。现在，INSERT 变为一个 $O(1)$ 运行时间的操作：要插入 $x$ ，置 $A[x]$ 和 $summary[\lfloor x/\sqrt{u}\rfloor ]$ 为 $1$ 。此外，使用 $summary$ 数组可以在 $O(\sqrt{u})$ 运行时间内、实现 MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR, DELETE 操作：

• 查找最小（最大）值，在 $summary$ 数组中查找最左（最右）包含 $1$ 的项，如 $summary[i]$，然后在第 $i$ 个簇内顺序查找最左（最右）的 $1$ 。
• 查询 $x$ 的后继（前驱），先在 $x$ 的簇中向右（左）查找。如果发现 $1$ ，则返回这个位置作为结果；否则，令 $i=\lfloor x/\sqrt{u}\rfloor$ ，然后从下标 $i$ 开始、在 $summary$ 数组中向右（左）查找。找到第一个包含 $1$ 的位置，就得到这个簇的下标。再在该簇中查找最左（最右）的 $1$ ，这个位置的元素就是后继（前驱）。
• 删除值 $x$ ，设 $i=\lfloor x/\sqrt{u}\rfloor$ 。将 $A[x]$ 置为 $0$ ，然后置 $summary[i]$ 为第 $i$ 个簇中所有位的逻辑或。

在上述的每个操作中，最多对「两个大小为 $\sqrt{u}$ 位的簇」以及 $summary$ 数组进行搜索，所以每个操作耗费 $O(\sqrt{u})$ 时间。

初看起来，似乎并没有取得好的效果。叠加的二叉树得到了时间为 $O(\log u)$ 的操作，其渐近地快于 $O(\sqrt{u})$ 。然而，使用度为 $\sqrt{u}$ 的树，是产生 van Emde Boas 树的关键思想。下一节继续沿着这条路线讨论下去。

---

2. 递归结构

在本节中，我们对「位向量上度为 $\sqrt{u}$ 的叠加树想法」进行修改。上一节中，用到了大小为 $\sqrt{u}$ 的 $summary$ 数组，数组的每项都指向一个大小为 $\sqrt{u}$ 的另一个结构。现在使用结构递归，每次递归都以平方根大小缩减全域。一个全域初始大小为 $u$ ，使用包含 $\sqrt{u}=u^{1/2}$ 项数的结构，其各项又是包含 $u^{1/4}$ 项数的结构，而 $u^{1/4}$ 结构中的每项又是包含 $u^{1/8}$ 项数的结构，依次类推，降低到项数为 $2$ 的基本大小时为止。

为简单起见，本节中假设 $u=2^{2^k}$ ，其中 $k$ 为整数，因此 $u,u^{1/2},u^{1/4},\dots$ 都为整数。这个限制在实际应用中过于严格，因为仅仅只允许 $u$ 的值在序列 $2,4,16,256,65536,\dots$ 中。下一节会看到如何放宽这个假设，而只假定对某个整数 $k$ 、$u=2^k$ 。由于本节描述的结构仅作为真正 van Emde Boas 树的一个准备，为了帮助理解，我们就容忍了这个限制。

注意到，我们的目标是使得这些操作达到 $O(\log \log n)$ 的运行时间，思考如何才能达到这样的运行时间。（在算导4.3节的最后）通过变量替换法，能够得到递归式：$$T(n)=2T(\lfloor \sqrt{n}\rfloor )+\log n\text{\hspace{1em}(20.1)}$$

的解为 $T(n)=O(\log n\log \log n)$ 。考虑一个相似但更简单的递归式：$$T(u)=T(\sqrt{u})+O(1)\text{\hspace{1em}(20.2)}$$

如果使用同样的变量替换方法，则递归式 $(20.2)$ 的解为 $T(u)=O(\log \log u)$ 。令 $m=\log u$ ，那么 $u=2^m$ ，则有：$$T(2^m)=T(2^{m/2})+O(1)$$

现在重命名 $S(m)=T(2^m)$ ，新的递归式为：$$S(m)=S(m/2)+O(1)$$ 应用主方法的情况2，这个递归式的解为 $S(m)=O(\log m)$ 。将 $S(m)$ 变回到 $T(u)$ ，得到：$$T(u)=T(2^m)=S(m)=O(\log m)=O(\log \log u)$$

递归式 $(20.2)$ 将指导数据结构上的查找。我们要设计一个递归的数据结构，该数据结构每层递归以 $\sqrt{u}$ 为因子缩减规模。当一个操作遍历这个数据结构时，在递归到下一层次前，其在每一层耗费常数时间。递归式 $(20.2)$ 刻画了运行时间的这个特征。

这里有另一途径来理解项 $\log \log u$ 如何最终成为递归式 $(20.2)$ 的解。正如我们看到的，每层递归数据结构的全域大小是序列 $u,u^{1/2},u^{1/4},u^{1/8},\dots$ 。如果考虑每层需要多少位来存储全域，那么顶层需要 $\log u$ ，而后面每一层需要前一层的一半位数。一般来说，如果以 $b$ 位开始并且每层减少一半的位数，那么 $\log b$ 层递归之后，只剩下一位。因为 $b=\log u$ ，那么 $\log \log u$ 层之后，全域大小就为 $2$ 。

现在回头来看图20-2中的数据结构，一个给定的值 $x$ 在簇编号 $\lfloor x/\sqrt{u}\rfloor$ 中。如果把 $x$ 看做是 $\log u$ 位的二进制整数，那么簇编号 $\lfloor x/\sqrt{u}\rfloor$ 由 $x$ 中最高 $(\log u)/2$ 位来决定。在 $x$ 簇中，$x$ 出现在位置 $x\mathrm{m}\mathrm{o}\mathrm{d}\sqrt{u}$ 中，是由 $x$ 中最低 $(\log u)/2$ 位决定。后面需要这种方式处理下标，因此定义以下一些函数将会有用。
$$\begin{array}{rl}& high(x)=\lfloor x/\sqrt{u}\rfloor \\ & low(x)=x\mathrm{m}\mathrm{o}\mathrm{d}\sqrt{u}\\ & index(x,y)=x\sqrt{u}+y\end{array}$$

函数 $high(x)$ 给出了 $x$ 的最高 $(\log u)/2$ 位，即为 $x$ 的簇号。函数 $low(x)$ 给出了 $x$ 的最低 $(\log u)/2$ 位，即为 $x$ 在它自己簇中的位置。函数 $index(x,y)$ 从 $x,y$ 产生一个元素编号，其中 $x$ 为元素编号中最高 $(\log u)/2$ 位，$y$ 为元素编号中最低 $(\log u)/2$ 位。我们有恒等式 $x=index(high(x),low(x))$ 。这些函数中使用的 $u$ 值，始终为调用这些函数的数据结构的全域大小，$u$ 的值随递归结构改变。

2.1 原型 van Emde Boas 结构

根据递归式 $(20.2)$ 中的启示，我们设计一个递归数据结构来支持这些操作。虽然这个数据结构对于某些操作达不到 $O(\log \log u)$ 运行时间的目标，但它可以作为（将在20.3节中看到的）van Emde Boas 树的基础。

对于全域 { 0 , 1 , 2 , … , u − 1 } \{ 0, 1, 2, \dots, u - 1\} {0,1,2,…,u−1} ，定义原型 van Emde Boas 结构 proto van Emde Boas structure 或者 proto-vEB 结构 proto-vEB structure ，记作 $\text{proto-vEB(u)}$ ，可以如下递归定义。每个 $\text{proto-vEB(u)}$ 结构都包含一个给定全域大小的属性 $u$ 。另外，它包含以下特征：

• 如果 $u=2$ ，那么它是基础大小，只包含一个两个位的数组 $A[0\dots 1]$ 。
• 否则，对某个整数 $k\ge 1$ ，$u=2^{2^k}$ ，于是有 $u\ge 4$ 。除了全域大小 $u$ 之外， $\text{proto-vEB(u)}$ 还具有以下属性（如图20-3所示）。
  • 一个名为 $summary$ 的指针，指向一个 $\text{proto-}\mathrm{v}\mathrm{E}\mathrm{B}(\sqrt{\mathrm{u}})$ 结构。
  • 一个数组 $cluster[0\dots \sqrt{u}-1]$（中文版印错了！），存储 $\sqrt{u}$ 个指针，每个指针都指向一个 $\text{proto-}\mathrm{v}\mathrm{E}\mathrm{B}(\sqrt{\mathrm{u}})$ 结构。元素 $x$（这里 $0\le x<u$）递归地存储在编号为 $high(x)$ 的簇中，作为该簇中编号为 $low(x)$ 的元素 。
    

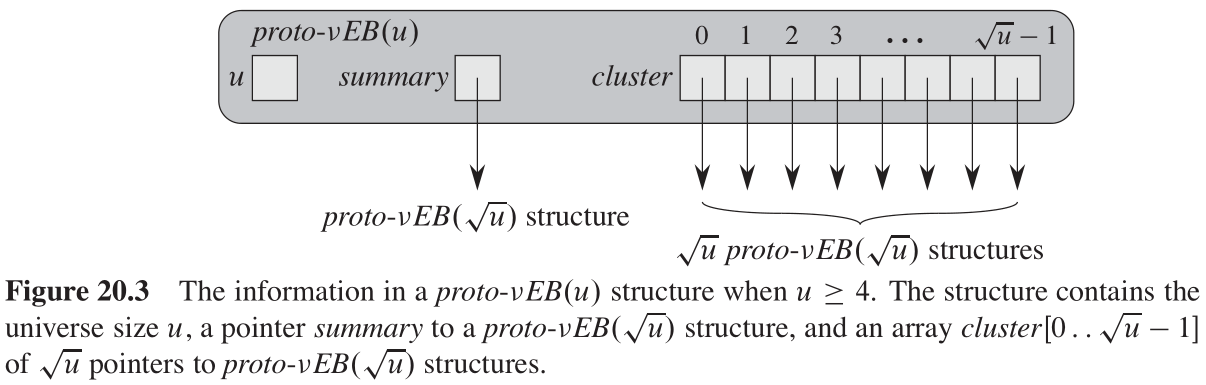
在前一节的二层结构中，每个结点存储一个大小为 $\sqrt{u}$ 的 $summary$ 数组，其中每个元素包含一个位。从每个元素的下标，我们可以计算出大小为 $\sqrt{u}$ 的子数组的开始下标 From the index of each entry, we can compute the starting index of the subarray of size sqrt(u) that the bit summarizes 。而在 $\text{proto-vEB}$ 结构中，我们使用显式指针、而非下标计算的方法。$summary$ 数组包含了 $\text{proto-vEB}$ 结构中递归存储的 $summary$ 位向量，并且 cluster 数组包含了 $\sqrt{u}$ 个指针。

图20-4展示了一个完全展开的 $\text{proto-vEB(16)}$ 结构，它表示集合 { 2 , 3 , 4 , 5 , 7 , 14 , 15 } \{ 2, 3, 4, 5, 7, 14, 15\} {2,3,4,5,7,14,15} 。如果值 $i$ 在由 $summary$ 指向的 $\text{proto-vEB}$ 结构中，那么第 $i$ 个簇包含了被表示集合中的某个值。与常数高度的树一样，$cluster[i]$ 表示 $i\sqrt{u}$ 到 $(i+1)\sqrt{u}-1$ 的那些值，这些值形成了第 $i$ 个簇。

在基础层上，实际动态集合的元素被存储在一些 $\text{proto-vEB(2)}$ 结构中，而余下的 $\text{proto-vEB(2)}$ 结构则存储 $summary$ 位向量。在每个非 $summary$ 基础结构 non-summary base structures 的底部，数字表示它存储的位。例如，标记为 element 6, 7 的 $\text{proto-vEB(2)}$ 结构在 $A[0]$ 中存储位 $6$（ $0$ ，因为元素 $6$ 不在集合中），并在 $A[1]$ 中存储位 $7$（ $1$ ，因为元素 $7$ 在集合中）。

与簇一样，每个 $summary$ 只是一个全域大小为 $\sqrt{u}$ 的动态集合，而且每个 $summary$ 表示为一个 $\text{proto-}\mathrm{v}\mathrm{E}\mathrm{B}(\sqrt{\mathrm{u}})$ 结构。主 $\text{proto-vEB(16)}$ 结构的四个 $summary$ 位都在最左侧的 $\text{proto-vEB(4)}$ 结构中，并且它们最终出现在 $2$ 个 $\text{proto-vEB(2)}$ 结构中。例如，标记为 clusters 2, 3 的 $\text{proto-vEB(2)}$ 结构有 $A[0]=0$ ，含义为 $\text{proto-vEB(16)}$ 结构的簇 $2$（包含元素 $8,9,10,11$ ）都为 $0$ ；并且 $A[1]=1$ ，说明 $\text{proto-vEB(16)}$ 结构的簇 $3$（包含元素 $12,13,14,15$ ）至少有一个为 $1$ 。

每个 $\text{proto-vEB(4)}$ 结构都指向自身的 $summary$ ，而 $summary$ 自己存储为一个 $\text{proto-vEB(2)}$ 结构 Each proto-vEB(4) structure points to its own summary, which is itself stored as a proto-vEB(2) structure 。例如，查看标为 element 0, 1 结构左侧的那个 $\text{proto-vEB(2)}$ 结构。因为 $A[0]=0$ ，所以 elements 0, 1 结构都为 $0$ ；由于 $A[1]=1$ ，因此 elements 2, 3 结构至少有一个 $1$ 。

2.2 原型 van Emde Boas 结构上的操作

下面将讨论如何在一个 $\text{proto-vEB}$ 结构上执行一些操作。先看查询操作 MEMBER, MINIMUM, MAXIMUM, SUCCESSOR ，这些操作不改变 $\text{proto-vEB}$ 结构。接下来讨论 INSERT, DELETE 操作。另外，留下 MAXIMUM, PREDECESSOR 操作作为（算导练习20.2-1）。它们分别与 MINIMUM, SUCCESSOR 是对称的。

MEMBER, SUCCESSOR, PREDECESSOR, INSERT, DELETE 操作都取一个参数 $x$ 和一个 $\text{proto-vEB}$ 结构 $V$ 作为输入参数。这些操作均假定 $0\le x<V.u$ 。

判断一个值是否在集合中

要实现 MEMBER(x) 操作，就需要在一个适当的 $\text{proto-vEB(2)}$ 结构中找到相应于 $x$ 的位。借助全部的 $summary$ 结构，这个操作能够在 $O(\log \log u)$ 时间内完成。下面的过程以一个 $\text{proto-vEB}$ 结构 $V$ 和一个值 $x$ 作为输入，返回一个位值表示 $x$ 是否在 $V$ 包含的动态集合中。

PROTO-vEB-MEMBER(V, x)
	if V.u == 2
		return V.A[x]
	else return PROTO-vEB-MEMBER(V.cluster[ high(x) ], low(x))

PROTO-vEB-MEMBER(V, x) 过程工作如下。第 $1$ 行测试是否为基础情形，其中 $V$ 是一个 $\text{proto-vEB(2)}$ 结构；第 $2$ 行处理基础情形，简单地返回数组 $A$ 的一个相应位。第 $3$ 行处理递归情形，“钻入”到相应更小的 $\text{proto-vEB}$ 结构——值 $high(x)$ 表示要访问的 $\text{proto-vEB(}\sqrt{\mathrm{u}}\text{)}$ 结构，值 $low(x)$ 表示要查询的 $\text{proto-vEB(}\sqrt{\mathrm{u}}\text{)}$结构中的元素。

在图20-4中，我们看一下在 $\text{proto-vEB(}16\text{)}$ 结构中调用 PROTO-vEB-MEMBER(V, 6) 会发生什么。由于当 $u=16$ 时，$high(6)=1$ ，则递归到右上方的 $\text{proto-vEB(4)}$ 结构，并且查询该结构中的元素 $low(6)=2$ 。在这次递归调用中，$u=4$ ，这样还需要进行递归。对于 $u=4$ ，就有 $high(2)=1$ 和 $low(2)=0$ ，所以要查询右上方的 $\text{proto-vEB(2)}$ 结构中的元素 $0$ 。这样递归调用就到了基础情形，所以通过递归调用链返回 $A[0]=0$ 。因此，得到 PROTO-vEB-MEMBER(V, 6) 返回 $0$ 的结果，表示 $6$ 不在集合内。

为了确定 PROTO-vEB-MEMBER 的运行时间，令 $T(u)$ 表示 $\text{proto-vEB(u)}$ 结构上的运行时间。每次递归调用耗费常数时间，其不包括由递归调用自身所产生的时间。当 PROTO-vEB-MEMBER 做一次递归调用时，它在 $\text{proto-vEB(}\sqrt{\mathrm{u}}\text{ )}$ 结构上产生一次调用。因此，运行时间可以用递归表达式 $T(u)=T(\sqrt{u})+O(1)$ 表示，该递归式就是前面的递归式 $(20.2)$ 。它的解为 $T(u)=O(\log \log u)$ ，所以 PROTO-vEB-MEMBER 的运行时间为 $O(\log \log u)$ 。

查找最小元素

现在我们讨论如何实现 MINIMUM 操作。过程 PROTO-vEB-MINIMUM(V) 返回 $\text{proto-vEB}$ 结构 $V$ 中的最小元素；如果 $V$ 代表的是一个空集，则返回 NULL 。

PROTO-vEB-MINIMUM(V)
	if V.u == 2
		if V.A[0] == 1
			return 0
		else if V.A[1] == 1
			return 1
		else return NULL
	else min-cluster = PROTO-vEB-MINIMUM(V.summary)
		if min-cluster == NULL
			return NULL
		else offset = PROTO-vEB-MINIMUM(V.cluster[ min-cluster ])
			return index(min-cluster, offset)

这个过程工作如下。

• 第 $1$ 行判断是否为基础情形，第 $2\sim 6$ 行平凡地处理基础情形。
• 第 $7\sim 11$ 行处理递归情形。首先，第 $7$ 行查找包含集合元素的第一个簇号。做法是通过在 $V.summary$ 上递归调用 PROTO-vEB-MINIMUM 来进行，其中 $V.summary$ 是一个 $\text{proto-vEB(}\sqrt{\mathrm{u}}\text{)}$ 结构。第 $7$ 行将这个簇号赋值给变量 $\text{min-cluster}$ 。如果集合为空，那么递归调用返回 NULL ，第 $9$ 行返回 NULL 。如果集合非空，集合的最小元素就存在于编号为 $\text{min-cluster}$ 的簇中。第 $10$ 行中的递归调用是查找最小元素在这个簇中的偏移量。最后，第 $11$ 行由簇号和偏移量来构造这个最小元素的值，并返回。

虽然查找 $summary$ 信息允许我们快速地找到包含最小元素的簇，但是由于这个过程需要两次调用 $\text{proto-vEB(}\sqrt{\mathrm{u}}\text{)}$ 结构，所以在最坏情况下运行时间超过 $O(\log \log u)$ 。令 $T(u)$ 表示在 $\text{proto-vEB(u)}$ 结构上的、PROTO-vEB-MINIMUM 操作的最坏情况运行时间，有下面递归式：$$T(u)=2T(\sqrt{u})+O(1)\text{\hspace{1em}(20.3)}$$

再一次利用变量替换法来求解此递归式，令 $m=\log u$ ，可以得到：$$T(2^m)=2T(2^{m/2})+O(1)$$

重命名为 $S(m)=T(2^m)$ ，得到：$$S(m)=2S(m/2)+O(1)$$

利用主方法的情况1，解得 $S(m)=\Theta (m)$ 。将 $S(m)$ 换回为 $T(u)$ ，可以得到 $T(u)=T(2^m)=S(m)=\Theta (m)=\Theta (\log u)$ 。因此，由于有第二个递归调用，PROTO-vEB-MINIMUM 的运行时间为 $\Theta (\log u)$ ，而不是 $\Theta (\log \log u)$ 。

查找后继

SUCCESSOR 的运行时间更长。在最坏情况下，它需要做两次递归调用和一次 PROTO-vEB-MINIMUM 调用。过程 PROTO-vEB-SUCCESSOR(V, x) 返回 $\text{proto-vEB}$ 结构 $V$ 中大于 $x$ 的最小元素；或者，如果 $V$ 中不存在大于 $x$ 的元素，则返回 NULL 。它不要求 $x$ 一定属于该集合，但假定 $0\le x<V.u$ 。

PROTO-vEB-SUCCESSOR(V, x)
	if V.u == 2
		if x == 0 and V.A[1] == 1
			return 1
		else return NULL
	else offset = PROTO-vEB-SUCCESSOR(V.cluster[ high(x) ], low(x))
		if offset != NULL
			return index(high(x), offset)
		else succ-cluster = PROTO-vEB-SUCCESSOR(V.summary, high(x))
			if succ-cluster == NULL
				return NULL
			else offset = PROTO-vEB-MINIMUM(V.cluster[ succ-cluster ])
				return index(succ-cluster, offset)

PROTO-vEB-SUCCESSOR 过程工作如下。与通常一样，第 $1$ 行判断是否为基础情形，第 $2\sim 4$ 行平凡处理：当 $x=0$ 和 $A[1]=1$ 时，才能在 $\text{proto-vEB(2)}$ 结构中找到 $x$ 的后继。第 $5\sim 12$ 行处理递归情形。第 $5$ 行在 $x$ 的簇内查找其后继，并将结果赋给变量 $offset$ 。第 $6$ 行判断这个簇中是否存在 $x$ 的后继；若存在，第 $7$ 行计算并返回其值，否则必须在其他簇中查找。

第 $8$ 行将下一个非空簇号赋给变量 $\text{succ-cluster}$ ，并利用 $summary$ 信息来查找后继。第 $9$ 行判断 $\text{succ-cluster}$ 是否为 NULL ，如果所有后继簇是空的，第 $10$ 行返回 NULL 。如果 $\text{succ-cluster}$ 不为 NULL ，第 $11$ 行将编号为 $\text{succ-cluster}$ 的簇中第一个元素赋值给 $offset$ ，并且第 $12$ 行计算并返回这个簇中的最小元素。

在最坏情况下，PROTO-vEB-SUCCESSOR 在 $\text{proto-vEB(}\sqrt{\mathrm{u}}\text{)}$ 结构上做 $2$ 次自身递归调用和 $1$ 次 PROTO-vEB-MINIMUM 调用。所以，最坏情况下，PROTO-vEB-SUCCESSOR 的运行时间用下面的递归式表示：$$T(u)=2T(\sqrt{u})+\Theta (\log \sqrt{u})=2T(\sqrt{u})+\Theta (\log u)$$

可以用求解递归式 $(20.1)$ 的方法来得出上面递归式的解 $T(u)=\Theta (\log u\log \log u)$ 。因此，PROTO-vEB-SUCCESSOR 是渐近地慢于 PROTO-vEB-MINIMUM 。

插入元素

要插入一个元素，需要将其插入相应的簇中，并且还要将这个簇中的 $summary$ 位设为 $1$ 。过程 PROTO-vEB-INSERT(V, x) 将 $x$ 插入 $\text{proto-vEB}$ 结构 $V$ 中。

PROTO-vEB-INSERT(V, x)
	if V.u == 2
		V.A[x] = 1
	else PROTO-vEB-INSERT(V.cluster[ high(x) ], low(x))
		PROTO-vEB-INSERT(V.summary, high(x))

在基础情形中，第 $2$ 行把数组 $A$ 中的相应位设为 $1$ 。在递归情形中，第 $3$ 行的递归调用将 $x$ 插入相应的簇中，并且第 $4$ 行把该簇中的 $summary$ 位置为 $1$ 。

因为 PROTO-vEB-INSERT 在最坏情况下做 $2$ 次递归调用，其运行时间可由递归式 $(20.3)$ 来表示。所以，PROTO-vEB-INSERT 的运行时间为 $\Theta (\log u)$ 。

删除元素

删除操作比插入操作要更复杂些。当插入新元素时，插入时总是将一个 $summary$ 位置为 $1$ ，然而删除时却不总是将同样的 $summary$ 位置为 $0$ 。我们需要判断相应的簇中是否存在为 $1$ 的位。对于已定义的 $\text{proto-vEB}$ 结构，本来需要检查簇内的所有 $\sqrt{u}$ 位是否为 $1$ 。取而代之的是，可以在 $\text{proto-vEB}$ 结构中添加一个属性 $n$ ，来记录其拥有的元素个数。把 PROTO-vEB-DELETE 的实现留为（算导练习20.2-2和练习20.2-3）。

很显然，必须要修改 $\text{proto-vEB}$ 结构，使得每个操作降至至多只进行一次递归调用。下一节将讨论如何去做。

---

3. van Emde Boas 树及其操作

前一节中的 $\text{proto-vEB}$ 结构已经接近运行时间为 $O(\log \log u)$ 的目标。其缺陷是大多数操作要进行多次递归。本节中我们要设计一个类似于 $\text{proto-vEB}$ 结构的数据结构，但要存储稍多一些的信息，由此可以去掉一些递归的需求。

（算导20.2节中）注意到，针对全域大小 $u=2^{2^k}$ ，其中 $k$ 为整数，此假设有非常大的局限性，$u$ 的可能值为一个非常稀疏的集合。因此从这点上，我们将允许全域大小 $u$ 为任何一个 $2$ 的幂，而且当 $\sqrt{u}$ 不为整数（即 $u$ 为 $2$ 的奇数次幂 $u=2^{2k+1}$ ，其中某个整数 $k\ge 0$ ）时，把一个数的 $\log u$ 位分割成最高 $\lceil (\log u)/2\rceil$ 位和最低 $\lfloor (\log u)/2\rfloor$ 位。为方便起见，把 $2^{\lceil (\log u)/2\rceil }$ 记为 $\sqrt[\uparrow ]{u}$（ $u$ 的上平方根），$2^{\lfloor (\log u)/2\rfloor }$ 记为 $\sqrt[\downarrow ]{u}$（ $u$ 的下平方根），于是有 $u=\sqrt[\uparrow ]{u}\cdot \sqrt[\downarrow ]{u}$ 。当 $u$ 为 $2$ 的偶数次幂（$u=2^{2k}$ ，其中 $k$ 为某个整数）时，有 $\sqrt[\uparrow ]{u}=\sqrt[\downarrow ]{u}=\sqrt{u}$ 。

由于现在允许 $u$ 是一个 $2$ 的奇数次幂，（从算导20.2节中）重新定义一些有用的函数：
$$\begin{array}{rl}high(x)& =\lfloor x/\sqrt[\downarrow ]{u}\rfloor \\ low(x)& =x\mathrm{m}\mathrm{o}\mathrm{d}\sqrt[\downarrow ]{u}\\ index(x,y)& =x\sqrt[\downarrow ]{u}+y\end{array}$$

3.1 van Emde Boas 树

van Emde Boas 树或 vEB 树是在 $\text{proto-vEB}$ 结构的基础上修改而来的。我们将全域大小为 $u$ 的 vEB 树记为 vEB(u) 。如果 $u$ 不为 $2$ 的基础情形，那么属性 $summary$ 指向一棵 $vEB(\sqrt[\uparrow ]{u})$ 树，而且数组 $cluster[0\dots \sqrt[\uparrow ]{u}-1]$ 指向 $\sqrt[\uparrow ]{u}vEB(\sqrt[\downarrow ]{u})$ 棵树。如图20-5所示，一棵 vEB 树含有 $\text{proto-vEB}$ 结构中没有的两个属性：

• $min$ 存储 vEB 树中的最小元素；
• $max$ 存储 vEB 树中的最大元素。
  

进一步地，存储在 $min$ 中的元素并不出现在任何递归的 $vEB(\sqrt[\downarrow ]{u})$ 树中，这些树是由 $cluster$ 数组指向它们的，因此在 $vEB(u)$ 树 $V$ 中存储的元素为 $V.min$ 、再加上由 $V.cluster[0\dots \sqrt[\uparrow ]{u}-1]$ 指向的递归存储在 $vEB(\sqrt[\downarrow ]{u})$ 树中的元素。注意到，当一棵 vEB 树中包含两个或两个以上的元素时，我们以不同方式处理 $min$ 和 $max$ ：存储在 $min$ 中的元素不出现在任何簇中，而存储在 $max$ 中的元素却不是这样。

因为基础情形的大小为 $2$ ，这样一棵 $vEB(2)$ 树中的、相应 $\text{proto-vEB(2)}$ 结构并不需要数组 $A$ 。然而，我们可以从其 $min$ 和 $max$ 属性来确定它的元素。在一棵不包含任何元素的 vEB 树中，不管全域的大小 $u$ 如何，$min$ 和 $max$ 均为 NULL 。

图20-6显示了一棵 $vEB(16)$ 树 $V$ ，包含集合 { 2 , 3 , 4 , 5 , 7 , 14 , 15 } \{ 2, 3, 4, 5, 7, 14, 15\} {2,3,4,5,7,14,15} 。因为最小的元素是 $2$ ，所以 $V.min$ 等于 $2$ ，而且即使 $high(2)=0$ ，元素 $2$ 也不会出现在由 $V.cluster[0]$ 所指向的 $vEB(4)$ 树中：注意到 $V.cluster[0].min$ 等于 $3$ ，因此元素 $2$ 不在这棵 vEB 树中。类似地，因为 $V.cluster[0].min$ 等于 $3$ ，而且 $V.cluster[0]$ 中只包含元素 $2,3$ ，所以 $V.cluster[0]$ 内的 $vEB(2)$ 簇为空。

$min$ 和 $max$ 属性是减少 vEB 树上这些操作的递归调用次数的关键。这两个属性有四个方面的作用：

1. MINIMUM, MAXIMUM 操作甚至不需要递归，因为可以直接返回 $min,max$ 的值。
2. SUCCESSOR 操作可以避免一个「用于判断 $x$ 的后继是否位于 $high(x)$ 簇中」的递归调用。这是因为 $x$ 的后继位于 $x$ 簇中，当且仅当 $x$ 严格小于 $x$ 所在簇的 $max$ 。对于 PREDECESSOR 和 $min$ 情况，可以对照得到。
3. 通过 $min,max$ 的值，可以在常数时间内告知一棵 vEB 树是否为空、仅含一个元素或两个以上元素。这种能力将在 INSERT, DELETE 操作中发挥作用。
   • 如果 $min,max$ 都为 NULL ，那么 vEB 树为空。
   • 如果 $min,max$ 都不为 NULL 但彼此相等，那么 vEB 树仅含一个元素。
   • 如果 $min,max$ 都不为 NULL 且不等，那么 vEB 包含两个或两个以上元素。
4. 如果一棵 vEB 树为空，那么可以仅更新它的 $min$ 和 $max$ 值来实现插入一个元素。因此，可以在常数时间内向一棵空 vEB 树中插入元素。类似地，如果一棵 vEB 树仅含一个元素，也可以仅更新 $min,max$ 值、在常数时间内删除这个元素。这些性质可以缩减递归调用链。

即使全域大小 $u$ 为 $2$ 的奇数次幂，「 vEB 树中 $summary$ 和 clusteer 大小的差异」不会影响操作的渐近运行时间。实现 vEB 树操作的递归过程的运行时间，可由下面递归式来刻画：
$$T(u)\le T(\sqrt[\uparrow ]{u})+O(1)\text{\hspace{1em}(20.4)}$$

这个递归式与式 $(20.2)$ 相似，我们用类似的方法求解它。令 $m=\log u$ ，重写为：
$$T(2^m)\le T(2^{\lceil m/2\rceil })+O(1)$$

注意到，对所有 $m\ge 2$ ，$\lceil m/2\rceil \le 2m/3$ ，可以得到：$$T(2^m)\le T(2^{2m/3})+O(1)$$

令 $S(m)=T(2^m)$ ，上式重写为：
$$S(m)\le S(2m/3)+O(1)$$

根据主方法的情况2，有解 $S(m)=O(\log m)$（对于渐近解，分数 $2/3$ 与 $1/2$ 没有任何差别，因为应用主方法时，得到 ${\log }_{3/2}1={\log }_{2}1=0$ ）。于是我们有：$$T(u)=T(2^m)=S(m)=O(\log m)=O(\log \log u)$$

在使用 van Emde Boas 树之前，一定要知道全域大小 $u$ ，这样才能够创建一个大小合适且初始为空的 van Emde Boas 树。（正如算导思考题20-1说明的）一棵 van Emde Boas 树的总空间需求是 $O(u)$ ，直接地创建一棵空 vEB 树需要 $O(u)$ 时间。相反，红黑树的建立只需常数时间。因此，不应使用一棵 van Emde Boas 树用于仅仅执行少数操作的情况，因为建立数据结构的时间要超过单个操作节省的时间。这个缺点并不严重，我们通常可以使用像数组或链表这样简单的数据结构来存储少量数据。

3.2 van Emde Boas 树的操作

现在来介绍 van Emde Boas 树的操作。与原型 van Emde Boas 结构所做的一样，首先介绍查找操作，然后是 INSERT, DELETE 操作。由于在一棵 vEB 树中最小元素和最大元素之间的不对称性（当一棵 vEB 树至少包含两个元素时，最小元素不出现在簇中，而最大元素在簇中），我们会给出所有五个查询操作的伪代码。正如原型 van Emde Boas 结构上的操作，这里操作取输入参数 $V$ 和 $x$ ，其中 $V$ 是一棵 van Emde Boas 树，$x$ 是一个元素，假定 $0\le x<V.u$ 。

查找最小元素和最大元素

因为最小元素和最大元素分别存储在 $min$ 和 $max$ 属性中，所以两个操作均只有一行代码，耗费常数时间：

vEB-TREE-MINIMUM(V)
	return V.min
vEB-TREE-MAXIMUM(V)
	return V.max

判断一个值是否在集合中

过程 vEB-TREE-MEMBE(V, x) 有一个递归情形，其与 PROTO-vEB-MEMBER 中的类似，然而基础情形却稍微不同。我们仍然会直接检查 $x$ 是否等于最小元素或最大元素。由于 vEB 树并不像 proto-vEB 结构那样存储位信息，所以设计 vEB-TREE-MEMBER 返回 true, false 而不是 $0,1$ 。

vEB-TREE-MEMBER(V, x)
	if x == V.min or x == V.max
		return true
	else if V.u == 2
		return false
	else return vEB-TREE-MEMBER(V.cluster[ high(x) ], low(x))

第 $1$ 行判断 $x$ 是否与最小元素或者最大元素相等。如果是，第 $2$ 行返回 true ；否则第 $3$ 行检查基础情形。因为一棵 vEB(2) 树中除了 $min,max$ 中的元素外，不包含其他元素，所以如果为基础情形，第 $4$ 行返回 false 。另一种可能就是不是基础情形，且 $x$ 既不等于 $min$ 也不等于 $max$ ，这时由第 $5$ 行中的递归调用来处理。

递归式 $(20.4)$ 表明了过程 vEB-TREE-MEMBER 的运行时间，这个过程的运行时间为 $O(\log \log u)$ 。

查找后继和前驱

接下来介绍如何实现 SUCCESSOR 操作。回想过程 PROTO-vEB-SUCCESSOR(V, x) 要进行两个递归调用：一个是判断 $x$ 的后继是否和 $x$ 一样、被包含在 $x$ 的簇中；如果不包含，另一个递归调用就是要找出包含 $x$ 后继的簇。由于能在 vEB 树中很快地访存最大值，这样可以避免进行两次递归调用，并且使一次递归调用或是簇上的、或是 $summary$ 上的，并非两者同时进行。

vEB-TREE-SUCCESSOR(V, x)
	if V.u == 2
		if x == 0 and V.max == 1
			return 1
		else return NULL
	else if V.min != NULL and x < V.min
		return V.min
	else max-low = vEB-TREE-MAXIMUM(V.cluster[ high(x) ])
		if max-low != NULL and low(x) < max-low
			offset = vEB-TREE-SUCCESSOR(V.cluster[ high(x) ], low(x))
			return index(high(x), offset)
		else succ-cluster = vEB-TREE-SUCCESSOR(V.summary, high(x))
			if succ-cluster == NULL
				return NULL
			else offset = vEB-TREE-MINIMUM(V.cluster[ succ-cluster ]) // 后继簇的最小值
				return index(succ-cluster, offset)

这个过程有六个返回语句和几种情形处理。

• 第 $2\sim 4$ 行处理基础情形，如果查找的是 $0$ 的后继、并且 $1$ 在元素 $2$ 的集合中，那么第 $3$ 行返回 $1$ ；否则第 $4$ 行返回 NULL 。
• 如果不是基础情形，下面第 $5$ 行判断 $x$ 是否严格小于最小元素。如果是，那么第 $6$ 行返回这个最小元素。
• 如果进入第 $7$ 行，那么不属于基础情形，并且 $x$ 大于或等于 vEB 树 $V$ 中的最小元素值。第 $7$ 行把 $x$ 簇中的最大元素赋给 $\text{max-low}$ 。如果 $x$ 簇存在大于 $x$ 的元素，那么可确定 $x$ 的后继就在 $x$ 簇中。第 $8$ 行测试这种情况。如果 $x$ 的后继在 $x$ 簇内，那么第 $9$ 行确定 $x$ 的后继在簇中的位置。第 $10$ 行采用与 PROTO-vEB-SUCCESSOR 第 $7$ 行相同的方式返回后继。
• 如果 $x$ 大于等于 $x$ 簇中的最大元素，则进入第 $11$ 行。在这种情况下，第 $11\sim 15$ 行采用与 PROTO-vEB-SUCCESSOR 中第 $8\sim 12$ 行相同的方式查找 $x$ 的后继。

递归式 $(20.4)$ 为 vEB-TREE-SUCCESSOR 的运行时间，这很容易明白。根据第 $7$ 行测试的结果，过程在第 $9$ 行（在全域大小为 $\sqrt[\downarrow ]{u}$ 的 vEB 树上）或者第 $11$ 行（在全域大小为 $\sqrt[\uparrow ]{u}$ 的 vEB 树上）对自身进行递归调用。在两种情况下，一次递归调用是在全域大小至多为 $\sqrt[\uparrow ]{u}$ 的 vEB 树上进行的。过程的剩余部分，包括调用 vEB-TREE-MINIMUM 和 vEB-TREE-MAXIMUM ，耗费时间为 $O(1)$ 。所以 vEB-TREE-SUCCESSOR 的最坏情况运行时间为 $O(\log \log u)$ 。

vEB-TREE-PREDECESSOR 过程与 vEB-TREE-SUCCESSOR 是对称的，但是多了一种附加情况：

vEB-TREE-PREDECESSOR(V, x)
	if V.u == 2
		if x == 1 and V.min == 0
			return 0
		else return NULL
	else if V.max != NULL and x > V.max
		return V.max
	else min-low = vEB-TREE-MINIMUM(V.cluster[ high(x) ])
		if min-low != NULL and low(x) > min-low
			offset = vEB-TREE-PREDECESSOR(V.cluster[ high(x) ], low(x))
			return index(high(x), offset)
		else pred-cluster = vEB-TREE-PREDECESSOR(V.summary, high(x))
			if pred-cluster == NULL
				if V.min != NULL and x > V.min // 13
					return V.min // 14
				else return NULL
			else offset = vEB-TREE-MAXIMUM(V.cluster[ pred-cluster ]) // 前驱簇的最大值
				return index(pred-cluster, offset)

第 $13\sim 14$ 行就是处理这个附加情况。这个附加情况出现在 $x$ 的前驱存在，而不在 $x$ 的簇中。在 vEB-TREE-SUCCESSOR 中，如果 $x$ 的后继不在 $x$ 簇中，那么断定它一定在一个更高编号的簇中。但是如果 $x$ 的前驱是 vEB 树 $V$ 中的最小元素，那么前驱（书上是后继？）不存在于任何一个簇中。第 $13$ 行就是检查这个条件，而且第 $14$ 行返回最小元素。

与 vEB-TREE-SUCCESSOR 相比，这个附加情况并不影响 vEB-TREE-PREDECESSOR 的渐近运行时间，所以它的最坏情况运行时间为 $O(\log \log u)$ 。

插入一个元素

现在讨论如何向一棵 vEB 树中插入一个元素。回想 PROTO-vEB-INSERT 操作进行两次递归调用：一次是插入元素，另一次是将元素的簇号插入 $summary$ 中。然而 vEB-TREE-INSERT 只进行一次递归调用。怎样才能做到只用一次递归呢？当插入一个元素时，在操作的簇中要么已经包含另一个元素，要么不包含任何元素。如果簇中已包含另一个元素，那么簇的编号已存在于 $summary$ 中，因此我们不需要做那次递归调用。如果簇中不包含任何元素，那么即将插入的元素成为簇中唯一的元素，所以我们不需要进行一次递归来将元素插入一棵空 vEB 树中 we do not need to recurse to insert an element into an empty vEB tree ：

vEB-EMPTY-TREE-INSERT(V, x)
	V.min = x
	V.max = x

利用上面这个过程，这里给出 vEB-TREE-INSERT(V, x) 的伪代码，假设 $x$ 不在 vEB 树 $V$ 所表示的集合中：

vEB-TREE-INSERT(V, x)
	if V.min == NULL
		vEB-EMPTY-TREE-INSERT(V, x)
	else if x < V.min // star
			exchange x with V.min
		 if V.u > 2
			if vEB-TREE-MINIMUM(V.cluster[ high(x) ]) == NULL
				vEB-TREE-INSERT(V.summary, high(x))
				vEB-EMPTY-TREE-INSERT(V.cluster[ high(x) ], low(x))
			else vEB-TREE-INSERT(V.cluster[ high(x) ], low(x))
		 if x > V.max
			V.max = x

这个过程的工作如下。

• 第 $1$ 行判断 $V$ 是否是一棵空 vEB 树，如果是，第 $2$ 行处理这种比较简单的情况。
• 第 $3\sim 11$ 行假设 $V$ 非空，因此某个元素会被插入 $V$ 中的一个簇中。而这个元素不一定是通过参数传递进来的元素 $x$ 。如果 $x<min$ ，如第 $3$ 行，那么 $x$ 需要作为新的 $min$ 。然而旧的 $min$ 元素也应该保留，所以旧的 $min$ 元素需要被插入 $V$ 中某个簇中。在这种情况下，第 $4$ 行对 $x$ 和 $min$ 互换，这样将旧的 $min$ 元素插入 $V$ 的某个簇中。
• 仅当 $V$ 不是一棵基础情形的 vEB 树时，第 $6\sim 9$ 行才会被执行。第 $6$ 行判断 $x$ 簇是否为空。如果是，第 $7$ 行将 $x$ 的簇号插入 $summary$ 中，第 $8$ 行处理将 $x$ 插入空簇中的这种简单情况。如果 $x$ 簇已经非空，则第 $9$ 行将 $x$ 插入它的簇中。在这种情况，无需更新 $summary$ ，因为 $x$ 的簇号已经存在于 $summary$ 中。
• 最后，如果 $x>max$ ，那么第 $10\sim 11$ 行更新 $max$ 。注意到，如果 $V$ 是一棵非空的基础情形下的 vEB 树，那么第 $3\sim 4$ 行和第 $10\sim 11$ 行相应地更新 $min$ 和 $max$ 。

这里我们也能容易明白，vEB-TREE-INSERT 的运行时间可以用递归式 $(20.4)$ 表示。根据第 $6$ 行的判断结果，或者执行第 $7$ 行（在全域大小为 $\sqrt[\uparrow ]{u}$ 的 vEB 树上）中的递归调用，或者执行第 $9$ 行（在全域大小为 $\sqrt[\downarrow ]{u}$ 的 vEB 树上）中的递归调用。在两种情况下，其中一个递归调用是在全域大小至多为 $\sqrt[\uparrow ]{u}$ 的 vEB 树上。由于 vEB-TREE-INSERT 操作的剩余部分运行时间为 $O(1)$ ，所以整个运行时间为 $O(\log \log u)$ 。

删除一个元素

下面介绍如何从 vEB 树删除一个元素。过程 vEB-TREE-DELETE(V, x) 假设 $x$ 是 vEB 树所表示的集合中的一个元素。

vEB-TREE-DELETE(V, x)
	if V.min == V.max // vEB树只包含一个元素
		V.min = NULL
		V.max = NULL
	else if V.u == 2 // elseif, 一棵基础情形的vEB树
		if x == 0
			V.min = 1
		else V.min = 0
		V.max = V.min
	else if x == V.min
			first-cluster = vEB-TREE-MINIMUM(V.summary)
			x = index(first-cluster, vEB-TREE-MINIMUM(V.cluster[ first-cluster ])
			V.min = x
		 vEB-TREE-DELETE(V.cluster[ high(x) ], low(x))
		 if vEB-TREE-MINIMUM(V.cluster[ high(x) ]) == NULL // 簇为空
			vEB-TREE-DELETE(V.summary, high(x))
			if x == V.max
				summary-max = vEB-TREE-MAXIMUM(V.summary)
				if summary-max == NULL
					V.max = V.min
				else V.max = index(summary-max, vEB-TREE-MAXIMUM(V.cluster[ summary-max ]))
		 else if x == V.max // elseif
			V.max = index(high(x), vEB-TREE-MAXIMUM(V.cluster[ high(x) ]))

vEB-TREE-DELETE 过程工作如下。

1. 如果 vEB 树 $V$ 只包含一个元素，那么很容易删除这个元素，如同将一个元素插入一棵空 vEB 树中一样：只要置 $min,max$ 为 NULL 。第 $1\sim 3$ 行处理这种情况。

2. 否则，$V$ 至少有两个元素。第 $4$ 行判断 $V$ 是否为一棵基础情形的 vEB 树，如果是，第 $5\sim 8$ 行置 $min,max$ 为另一个留下的元素。

3. 第 $9\sim 22$ 行假设 $V$ 包含两个或两个以上的元素，并且 $u\ge 4$ 。在这种情况下，必须从一个簇中删除元素。然而从一个簇中删除的元素可能不一定是 $x$ ，这是因为如果 $x$ 等于 $min$ ，当 $x$ 被删除后，簇中的某个元素会成为新的 $min$ ，并且还必须从簇中删除这个元素。如果第 $9$ 行得出正是这种情况，那么第 $10$ 行将变量 $\text{first-cluster}$ 置为「除了 $min$ 外的最小元素所在的簇号」，并且第 $11$ 行赋值 $x$ 为这个簇中最小元素的值。在第 $12$ 行中，这个元素成为新的 $min$ ，由于 $x$ 已经置为它的值，所以这是要从簇中删除的元素。

4. 当执行到第 $13$ 行时，需要从簇中删除 $x$ ，不论 $x$ 是从参数传递而来的，还是 $x$ 是新的 $min$ 元素。第 $13$ 行从簇中删除 $x$ 。第 $14$ 行判断删除后的簇是否变为空，如果是则第 $15$ 行将这个簇号从 $summary$ 中移除。在更新 $summary$ 之后可能还要更新 $max$ 。第 $16$ 行判断是否正在删除 $V$ 中的最大元素，如果是则第 $17$ 行将「编号为最大的非空簇编号」赋值给变量 $\text{summary-max}$（调用 vEB-TREE-MAXIMUM(V.summary) 执行是因为已经在 $V.summary$ 上递归调用了 vEB-TREE-DELETE ，因此有必要的话，$V.summary.max$ 已被更新）。如果所有 $V$ 的簇都为空，那么 $V$ 中剩余的元素只有 $min$ ；第 $18$ 行检查这种情况，第 $19$ 行相应地更新 $max$ 。否则第 $20$ 行把编号最高簇中的最大元素赋值给 $max$（如果这个簇是已删除元素所在的簇，再依靠第 $13$ 行中的递归调用完成簇中的 $max$ 更正 If this cluster is where the element has been deleted, we again rely on the recursive call in line 13 having already corrected that cluster's max attribute ？）。

5. 最后来处理 $x$ 被删除后 $x$ 簇不为空的情况。虽然在这种情况下不需要更新 $summary$ ，但是要更新 $max$ 。第 $21$ 行判断是否为这种情况。如果是，第 $22$ 行更新 $max$（再依靠递归调用来更正 $max$ ）。

现在来说明 vEB-TREE-DELETE 的最坏情况运行时间为 $O(\log \log u)$ 。初看起来，可能认为递归式 $(20.4)$ 不适用，因为 vEB-TREE-DELETE 会进行两次递归调用：一次在第 $13$ 行，另一次在第 $15$ 行。虽然过程可能两次递归调用都执行，但是要看看实际发生了什么。为了第 $15$ 行的递归调用，第 $14$ 行必须确定 $x$ 簇为空。当在第 $13$ 行进行递归调用时，如果 $x$ 是其簇中的唯一元素，此为 $x$ 簇为空的唯一方式。然而如果 $x$ 是其簇中的唯一元素，则递归调用耗费的时间为 $O(1)$ ，因为只执行第 $1\sim 3$ 行。于是有了两个互斥的可能：

• 第 $13$ 行的递归调用占用常数时间。
• 第 $15$ 行的递归调用不会发生。

无论哪种情况，vEB-TREE-DELETE 的运行时间仍可用递归式 $(20.4)$ 表示，因此最坏情况运行时间为 $O(\log \log u)$ 。