常见问题解决技巧：分而治之算法

最新推荐文章于 2025-03-31 13:31:44 发布

新华

最新推荐文章于 2025-03-31 13:31:44 发布

阅读量2k

点赞数 45

分类专栏：数据结构教程文章标签：数据结构

本文链接：https://blog.csdn.net/mzgxinhua/article/details/135396757

版权

数据结构教程专栏收录该内容

61 篇文章

订阅专栏

概述

分而治之是通过将问题分解为更小的部分来解决问题的范例。然后，它结合小解决方案来创建原始问题陈述的完整解决方案。

分而治之算法简介

在解决问题时，最奇特的事情之一是单个问题可能有多种算法方法来解决。

因此，迄今为止，计算机科学领域中存在数千种已知算法，并且始终有可能添加新的算法。

为了以通用且有效的方式理解和研究这些算法，计算机科学家随着时间的推移开发了一些可以将这些算法分组的类别。

算法世界中的一种这样的范例被称为“分而治之”算法。

顾名思义，分治算法方法涉及将给定问题分解为更小的子问题，然后将这些子问题单独解决，然后再次合并到输出解决方案中。

其背后的逻辑是，通常更容易将问题分解为更简单、更小的问题，从而更容易解决，而不是对一个重要的、特别复杂的问题执行一次性解决方案。

虽然上面给出的定义让您对分而治之算法有一个模糊的概念，但我们的目标是通过本文更深入地研究它并建立对该主题的透彻理解，我们将在其中学习分而治之算法是如何进行的工作。

让我们在下一节中看看同样的内容。

分而治之算法如何工作？

正如我们之前所读到的，在遵循分而治之的算法方法时，我们将手头的给定问题分解为较小的子问题，然后单独解决这些子问题，然后将其合并回最终解决方案。

分而治之算法的工作原理是原子性。这里的概念是，研究（并因此解决）问题的最小单元比研究整个问题更容易。

遵循这个原则，在分治算法中，我们不断地将给定的问题划分为更小的问题，直到这些更小的子问题无法再进一步划分。

这个阶段被称为问题的原子状态。然后算法单独求解这些“原子”，最后将所有子问题的解合并为最终的输出解。整个过程可以借助下图来说明：

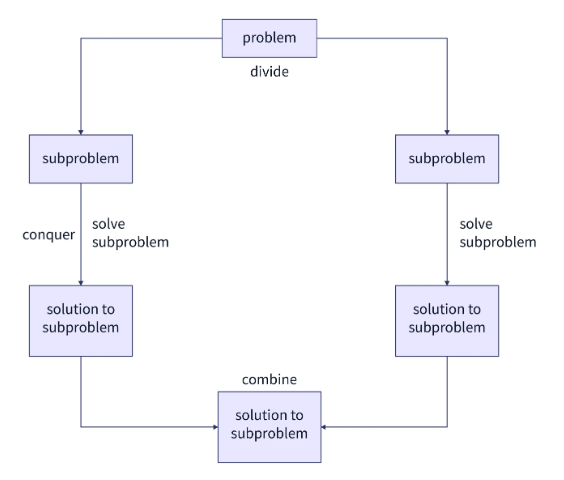
现在让我们看一下分而治之算法的每个阶段，即：

划分：
此步骤将手头的问题划分为更小的原子问题。这里的一个固有规则是这些原子必须代表原始问题，这仅仅意味着这些子问题必须是原始问题的一部分。

分而治之算法的除法部分遵循递归方法来分解问题，直到没有任何子问题可进一步整除。在此步骤之后，算法的输出是原始问题的原子，现在可以对其进行处理以得出解决方案。

征服：
这是分而治之问题解决方法中的中间步骤，理论上，所有单独的原子子问题都得到解决并获得它们的解决方案。但在实践中，通常原始问题在最后阶段（即划分阶段）已经被分解到子问题被视为自行“解决”的水平。
合并：
合并构成了分而治之算法的最后阶段，其中从算法的前一阶段获得的各个解被递归地合并，直到形成原始问题的解。此阶段之后得出的输出是问题所需的解决方案。

从上述步骤的描述可以看出，递归是分而治之算法的核心。无论是将原始问题分解为子问题，还是将各个解决方案合并到最终输出中，这两项任务都是递归完成的。

因此，为了深入理解分而治之的方法，必须很好地理解递归。

现在让我们通过一个例子进一步加深对算法的理解。我们将了解合并排序，这是一种基于分而治之方法的排序算法。

例如，我们将考虑以下未排序的整数数组。

该算法的输出将是一个排序数组，其中的值按升序排列。

正如我们之前所读到的，算法的第一步是将手头的问题划分为原子子问题。在归并排序中，我们不断递归地将初始数组（以及此后的子数组）分成两半，直到子数组不再可整除，即子数组的大小为1。这个过程可以形象化如下：
- 将原始数组分为两部分。
- 将两个子数组进行划分，并进一步划分后续的子数组，直到所有子数组的大小等于 1。
生成的子数组如下。
现在，我们进入算法的征服步骤，根据定义，这些子数组将单独排序。然而，实际上，大小数组不需要任何排序。所以这一步就默认完成了。
最后，我们到达合并排序算法的合并阶段。在这里，我们将以排序的方式递归地组合子数组，直到只剩下一个数组。以下是合并的过程。我们采用两个已排序的子数组，两个子数组的左端都有一个指针。我们不断将最小的值（由两个指针表示）添加到解数组（从而递增指针），直到遍历完两个子数组中的所有元素。下图解释了合并步骤。

合并的工作原理：

最终的数组将是所需的已排序数组。

可以说，由于我们在这一步中一次对两个子数组进行排序和组合，因此也可以说这一步涉及同时运行的分而治之算法的征服和合并阶段。

现在，让我们对合并排序算法进行时间复杂度分析，以了解该方法与冒泡排序、插入排序等其他排序算法相比的效率如何。

正如我们之前讨论的，归并排序主要有三种操作。

除法运算：
除法运算是常数时间运算( O ( 1 ) )无论子数组的大小如何，因为我们只是找到子数组的中间索引(mid=(start+end)/2)然后根据这个中间索引将子数组分为两部分。在整个除法操作期间，我们继续将初始数组在每一层划分为2个子数组，直到得到大小为1的子数组。总共大约有我哦log2n部门运作的级别。
征服操作：
正如我们之前讨论的，将初始数组分解为大小为1的子数组后，这些子数组默认排序。因此，征服操作的时间复杂度为O ( 1 )。
合并操作：
每一级的合并操作，我们一次递归地对2个子数组进行排序和合并，是一个线性时间操作，即O ( n )。正如我们之前讨论的，由于有我哦og2n在划分过程中的级别中，合并步骤平均将花费大约n。log2n脚步。

因此，考虑到所有三种操作，归并排序的结果是氧O ( nlog2n )手术。

将此与插入排序或冒泡排序进行比较，两者的时间复杂度均为二次方O ( n2 )，合并排序被证明是一种相对更快的排序算法，特别是对于大输入大小。

因此，我们了解了分而治之算法在实践中是如何工作的。接下来，让我们将分而治之的方法与动态规划方法来解决问题进行比较。

分而治之与动态规划方法

在解决问题的过程中，分治法和动态规划算法都有一个共同的特点：

在解决之前，初始问题被原子化为更小的子问题，然后以自下而上的方法生成最终输出，其中各个子问题得到解决，并将它们的结果输出合并到最终解决方案中。

然而，这两种算法方法之间的差异只有在原子化或分割步骤之后才变得明显。不同之处在于如何解决子问题并合并到最终解决方案中。

当谈到分而治之的算法时，正如我们之前看到的，子问题被递归地解决和合并，而不是在每个阶段存储单个子问题的结果以供将来参考。

另一方面，动态规划算法存储每个子问题的结果以供将来参考。

这两类算法解决问题的方法的区别源于这些算法在现实场景中的用例。

分治算法通常用作单次解决方案，我们不需要对同一问题或子问题数据进行重新计算。因此，存储各个子问题的密钥只会导致内存资源的浪费。
另一方面，当我们倾向于在未来多次需要解决相同的子问题时，我们使用动态规划算法。因此，保存输出以供将来参考将节省一些计算资源并有助于消除冗余。

让我们举一个例子来帮助我们更好地形象化差异。我们将考虑一个问题，我们想要找到斐波那契数列中的第 n 个斐波那契数。

分而治之算法：

fib(n):
    if n < 2, return n
    else , return fib(n - 1) + fib(n - 2)

上述给出的解决方案基于分而治之的算法方法。对于斐波那契数列中的每个第 n 个斐波那契数，我们不断地将其分解为第( n-1 ）和第( n-2 ）斐波那契数列。这种故障不断递归发生，直到我们到达基本情况（index = 0 或者 n = 1）。到达基本情况后，我们继续解决各个子问题并合并它们的解决方案，直到得到最终解决方案，即第 n 个斐波那契数。下面的推导第四个斐波那契数的例子将帮助我们更好地理解事情。

正如您在上面的解决方案中看到的，我们不存储任何单独的子问题结果。

动态规划算法：

memory = [ ]
fib(n):
    if n in memory: return memory[n]
    else,
        If n < 2, f = n
        else , f = f(n - 1) + f(n - 2)
        memory [n] = f
        return f

在上面给出的解决方案中，我们将每个子问题的结果存储在内存数组中。当我们进一步解决问题时，可以在将来引用和重用这些存储的解决方案。这节省了我们一些重复的计算。

现在我们知道了分而治之算法的工作原理以及它们与动态规划算法有何不同，现在让我们看一下分而治之算法相对于其他类别算法的优势。