次梯度、次梯度下降

 前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家：点击跳转

目录

一，次梯度

1，次梯度、次微分

2，次梯度的性质

3，共轭函数和次梯度

（1）共轭函数和原函数次梯度的对偶

（2）原函数次梯度和共轭函数次梯度的对偶

（3）共轭函数和共轭函数次梯度的对偶

4，近端映射函数和次梯度

（1）近端映射函数和次梯度的对偶

（2）原函数的近端映射函数和共轭函数的近端映射函数的对偶

（3）广义Moreau 分解

二，次梯度下降

三，镜像次梯度下降算法

1，Bregman距离

2，镜像次梯度下降算法

3，实例

---

一，次梯度

1，次梯度、次微分

函数f的次微分：

集合中的每个g都称为次梯度。

2，次梯度的性质

PS：第（2）条的集合加法是A+B={x+y | x in A && y in B} 

（4）凸函数的次梯度是一个非空有界凸集。

（5）某点处的次梯度含有0则代表该点是极值点。

3，共轭函数和次梯度

（1）共轭函数和原函数次梯度的对偶

即的上确界在x处能取到，等价于，y是f在x处的次微分。

（2）原函数次梯度和共轭函数次梯度的对偶

x是共轭函数在y处的次梯度，等价于y是原函数在x处的次梯度。

例子：

例1，f是一元可微函数 

f的次微分是单元素集合{f'}，y是原函数在x处的次梯度即y=f'(x)

根据共轭函数的导数和原函数的导数互为反函数可得，x等于共轭函数的导数在y处的值，

即x是共轭函数在y处的次梯度。

例2，f(x) = |x| 即一阶范数

f的次微分∂f是个分段函数，x<0时∂f={-1}，x=0时∂f=[-1,1], x>0时∂f={1}

f的共轭函数是f*(y)=0, y∈[-1,1]，

f*的次微分∂f*是个分段函数，y=-1时∂f*=(-∞，0],  y∈(-1,1)时，∂f*={0}，y=1时∂f*=[0,+∞)

显然2个次微分完全对应。

应用：

（3）共轭函数和共轭函数次梯度的对偶

    

即的上确界在x处能取到，等价于，x是f*在y处的次微分。

4，近端映射函数和次梯度

（1）近端映射函数和次梯度的对偶

推导：

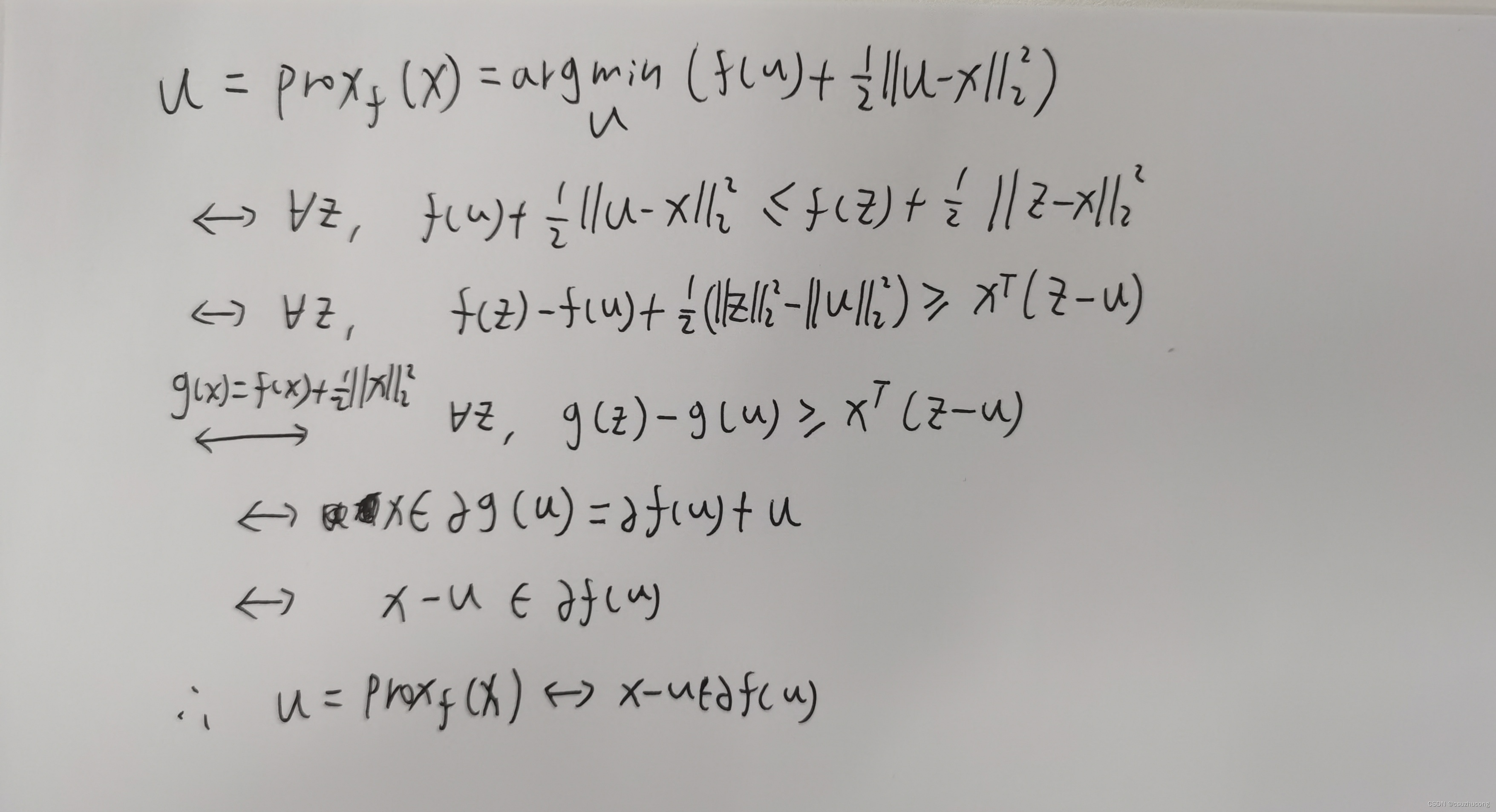
（2）原函数的近端映射函数和共轭函数的近端映射函数的对偶

即Moreau 分解：

推导：

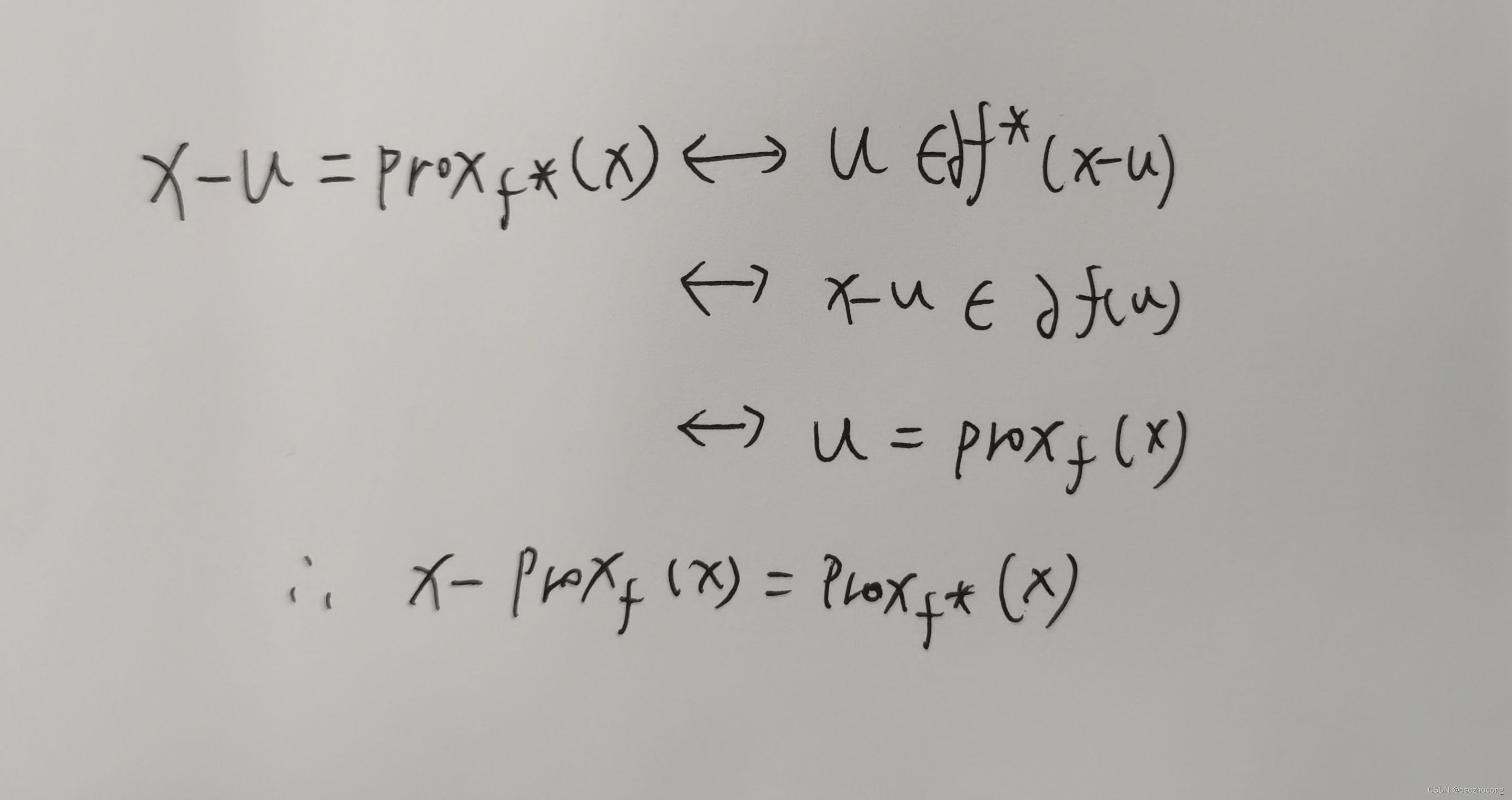
（3）广义Moreau 分解

推导：

二，次梯度下降

在不可微分的场景下，用次梯度取代梯度做梯度下降。 

实际上，各种梯度下降可以对应各种次梯度下降（不一定所有的都能对应）。

比如：

普通梯度下降 对应 普通次梯度下降

投影梯度下降 对应 投影次梯度下降

三，镜像次梯度下降算法

来自这个学习资料

1，Bregman距离

2，镜像次梯度下降算法

迭代求解：

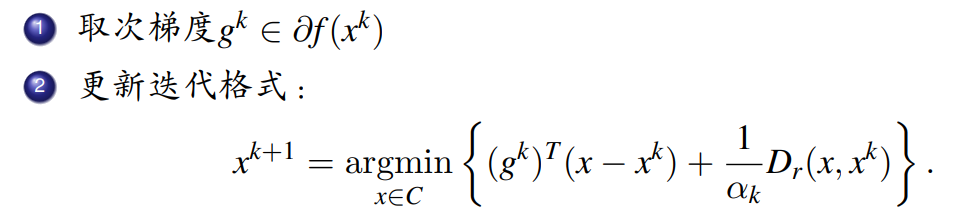
3，实例

比如：

4，收敛条件