高等数学-第七版-上册-第一章函数与极限——第三节 函数的极限

第一章函数与极限——第三节 函数的极限 

*对于没有特殊指明的“总结归纳”，通常指该“总结归纳”的上一张图。

一、函数极限的定义

总结归纳

1.自变量趋于有限值时函数的极限

总结归纳

定义1-函数f(x)当x→x0时的极限

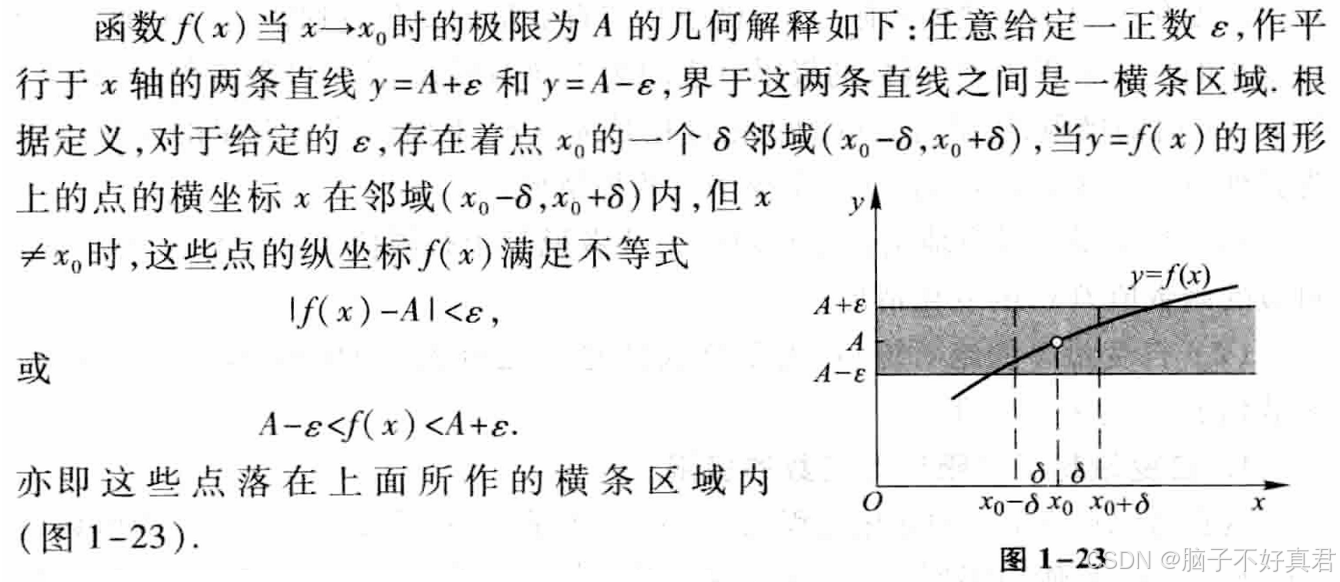
函数f(x)当x→x0时的极限为A的几何解释

例1

例2

例3

例4

例5

例1-例5的方法：ε-δ定义法

左极限与右极限

左极限：x从x0的左侧趋于x0，把 0<|x-x0|<δ 改为 x0-δ<x<x0。
右极限：x从x0的右侧趋于x0，把 0<|x-x0|<δ 改为 x0<x<x0+δ。 

极限存在的充分必要条件

例6

2.自变量趋于无穷大时的函数的极限

小节概述

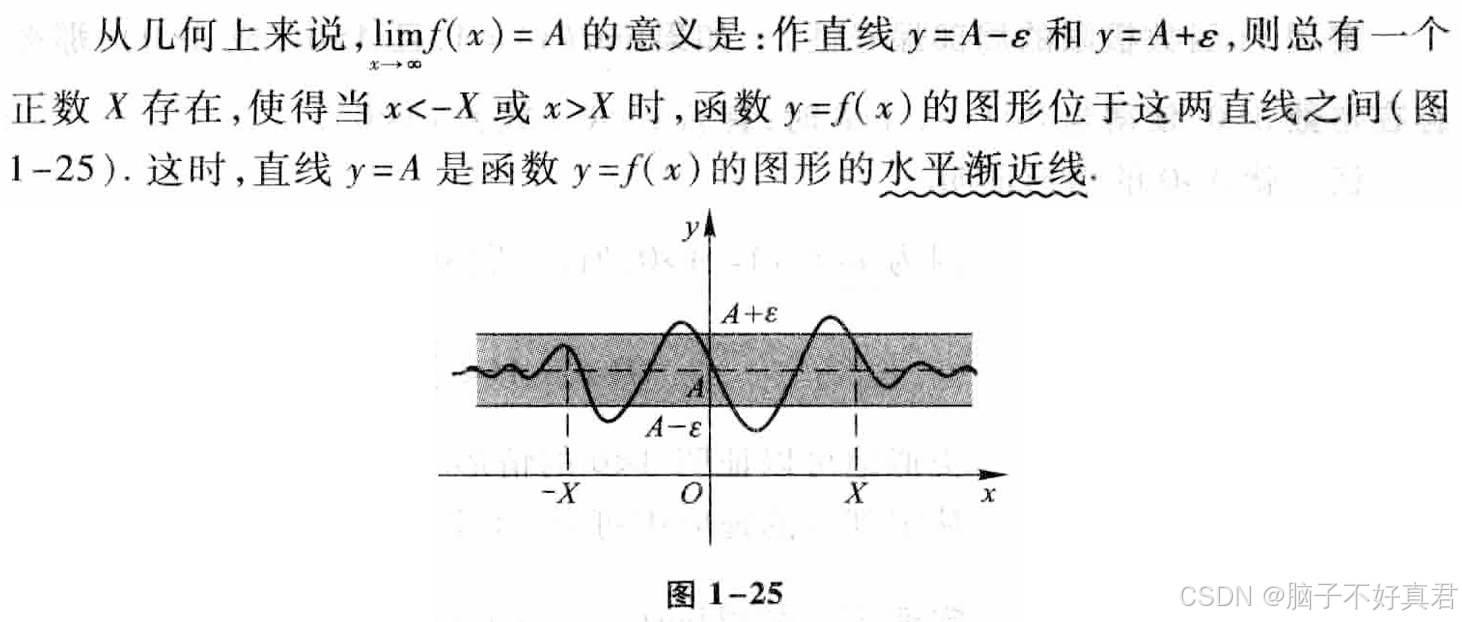
定义2-函数f(x)当x→∞时的极限

函数f(x)当x→x0时的极限为A的几何解释

例7

例7的方法步骤(似ε-δ定义法)

二、函数极限的性质

小节前言

定理1(函数极限的唯一性)

定理2(函数极限的局部有界性)

定理2的证明

定理3(函数极限的局部保号性)

定理3的证明

定理3‘

定理3’的推论

*定理4(函数极限与数列极限的关系)

*定理4的证明

习题1-3

1.

2.

3.

4.

为什么，当 x < 0 时φ(x) = |x|/x = (-x)/x = -1？

*5.

*6.

分清 自变量趋于有限值 和 自变量趋于无穷大 两种情况

*7.

*8.

*9.

*10.

*11.

*12.

参考资料

同济大学数学系. 高等数学 第七版 上册. 高等教育出版社. 2014
同济大学数学系. 高等数学 习题全解指南 第七版 上册. 高等教育出版社. 2014