一篇文章讲清楚同济版高等数学中《第一章——函数与极限》所有求极限的方法

注：本文范围仅限于第一章，所以洛必达法则、泰勒展开法等方法不涉及。

观前提示：一个求函数极限的题目通常涉及的是几种方法的复合，所以有的例题不只是单纯使用的是章节标题的方法，而是复合了其他方法，我想这就是数学难的重要原因之一。

目录

(一)、直接代入法

适用情况：

方法描述：

书中例题：

习题1-9 3 (1)(2)(3)中★(3)提出ln​编辑

习题1-9 4 (1)(2)中★(1)​编辑

(二)、因式分解法

适用情况：

方法描述：

常见的因式分解方法：​编辑

(二.1)、分子分母凑平方差公式

书中例题：

★习题1-9 4 (6)​编辑

★总习题一 9 (2)​编辑

 (二.2)、提取公因式法

方法概述：

书中例题：

★习题1-5 1 (13)，提取公因式n​编辑​编辑

★习题1-9 4 (8)​编辑

(三)、同除法

适用情况：

方法概述：

书中例题：

(五)、倒数函数极限为0⇒原函数极限为∞

方法概述：

书中例题：

★总习题一 9 (1)​编辑

(六)、有界函数与无穷小的乘积是无穷小

方法概述：

书中例题：

(七.1)、两个重要极限——第一重要极限

方法概述：

书中例题：

(七.2)、两个重要极限——第二极限

方法概述：​编辑

书中例题：

(八)、等价无穷小替换

方法概述：

常用等价无穷小：​编辑

书中例题：

(九)、拆分法

方法概述：

书中例题：

★总习题一 9 (3)​编辑

★总习题一 9 (5)​编辑

★总习题一 9 (6)

★(十)、换元法

方法概述：

书中例题：

★习题1-9 4 (7)​编辑

★总习题一 9 (7)​编辑

(0)、公式法

方法概述：

等比数列求和公式

书中例题：

等差数列求和公式

书中例题：

立方差公式

书中例题：

和差化积公式​编辑

书中例题：

参考资料

---

(一)、直接代入法

适用情况：

①x→有限值。②代入后函数有定义。

方法描述：

直接代入法顾名思义，把极限点直接代入函数计算。

书中例题：

习题1-5 1 (1)，直接把2代入x。

习题1-5 1 (2)，直接把根号3代入x。

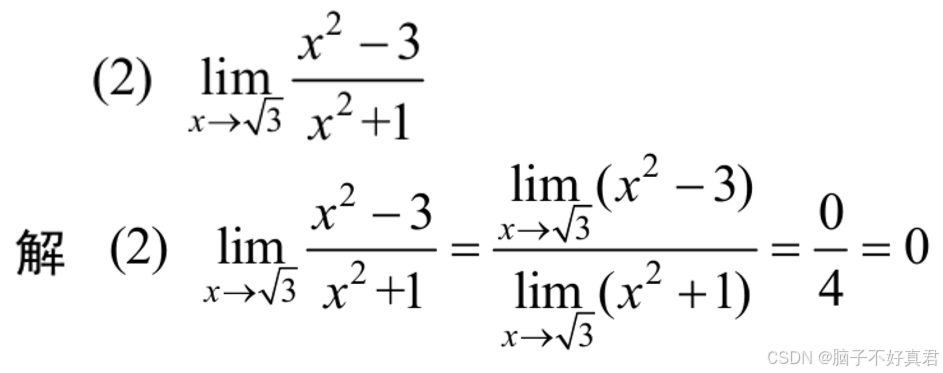
习题1-5 1 (4)，此题不为单独直接代入法，为同除法+直接代入法复合，之后的章节(三)会讲解同除法。

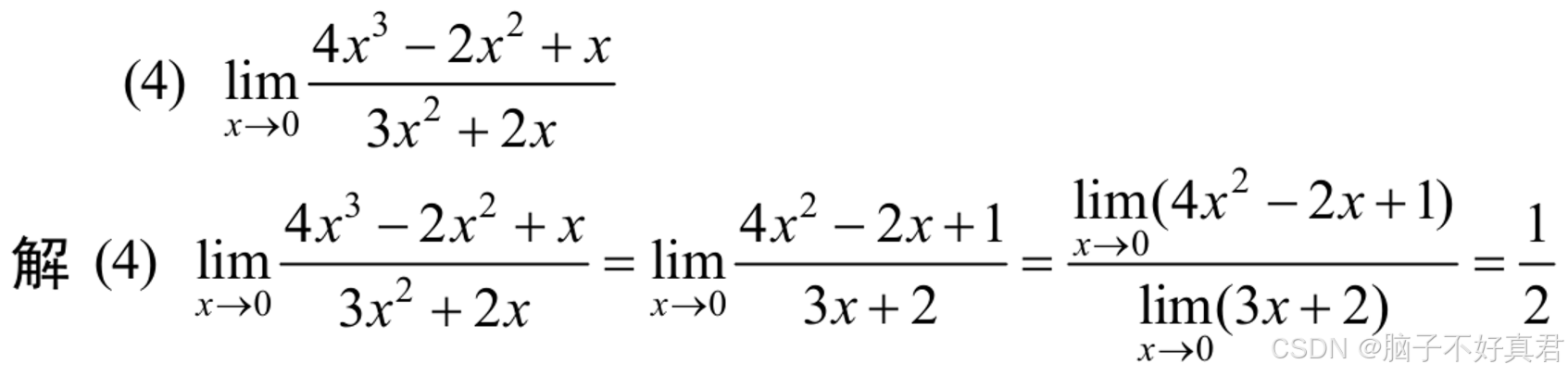
习题1-9 3 (1)(2)(3)中★(3)提出ln

习题1-9 4 (1)(2)中★(1)

(二)、因式分解法

适用情况：

①运用公式进行因式分解。②约分化繁为简。

方法描述：

因式的定义：“因式”（factor）是指能整除某个数学对象（如多项式、整数或矩阵）的元素。简单来说，因式是一个可以将给定对象拆解成乘法形式的部分，通常是该对象的“组成部分”。
因式分解的定义：“因式分解”是将一个多项式或数学表达式拆解成其因子的过程，这些因子可以是更简单的代数表达式。简单来说，因式分解就是将一个复杂的数学表达式表示成若干个乘积的形式，这些乘积的各个因子比原始表达式简单。

常见的因式分解方法：

(二.1)、分子分母凑平方差公式

书中例题：

习题1-5 1 (3)，运用平方差和完全平方差进行因式分解。

之所以从因式分解法从单拎出来分子分母凑平方差公式的方法，因为它在课后习题中~~~多

习题1-9 3 (4)

其实(4)题可以用等价无穷小替换来解答：

习题1-9 3 (7)

★习题1-9 4 (6)

看看word，In fact答案是最后才使用的代入法，我前面就使用了，不知道严谨不严谨：

★总习题一 9 (2)

 (二.2)、提取公因式法

方法概述：

公因式定义：一个多项式中每一项都含有的相同的因式，叫做这个多项式各项的公因式。提取公因式进行约分化简。

书中例题：

★习题1-5 1 (13)，提取公因式n

★习题1-9 4 (8)

(三)、同除法

适用情况：

①分数形式。②x→∞。
注意：x→0是绝对不适用的，因为分母不可为0。

方法概述：

分子分母同除最高次幂。

书中例题：

习题1-5 1 (7)，实则答案先运用了因式分解法再同除最高次幂最后直接代入，也可以像我写的一样直接同除最高次幂。

习题1-5 1 (8)，同除最高次幂再直接代入。

(五)、倒数函数极限为0⇒原函数极限为∞

理论支持：

第四节 无穷大与无穷小 P34

第四节 无穷大与无穷小 P36

方法概述：

所求原函数的倒数函数极限等于0，则原函数的极限等于∞，但该方法总是正确，该方法只有在 f(x) 为单调正函数或单调负函数时才是正确的(区间单调也算)。对于非单调函数，可能不成立。知之为知之不知为不知具体情况我还不明白，不敢定论。
之所以单列出一个方法，是因为书中给出了一道答题全为这种题目，具体题目如下：

书中例题：

习题1-5 2 全部题目

★总习题一 9 (1)

(六)、有界函数与无穷小的乘积是无穷小

方法概述：

正如题目。

书中例题：

习题1-5 3 全部题目

(七.1)、两个重要极限——第一重要极限

方法概述：

注意第一极限及其变形。

书中例题：

习题1-6 1 (1)

习题1-6 1 (3)

其实也不用写为倒数形式，由于其变形形式，如下即可：

(七.2)、两个重要极限——第二重要极限

方法概述：

书中例题：

习题1-6 2 全部题目

(小标题好像丢了...)

习题1-9 4 (4) 

(八)、等价无穷小替换

方法概述：

正如题目所述。

常用等价无穷小：

图片源于：https://baike.baidu.com/item/%E7%AD%89%E4%BB%B7%E6%97%A0%E7%A9%B7%E5%B0%8F/7796020

书中例题：

习题1-6 1 (5)

习题1-6 1 (6)

习题1-9 3 (8)

总习题一 9 (8)

(九)、拆分法

方法概述：

将表达式拆分之后使用两个重要极限或者其他公式进行求极限，实则也可以归类于各个公式中，为什么要单独列出来？因为我总反应不过来。

书中例题：

习题1-9 4 (5)

★总习题一 9 (3)

★总习题一 9 (5)

★总习题一 9 (6)

此题运用的方法就多了：拆分法+第一重要极限+和差化积+二倍角公式

★(十)、换元法

方法概述：

解一些复杂的因式分解问题，常用到换元法，即对结构比较复杂的多项式，若把其中某些部分看成一个整体，用新字母代替(即换元)，则能使复杂的问题简单化，在减少多项式项数,降低多项式结构复杂程度等方面有独到作用 。

书中例题：

★习题1-9 4 (7)

★总习题一 9 (7)

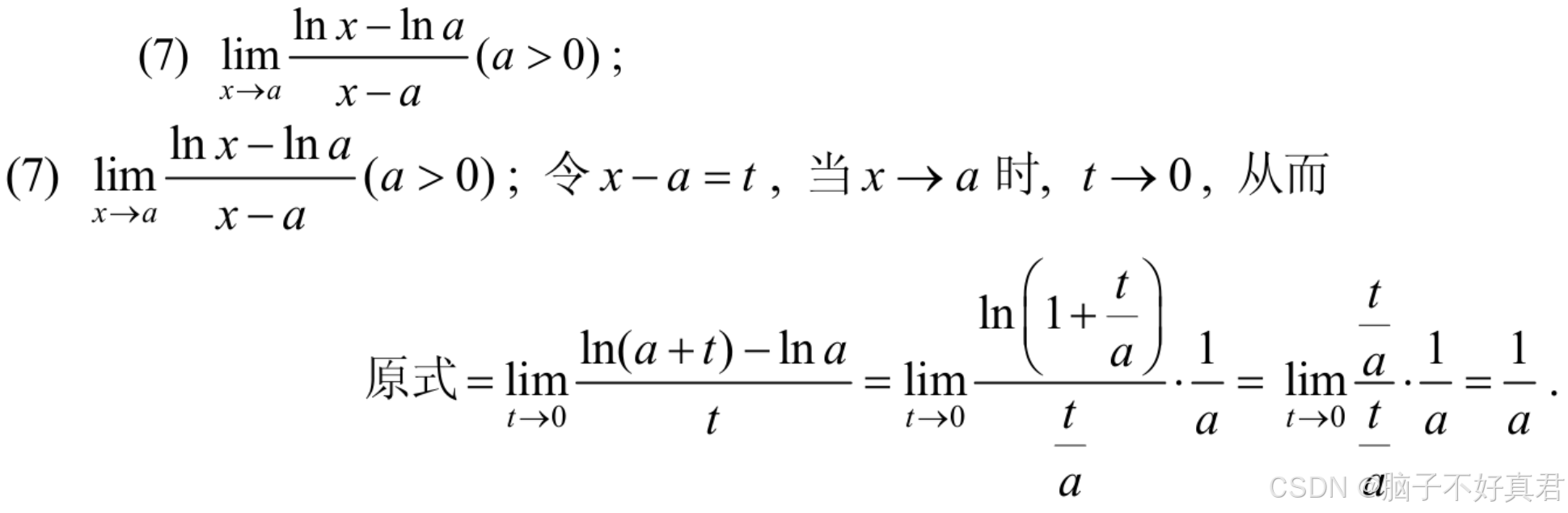
(0)、公式法

方法概述：

之所以不给公式法编号并且放到最后，是因为 "公式法" 这样的说法比较笼统，实际上我们所运用到的大多数方法都是为了约分，化繁为简，但是由于一些具体到公式的解法无法细致归类，我索性就把它们全部归类到 "公式法" 当中。

等比数列求和公式

棋盘格子放麦子，这个故事就源于等比数列，但可以大多数人都没看过故事后半段，很有意思的数学小故事。

书中例题：

习题1-5 1 (11)，运用等比数列求和公式。

等差数列求和公式

数学王子高斯关于等差数列的故事。

书中例题：

习题1-5 1 (12)，运用等差数列求和公式。

立方差公式

书中例题：

习题1-5 1 (14)，运用立方差公式后通分再约分。

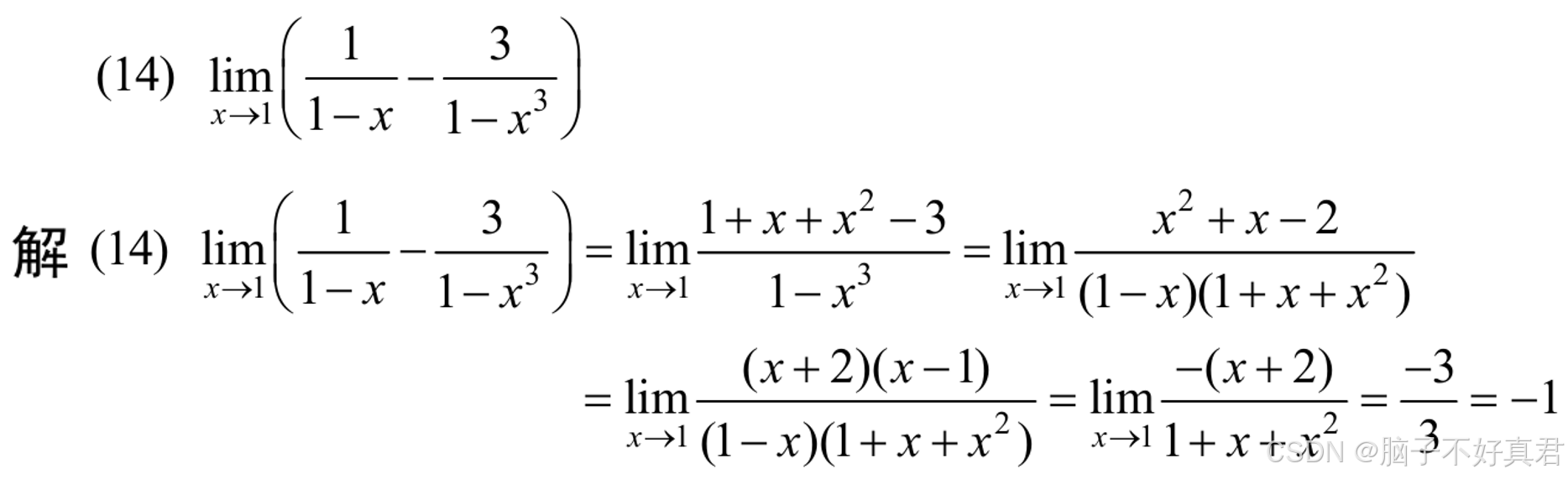
和差化积公式

书中例题：

习题1-9 3 (6)

参考资料

高等数学·上册 第七版 (同济大学数学系)
高等数学 同济第七版 上册 习题辅导书 -- 常桂娟 -- 2015 -- 电子工业出版社
因式分解法_百度百科
等比数列_百度百科
公因式_百度百科
等差数列_百度百科
等价无穷小_百度百科
换元法_百度百科