目录
(0)、理论基础
1. 行列式的性质
性质1 行列式与它的转置行列式相等.
性质2 对换行列式的两行(列),行列式变号.
推论 如果行列式有两行(列)完全相同,则此行列式等于零.
性质3 行列式的某一行(列)中所有的元素都乘同一数 k,等于用数 k 乘此行列式.
推论 行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面.
性质4 行列式中如果有两行(列)元素成比例,则此行列式等于零.
性质5 若行列式的某一行(列)的元素都是两数之和,例如第 i 行的元素都是两数之和,则D等于下列两个行列式之和.
性质6 把行列式的某一行(列)的各元素乘同一数然后加到另一行(列)对应的元素上去,行列式不变.
2. 行列式按行(列)展开定理
(1) 余子式
在n阶行列式中,把(i,j)元 aij 所在的第i行和第j列划去后,留下来的 n-1 阶行列式叫做(i,j)元 aij 的余子式,记作 Mij.
(2) 代数余子式
记Aij = (-1)^(i+j)[这里的(i+j)是指数] * Mij,Aij 叫做(i,j)元 aij 的代数余子式.
引理 一个n阶行列式,如果其中第i行所有元素除(i,j)元 aij 外都为零,那么这行列式等于 ai j与它的代数余子式的乘积,即D = aij * Aij.
定理(行列式按行/列展开法则) 行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积 之和,即
D =ai1Ai1 + ai2Ai2 + … + ainAin (i=1,2,…,n)
D =a1jA1j + a2jA2j + … + anjAnj (j=1 ,2,… ,n)
(一)、 行对换法
题型一
1. 行列式形式(P11 例6):
注意这种题目形式是有规则的,数值排列有章,文字有些乏于描述这种规则,看图吧。
2. 方法概述:
第一轮行交换:第n行与第n-1行交换,第n-1行与第n-2行交换......第2行与第1行交换。
(第一轮一共经过n-1次交换)
第二轮行交换:第n行与第n-1行交换,第n-1行与第n-2行交换......第3行与第2行交换。(此轮交换第1行不动)。
(第二轮一共经过n-2次交换)
第三轮行交换:第n行与第n-1行交换,第n-1行与第n-2行交换......第4行与第3行交换。(此轮交换第1、2行不动)。
(第三轮一共经过n-3次交换)
第四轮行交换:第n行与第n-1行交换,第n-1行与第n-2行交换......第5行与第4行交换。(此轮交换第1、2、3行不动)。
(第四轮一共经过n-4次交换)
依次循环,最终化为上三角行列式。
3. 书中例题:
P11 例6(1)

P11 例6(2)

4.简化版方法概述:

题型二
1. 行列式形式(P15 例11)
行列式数值排列规则,如图。
2. 方法概述:
我选择记结论:

3. 书中例题:
P15 例11
(二)、行列计算法
题型一
1. 行列式形式(P12 例7)
注意这种题目没用规则,数值排列无章。
2. 方法概述:
利用行列式性质2、3、6及其推论关于行和列的三种运算来简化运算,最好可以凑出上三角行列式、下三角行列式、对角行列式的形式。
性质2 对换行列式的两行(列),行列式变号.
推论 如果行列式有两行(列)完全相同,则此行列式等于零.
性质3 行列式的某一行(列)中所有的元素都乘同一数 k,等于用数 k 乘此行列式.
推论 行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面.
性质6 把行列式的某一行(列)的各元素乘同一数然后加到另一行(列)对应的元素上去,行列式不变.
3. 书中例题:
P12 例7
题型二
1. 行列式形式(P12 例8):
注意此题型行列式数值排列有规则:各列元素之和相等,且主对角线元素相同,行列式关于主对角线对称。如下面的一个例子:
2. 方法概述:
把所有元素加到第一行,再用一个数除以第一行把第一行全化为1,最后用第一行减去其余所有行(可以乘以某个数)化为下三角形行列式。
3. 书中例题:
P12 例8
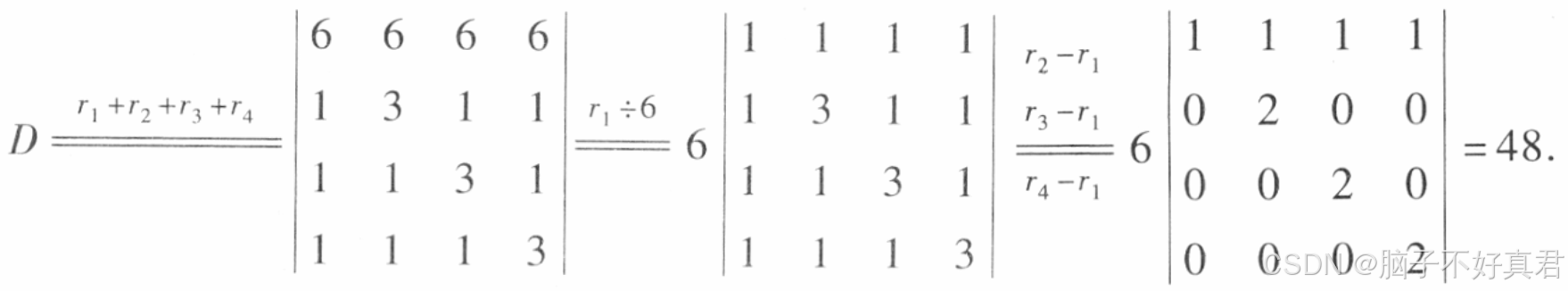
我举一个例子:
题型三
1. 行列式形式(P13 例9)
注意此行列式数值排列规则,特点是第一列元素相同,且可像图中一样用表达式表示。
2. 方法概述:
从第4行开始,后行减前行,但后一次比前一次少一次减法,具体流程如下:
第一轮行减法:第4行减去第3行,第3行减去第2行,第2行前去第1行。
第二轮行减法:第4行减去第3行,第3行减去第2行。
第三轮行减法:第4行减去第3行。
3. 书中例题:
P13 例9

题型四
1. 行列式形式(P14 例10)
数值排列......算有规则吧...
2. 方法概述:

D=D1*D2
3. 书中例题:
P14 例10

书中解答是证明,结论D=D1*D2可直接用。
(三)、行列式行列展开法
题型一
1. 行列式形式(P17 例7续)
注意行列式数值排列无规则。
此题就是P12的例7,不过P12是通过行列计算将行列式化为下三角形来简化的计算,而P17的方法是通过按行列展开来简化计算。
2. 方法概述:
请见 (0)、理论基础 中 行列式按行(列)展开定理。
3. 书中例题:


(四)、范德蒙德行列式
我选择直接记结论,具体证明可看P18。
范德蒙德行列式的计算只看第二行,当然前提是得满足范德蒙德行列式的形式,如图:
举个两个例子加以理解:


参考资料
同济大学数学系. 工程数学 线性代数 第六版. 高等教育出版社. 2014
同济大学数学系. 线性代数 附册学习辅导与习题全解同济 第六版. 高等教育出版社. 2014
范德蒙德行列式_百度百科


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










