算法--简单动态规划(简单dp)

最新推荐文章于 2024-05-19 00:03:09 发布

Tancy.

最新推荐文章于 2024-05-19 00:03:09 发布

阅读量923

点赞数 3

分类专栏：算法文章标签：动态规划算法数据结构 c++ dp

本文链接：https://blog.csdn.net/nefu_TSY/article/details/122827233

版权

算法专栏收录该内容

24 篇文章 5 订阅

订阅专栏

简单dp

概念
状态表示
状态计算
优化
练习题

初级动态规划
算法基础系列

概念

动态规划的理解方式有很多，之前也写过一篇博客，点这里
用的是最优子结构的方法，本篇是另一种方法，状态表示和状态计算方法

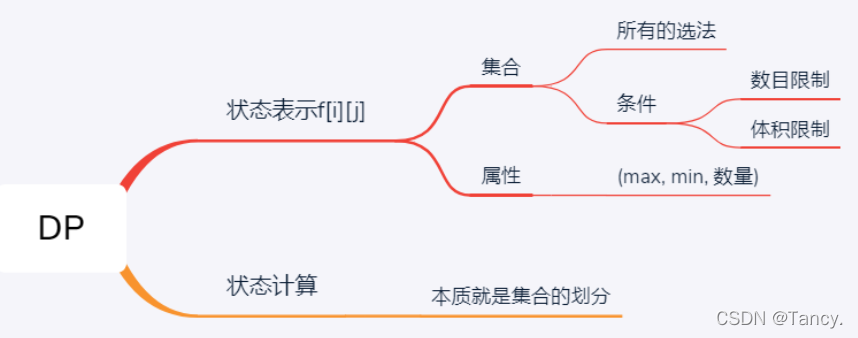
在这里插入图片描述
如图所示
从集合的角度理解
Dp从两个角度考虑

状态表示，考虑清楚用几维表示状态，表示的是哪一个集合，存的数是集合中的哪一个属性
状态计算，如何一步步把每一个状态算出来

状态表示

每一个状态都表示一个集合

因此要考虑，f(i,j) 表示的是哪一个集合，例如背包问题表示的是所有选法的集合

属性：f(i,j) 表示的是一个集合，实际上存的是一个数，这个数是这个集合的某种属性。因此属性一般有三种：max，min，元素数量

集合：表示的是所有选法的一个集合(选哪些物品)
还有满足一些条件，在01背包问题中，条件是从前i个物品选，总体积小于等于题目要求

状态表示举例：在01背包问题中，f(i,j) 表示从前i 个物品中选，总体积小于等于j选法的集合，存的数是这个集合的每一个选法价值的最大值

状态计算

对应的是集合的划分
如何把当前的集合划分为若干个更小的能算出来的子集，能用前面更小的状态(集合)表示出来

划分方式：是否包含(加入)第i 个物品(第i个物品对结果是否有影响)

划分原则：

不重复：某一个元素不可以属于两个集合(不一定满足)
不遗漏：某一个元素不属于任何集合(必须满足)

举例：在01背包问题中
不包含i 的计算：从 0 ~ i-1 中，总体积不超过j选法的集合，因此最大值是f[i-1][j]
包含i的计算：从 0 ~ i 中，总体积不超过j选法，用状态转移方程转换一下，即是：f[i-1][j-vi]+wi 为最大值

总体的最大值是 max(f[i-1][j]+[i-1][j-vi]+wi)

优化

DP的优化一般是对动态规划的代码或是方程做一个等价变形

先写出基本的状态，再做优化

练习题

01背包问题
背包模型题 组合模型
在这里插入图片描述

基本写法，二维数组

#include <bits/stdc++.h>

using namespace std;

const int N = 1005;
int v[N];    // 体积
int w[N];    // 价值
int f[N][N]; // f[i][j], j体积下前i个物品的最大价值
// i 表示第几个物品  j 表示还有多少体积

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            f[i][j] = f[i - 1][j]; //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if (j >= v[i])         // 能装，需进行决策是否选择第i个物品
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;

    return 0;
}

优化版，利用滚动数组+倒序查找
为什么一维情况下枚举背包容量需要逆序？
在二维情况下，状态f[i][j]是由上一轮i - 1的状态得来的，f[i][j]与f[i - 1][j]是独立的。而优化到一维后，如果我们还是正序，则有f[较小体积]更新到f[较大体积]，则有可能本应该用第i-1轮的状态却用的是第i轮的状态。

简单来说，一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」，逆序则不会有这样的问题。

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int v[N]; // 体积
int w[N]; // 价值
int f[N];//N 件物品，背包容量j下的最优解

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)//倒序比较
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    return 0;
}

摘花生
路线模型
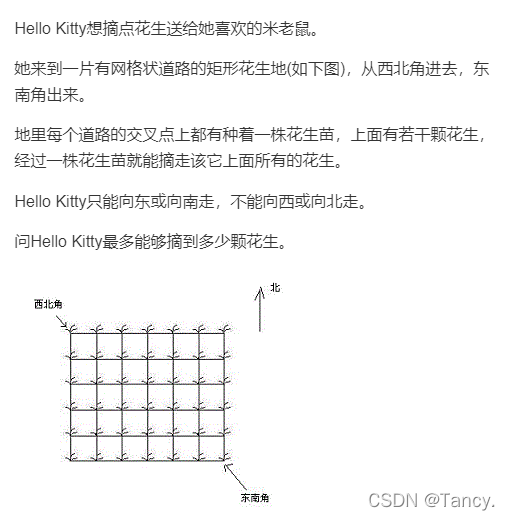
在这里插入图片描述

数字三角形模型

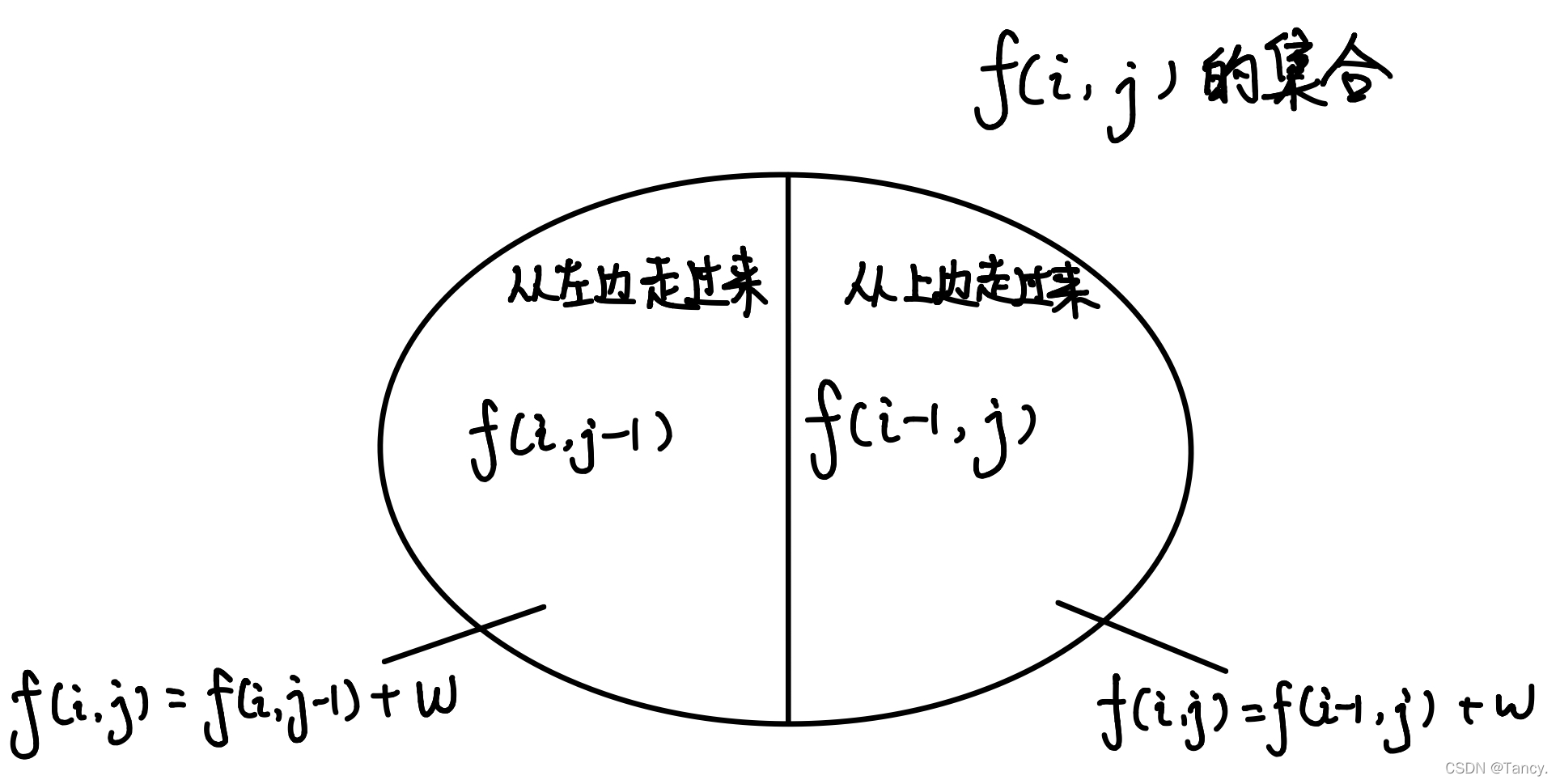
这里只有二维的写法，同理可以用滚动数组优化成一维的

#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int n, m;
int w[N][N];//记录数量
int f[N][N];//记录最优解

int main()
{
    int T;
    cin >> T;
    while (T--)
    {
        cin >> n >> m;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
            {
                cin >> w[i][j];
                f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j]; //两种情况，从上到下或是从左到右
            }
        cout << f[n][m] << endl;
    }
    return 0;
}

最长上升子序列
线性模型
在这里插入图片描述
最长上升子序列模型题

状态表示：f[i]表示从第一个数字开始算，以a[i]结尾的最大的上升序列。(以a[i]结尾的所有上升序列中属性为最大值的那一个)
状态计算（集合划分）:从0 ~ i-1 当 a[i] > a[j] 时，f[i] = max(f[i], f[j] + 1).有一个边界，若前面没有比i小的，f[i]为1（自己为结尾）

时间复杂度是 O(n²)

可以优化到O(nlogn)，用二分优化

朴素写法，双重循环

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int n;
int f[N], a[N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    int res = 0;
    for (int i = 1; i <= n; i++) //求每一个a[i]结尾的最长子序列
    {
        f[i] = 1; //本身的长度为1 (如果没有子序列，自己包含自己)
        for (int j = 1; j < i; j++)
            if (a[j] < a[i]) //是上升的
                f[i] = max(f[i], f[j] + 1);
        res = max(res, f[i]); //找出最长的子序列
    }
    cout << res << endl;
}

地宫取宝
路线模型+线性模型
在这里插入图片描述

思路

四维数组

第一个要想清楚的就是，要取得当前格子的物品，这个物品必须比当前所拥有的物品都大，所以有一个性质：后面拿的物品比前面的物品大

因为价值C的数据是从0到12，而我们一开始不选择的时候f[i][j][u][v],此时v存在不选择的情况所以我们填写比0小的数字-1;
但-1无法做数组下标，因为直接对所有价值全部加1，就变成了1到13

注意特判边界问题

#include <bits/stdc++.h>

using namespace std;

const int N = 55, MOD = 1000000007;

int n, m, k;
int w[N][N];         //价值
int f[N][N][13][14]; // i j k c

int main()
{
    cin >> n >> m >> k;

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            cin >> w[i][j];
            w[i][j]++; //因为c++ 数组不能为-1  所以整体加一
        }

    //特色处理第一个数  选 或 不选 的情况
    f[1][1][1][w[1][1]] = 1; //选择第一个数
    f[1][1][0][0] = 1;       //不选第一个数

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) //两重循环
        {
            if (i == 1 && j == 1) //第一个数已经处理了
                continue;
            for (int u = 0; u <= k; u++)      //处理 k
                for (int v = 0; v <= 13; v++) //处理 c
                {
                    int &val = f[i][j][u][v];
                    val = (val + f[i - 1][j][u][v]) % MOD; //从上往下 不取这个数
                    val = (val + f[i][j - 1][u][v]) % MOD; //从左往右 不取这个数
                    if (u > 0 && v == w[i][j])             //如果取了的总价值 等于c
                        for (int c = 0; c < v; c++)
                        {
                            val = (val + f[i - 1][j][u - 1][c]) % MOD;
                            val = (val + f[i][j - 1][u - 1][c]) % MOD;
                        }
                }
        }

    int res = 0;
    for (int i = 0; i <= 13; i++)//汇总所有方案
        res = (res + f[n][m][k][i]) % MOD;

    cout << res << endl;

    return 0;
}

波动数列
组合问题模型
在这里插入图片描述
思路

在这里插入图片描述

#include <bits/stdc++.h>

using namespace std;

const int N = 1010, MOD = 100000007;

int n, s, a, b;
int f[N][N];//方案数

int get_mod(int a, int b)   // 求a除以b的正余数
{
    return (a % b + b) % b;
}

int main()
{
    cin >> n >> s >> a >> b;
    f[0][0] = 1;
    for (int i = 1; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            f[i][j] = (f[i - 1][get_mod(j - a * (n - i), n)] + f[i - 1][get_mod(j + b * (n - i), n)]) % MOD;

    cout << f[n - 1][get_mod(s, n)] << endl;
    return 0;

}