最大子段和问题
――Neicole (2013.05.19)
0. 问题描述
给定由n个整数组成的序列(a1, a2,…, an),求该序列的子段和的最大值,当所有整数均为负整数时,其最大子段和为0。
1. 三种思想 (组合 + 分治 + 扫描)
1.1 蛮力(组合)思想
1.1.1 说明
这是我们很直接可以想出来的方法,用组合思想去想如何求最大子段和,就是将所有的子段(组合)求出来,然后,在求子段的同时,通过判断每次新求出的子段的是否最大值,进行结果记录。
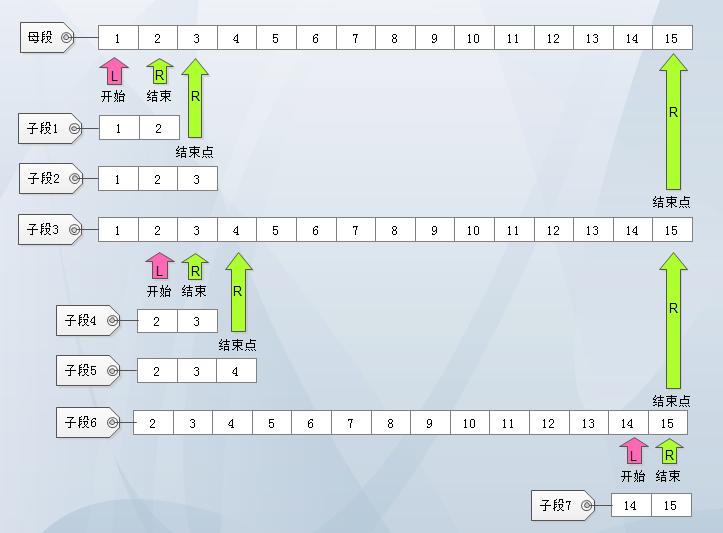
如上图所示,(数字代表数据串里面的第N个数据)如何求出每个子段是该问题的关键,我们可以先设定一个下标L,作为子段的开始位置,再设定一个下标R,作为子段的结束位置,通过固定L,往右移动R,求出当L固定时,以L为起点,以R为结点的子段,直到R到母串的结尾为止。随后,再开始移动子段的开始位置,将下标L依次增大1,每次增大1后,再重复刚刚所讲的运算,固定L,右移R,直至遇上子串末尾,求出当L逐步增大时,以L为起点,以R为结束点的子段,最后,开始点与结束点相遇时,即L等于R时,全部子段即可求出。而在求子段的同时,记录子段的和,通过与每次新子段的比较,得出最大子段和。
由于需要求出n个数的全部组合,所以,该算法的时间复杂度是O(n^2);
1.1.2 伪码
第01步:maxSum = 0
第02步:for L= [startPoint, endPoint)
第03步: for R= (startPoint, endPoint]
第04步: subMaxSum = sum(array[L, R])
第05步: maxSum = max(maxSum, subMaxSum)
第06步:return maxSum;
1.1.3 C++实现
int MaxSum1(int a[], int n)
{
if (n <= 0){
return 0;
}
int sum = 0;
for(int startPoint = 0; startPoint < n; ++startPoint){ // 确定子段的起始坐标
for(int endPoint = n; endPoint > startPoint; --endPoint){ // 确定子段的结束坐标
int tempMaxSum = 0;
++runTimes1;
for(int i = startPoint; i < endPoint; ++i){
tempMaxSum += a[i];
}
if(tempMaxSum >= sum){
sum = tempMaxSum;
}
}
}
if(sum < 0){
sum = 0;
}
return sum;
}
1.2 分治思想
1.2.1 说明
要大小为n的数据,自然地可以将它划分为两段进行处理,每次划分,求出左边子段的最大值,右边子段的最大值,同时跨越两段的子段的最大值,最后结果从这三个最大值中取出最大值即为所求。
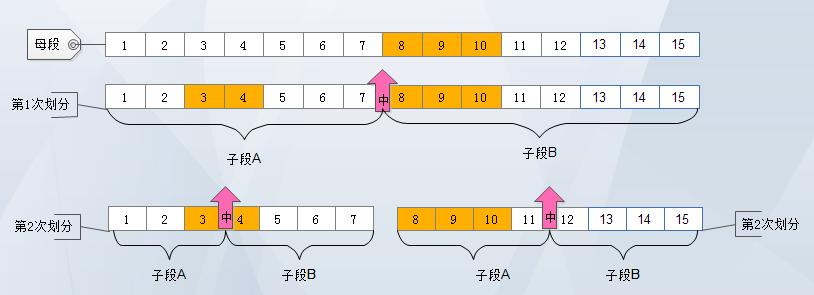
如下图所示,下图将母段两次划分的过程展示出来,其中数字代表下标,带颜色的子段代表在母段中的最大子段和。
第1次划分,以下标7为中点,将母段划分为A、B两段,其中子段A为1-7,子段B为8-15,随后,再进行第2次划分,此时,原子段A再划分,划分出了1-3,4-7两段,当将该子段划分到剩下一个元素时,可以求得这时候的最大子段和在3-4的位置,而在原子段B再划分,划分出了8-11,12-15两段,当将该子段划分到剩下一个元素时,可以求得子段B的最大子段和在8-9的位置,于是,通过这第2次的划分,将划分求值的结果传回到上一次划分当中,由此知道第1次划分时的子段A的最大子段和是1-4,子段B的最大子段和是8-10,最后,再回到母段中,对比子段A和子段B的连续求和的值,求出较大值C1,再求出跨越子段A和子段B的连续子段的和的最大值C2,再由C1和C2取出最大值作为结果。这其中,每次将问题划分为两部分求解,因此此时的算法的时间复杂度为O(log2n),而在求跨段和时,需要再将串遍历一次,因此最后该算法的时间复杂度为O(nlog2n).
1.2.2 伪码
第01步:int MaxSum(int array, int left,int right)
第02步: if left == right
第03步: maxSumRes = max(array[left],0)
第04步: else
第05步: center = (left + right) / 2
第06步: leftSum = MaxSum(array, left, center)
第07步: rightSum = MaxSum(array, center + 1,right)
第08步: endPointWithFuncRight_MaxSum = PartMaxSum(array,left, center)
第09步: startPointWithFuncLeft_MaxSum = PartMaxSum(array,center + 1, right)
第10步: midSum = endPointWithFuncRight_MaxSum + startPointWithFuncLeft_MaxSum
第11步: maxSumRes = max(leftSum, rightSum,midSum)
第12步: return maxSumRes
疑点解释1:第08步,求的是array中从left到center,以center为结束点的子段的和的最大值。
疑点解释2:第09步,求的是array中从center+1到right,以center+1为起点的子段的和的最大值。
疑点解释3:第10步,求的是array中跨越中点的子段的和的最大值。
1.2.3 C++实现
int MaxSum2(int a[], int left, int right)
{
// 范围控制
if(left > right){
return 0;
}
int sum = 0;
if(left == right){ // 序列长度为1,直接求解
sum = (a[left] > 0 ? a[left] : 0 );
}
else{
int center = (left + right) / 2; // 划分
int leftSum = MaxSum2(a, left, center); // 左边最大值
int rightSum = MaxSum2(a, center + 1, right); // 右边最大值
// 跨两边得最值,左边部分
int leftPartSum = 0;
for(int i = center, tempSum = 0; i >= left; --i){
tempSum +=a[i];
++runTimes2;
if(tempSum > leftPartSum){
leftPartSum = tempSum;
}
}
// 跨两边得最值,右边部分
int rightPartSum = 0;
for(int i = center + 1, tempSum = 0; i <= right; ++i){
tempSum += a[i];
++runTimes2;
if(tempSum > rightPartSum){
rightPartSum = tempSum;
}
}
int bothSum = leftPartSum + rightPartSum;
sum = (bothSum > leftSum ? bothSum : leftSum);
sum = (sum > rightSum ? sum : rightSum);
}
return sum;
}
1.3 动态规划(扫描)思想
1.3.1 说明
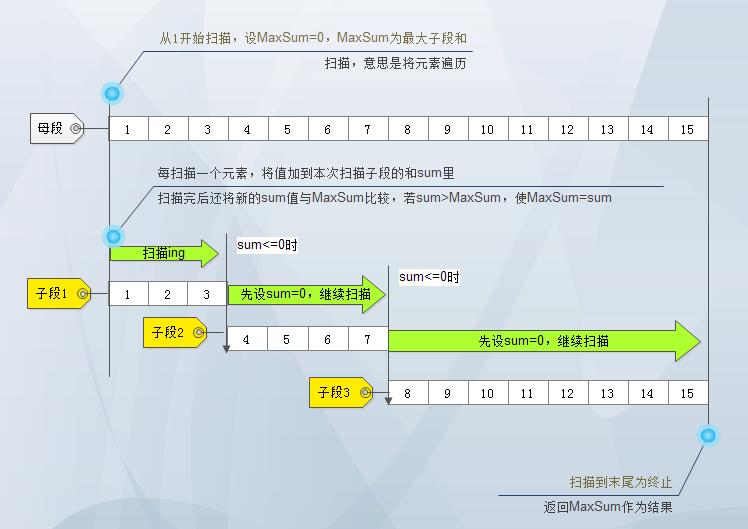
由于它要求的是连续子段和,那么我们可不可以扫描一次数组就将结果求出来呢?可以的,正是因为它是连续的子段。如下图所示:
从母段的下标1开始扫描,设MaxSum=0,MaxSum为最大子段和变量,设sum=0,sum为本次扫描的子段和,开始往右边扫描,每扫描一个元素,将值加到本次扫描子段的和sum中,扫描完单个元素后,将新的sum值与MaxSum进行比较,目标是使MaxSum始终保持最大,当扫描到最后一个元素时,整个算法结束。显然,这算法的时间复杂度为O(n)
理解该算法,关键在于为什么子段可以一直这样扫描下去增加长度,而当sum<=0时,才开始作为新子段,开始新一轮的扫描,这是因为如果为正数时,MaxSum值一直有在做记录,判断一个子段中的最大值是什么,而只有当sum小于0时,我们才需要将sum重新设为零,这是由于结果的最大值必然会大于等于零(题目要求),所以此时可以抛弃前面小于零的子段,重新进行运算。
1.3.2 伪码
第01步:MaxSum = 0
第02步:max = 0
第03步:for i=[0, n)
第04步: max = MAX(max + array[i], 0)
第05步: MaxSum = MAX(max, MaxSum)
第06步:return MaxSum
1.3.3 C++实现
int MaxSum3(int a[], int n)
{
if (n <= 0){
return 0;
}
int sum = 0;
for(int i = 0, tempSum = 0; i < n; ++i){
++runTimes3;
tempSum = (tempSum + a[i] > 0 ? tempSum + a[i] : 0);
if(sum < tempSum){
sum = tempSum;
}
}
return sum;
}
2. 结果
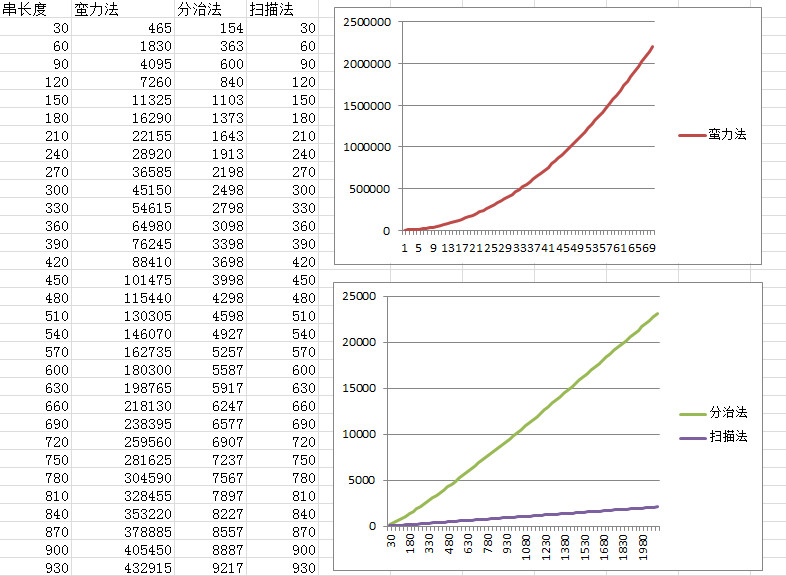
产生长度区间为[30, 2100]的随机串,每个串中的元素的值区间为[-5, 5],分别使用三种算法运算,并计算出基本语句的执行次数,两图中横坐标均为随机串长度,纵坐标为语句执行次数,可以看出,使用蛮力法时,语句执行次数变化曲线接近n的平方,当串长度为30时,语句执行次数为465,当串长度为29时,语句执行次数为1830,使用数据结合算法计算,符合平方差公式。使用分治法时,语句执行次数变化曲线更接近nlog2n,串长度为30时,语句执行次数为154,串长度为60时,语句执行次数为363,符合算法规律。最后是扫描法,串长度与语句执行次数始终保持一致,这是由于算法只需遍历一次母串。
3. 完整代码
/**
* 程序名称:SubsegmentSum
* 问题描述:给定由n个整数组成的序列(a1, a2, …, an),求该序列的子段和的最大值,
* 当所有整数均为负整数时,其最大子段和为0。
* 作者:Neicole
* 时间:2013.05.19
* 联系方式:http://blog.csdn.net/neicole
**/
#include <iostream>
#include <fstream>
#include <cstdlib>
int MaxSum1(int [], int); // 蛮力法求解
int MaxSum2(int [], int, int); // 分治法求解
int MaxSum3(int [], int); // 动态规划法(扫描法)求解
int runTimes1 = 0;
int runTimes2 = 0;
int runTimes3 = 0;
int randInt(int min, int max); // 随机产生一个指定范围内的整数(可正负,但得32位int内的数)
int diffLengthTest(); // 不同长度的随机串的最大连续子串和
int main()
{
// 基本测试
int a[] = {-20, 11, 4, 13, -5, -2};
// 答案为20
int sum1 = MaxSum1(a, sizeof(a)/sizeof(a[0]));
int sum2 = MaxSum2(a, 0, sizeof(a)/sizeof(a[0]));
int sum3 = MaxSum3(a, sizeof(a)/sizeof(a[0]));
std::cout << sum1 << "\t" << sum2 << "\t" << sum3 << "\n";
std::cout << runTimes1 << "\t" << runTimes2 << "\t" << runTimes3 << "\n";
// 随机串测试
std::cout << "\n" << "开始不同长度随机串求子段和测试\n";
diffLengthTest();
system("pause");
return 0;
}
// 不同长度的随机串的最大连续子串和
int diffLengthTest()
{
for(int i = 30; i <= 2100; i+=30){
int * testArr = new int[i]; // 初始化数组
for(int j = 0; j < i; ++j){ // 初始化数组元素
testArr[j] = randInt(-5, 5);
}
runTimes1 = 0;
runTimes2 = 0;
runTimes3 = 0;
MaxSum1(testArr, i);
MaxSum2(testArr, 0, i);
MaxSum3(testArr, i);
std::fstream inFile("testRes.txt", std::ios::app | std::ios::in);
inFile << i << " " << runTimes1 << " " << runTimes2 << " " << runTimes3 << "\n";
inFile.close();
std::cout << i << "\n";
delete [] testArr;
}
return 0;
}
// 随机产生一个指定范围内的整数(可正负,但得32位int内的数)
int randInt(int min, int max)
{
int randIntRes = 0;
if(min > max){
return randIntRes;
}
if(min >= 0){
randIntRes = (rand()+min) % max;
}
// 控制
else{ // (min < 0) // 负数控制
min = 0 - min;
if(max < 0){ // min < max && max < 0
max = 0 - max;
randIntRes = 0 - (rand()+max) % min;
}
else{ // min < max && max >= 0
max += min;
randIntRes = (rand() % max) - min;
}
}
return randIntRes;
}
// 蛮力法
int MaxSum1(int a[], int n)
{
if (n <= 0){
return 0;
}
int sum = 0;
for(int startPoint = 0; startPoint < n; ++startPoint){ // 确定子段的起始坐标
for(int endPoint = n; endPoint > startPoint; --endPoint){ // 确定子段的结束坐标
int tempMaxSum = 0;
++runTimes1;
for(int i = startPoint; i < endPoint; ++i){
tempMaxSum += a[i];
}
if(tempMaxSum >= sum){
sum = tempMaxSum;
}
}
}
if(sum < 0){
sum = 0;
}
return sum;
}
// 分治法
int MaxSum2(int a[], int left, int right)
{
// 范围控制
if(left > right){
return 0;
}
int sum = 0;
if(left == right){ // 序列长度为1,直接求解
sum = (a[left] > 0 ? a[left] : 0 );
}
else{
int center = (left + right) / 2; // 划分
int leftSum = MaxSum2(a, left, center); // 左边最大值
int rightSum = MaxSum2(a, center + 1, right); // 右边最大值
// 跨两边得最值,左边部分
int leftPartSum = 0;
for(int i = center, tempSum = 0; i >= left; --i){
tempSum +=a[i];
++runTimes2;
if(tempSum > leftPartSum){
leftPartSum = tempSum;
}
}
// 跨两边得最值,右边部分
int rightPartSum = 0;
for(int i = center + 1, tempSum = 0; i <= right; ++i){
tempSum += a[i];
++runTimes2;
if(tempSum > rightPartSum){
rightPartSum = tempSum;
}
}
int bothSum = leftPartSum + rightPartSum;
sum = (bothSum > leftSum ? bothSum : leftSum);
sum = (sum > rightSum ? sum : rightSum);
}
return sum;
}
// 动态规划法
int MaxSum3(int a[], int n)
{
if (n <= 0){
return 0;
}
int sum = 0;
for(int i = 0, tempSum = 0; i < n; ++i){
++runTimes3;
tempSum = (tempSum + a[i] > 0 ? tempSum + a[i] : 0);
if(sum < tempSum){
sum = tempSum;
}
}
return sum;
}























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








