基于2D多边形的碰撞检测和响应(四)

四、 基本弧碰撞响应

下面要作的是用给定的量将两个物体分离，并添加一点摩擦和一些静态摩擦，以便使物体静止在斜面上。

该部分使用简单的速度影响算法。同样，为了使碰撞响应更加真实，物体被赋予了质量（更好的是质量的倒数）。

质量的倒数是比较常用的，该值为零意味着该物体具有无穷大的质量，并因此不能移动。同时速度响应中使用质量的倒数具有更好的物理精确性。

现在我们知道多边形A在位置PA具有速度VA，与位置PB速度VB的多边形B发生碰撞。Ncoll和tcoll定义了碰撞平面。如果碰撞前是交叠的，首先分离两个物体，如下：

if (tcoll < 0)
{
    if (A.InvMass == 0)
        PB += Ncoll * tcoll;
    else if (B.InvMass == 0)
        PA -= Ncoll * tcoll;
    else
    {
        PA -= Ncoll * (tcoll * 0.5f );
        PB += Ncoll * (tcoll * 0.5f );
    }
}

然后可以调用碰撞响应的代码，为了简化，我们可以考虑一个粒子碰到一个平面上

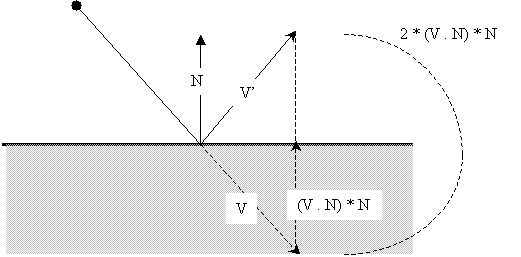
这里V表示粒子的进入速度，V’是粒子发生碰撞后的速度，N为平面的法向。

V’ = V – (2 * (V . N)) * N

理想状态下，碰撞前后粒子的能量是相同的。但是我们可以给粒子的碰撞加入弹性系数

V’ = V – ((1 + elasticity) * (V . N)) * N

弹性系数的范围为[0，1]如果为零意味着粒子将沿着平面滑动，如果为1，粒子将没有能量损耗的弹开。

同样我们可以加入一些摩擦。如果我们沿着碰撞的法线和碰撞平面方向分解速度，我们可以同时计算弹性系数和摩擦力。

这里，速度被沿着平面的法向和平面分解。弹性系数将影响沿着平面法向的响应(Vn)，摩擦力将影响速度的切向（Vt）。

同样摩擦系数的范围为[0，1]. 0意味着没有摩擦力，1意味着粒子将突然停止。

Vn = (V . N) * N;
Vt = V – Vn;
V’ = Vt * (1 – friction) + Vn  * -(elasticity);

对于静摩擦力，简单地在速度Vt小于给定的值时设置Vt为(0,0), 或者设置摩擦系数稍微比1大( 1.001f )。

现在，计算两个物体间的碰撞响应。原理是相同的。然而，计算是基于物体的相对速度的，物体将象上述一样受到影响。结果将添加到每一个物体上。
 

现在我们需要修改一下系数，因为现在我们使用了相对的概念

Vector V = Va – Vb; // relative velocity
Vn = (V . N) * N;
Vt = V – Vn;

if (Vt.Length() < 0.01f ) friction = 1.01f ;

// response
V’ = Vt * -(friction) + Vn  * -(1 + elasticity);

Va += V’ * 0.5f ;
Vb -= V’ * 0.5f ;

这里使物体A和物体B具有相同的响应结果。

为了使结果更加有趣，A和B可以有不同质量。显然较轻的物体会受到较大影响，较重的物体被碰撞影响较小。所以我们可以使用质量来确定两个物体碰撞响应效果。较大的物体具有较小的质量的倒数，如果质量为无穷大质量的倒数为零。

Va += V’ * (InvMassA) / (InvMassA + InvMassB);
Vb -= V’ * (InvMassB) / (InvMassA + InvMassB);