hdu3095

最新推荐文章于 2016-07-22 16:22:39 发布

neuike

最新推荐文章于 2016-07-22 16:22:39 发布

阅读量365

点赞数

分类专栏：搜索

本文链接：https://blog.csdn.net/neuike/article/details/51872808

版权

搜索专栏收录该内容

15 篇文章 0 订阅

订阅专栏

Eleven puzzle

Time Limit: 20000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 616 Accepted Submission(s): 160

Problem Description

Partychen invents a new game named “Eleven Puzzle” .Just like the classic game “Eight Puzzle”,but there some difference between them:The shape of the board is different and there are two empty tiles.

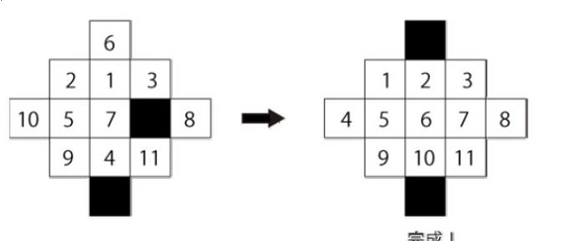
The tile in black means it’s empty

Each step you can move only one tile.
Here comes the problem.How many steps at least it required to done the game.

Input

The first line of input contains one integer specifying the number of test cases to follow.
Every case contains five lines to describe the initial status of the board. 0 means empty.

It’s confirmed that the board is legal.

Output

Output one line for each testcase.Contain an integer denotes the minimum step(s) it need to complete the game.Or “No solution!” if it’s impossible to complete the game within 20 steps.

Sample Input

Sample Output

  
  
   
   2
0
No solution!

Source

2009 Multi-University Training Contest 18 - Host by ECNU

Recommend

lcy

题意：

搜索题。双向bfs，求出起点状态到终点的最小步数。

思路：

双向bfs，每次拓展节点时，从两个空块开始拓展，然后使用一个long long数记录一下当前的状态。

#include<cstring>
#include<string>
#include<iostream>
#include<queue>
#include<cstdio>
#include<algorithm>
#include<map>
#include<cstdlib>
#include<cmath>
#include<vector>
//#pragmp comment(linker, "/STACK:1024000000,1024000000");

using namespace std;

#define INF 0x3f3f3f3f

long long d[30];
int g[5][5];

struct node
{
    int g[5][5];
    int step;
    int x1,y1;
    int x2,y2;
} p;

map<long long,int >mp[2];
queue<node>que;

int dir[][5]= {{0,1},{0,-1},{1,0},{-1,0}};

typedef long long ll;
ll has(int a[][5])
{
    ll sum=0;
    for(int i=0; i<5; i++)
    {
        for(int j=0; j<5; j++)
        {
            if(a[i][j]==0x3f3f3f3f)
                continue;
            else
            {
                if(a[i][j]/10)
                    sum=sum*100+a[i][j];
                else
                    sum=sum*10+a[i][j];

            }
        }

    }
    return sum;
}

inline bool ok(int x1,int y1,node k)
{
    if(x1<0||x1>=5||y1<0||y1>=5)
        return 0;
    if(k.g[x1][y1]==12||k.g[x1][y1]==0x3f3f3f3f)
        return 0;
    else
        return 1;
}
bool inbound(node k,int x,int y)
{
    if(x>=0&&x<5&&y>=0&&y<5)
    {
        if(k.g[x][y]==INF||k.g[x][y]==12) return false;
        else return true;
        return false;
    }
    return false;
}



int dx[]= {0,0,-1,1};
int dy[]= {1,-1,0,0};


void bfs(int flag)
{
//    mp[flag].clear();
//    while(!que.empty())
//        que.pop();
//    mp[flag][has(p.g)]=1;
//    //printf("has:%lld\n",has(p.g));
//    que.push(p);

     mp[flag].clear();
    node k;
    while(!que.empty()) que.pop();
    que.push(p);
    mp[flag][has(p.g)]=1;
    while(!que.empty())
    {
      k=que.front();
        que.pop();
        long long pri=has(k.g);
        if(flag)
        {
            if(mp[0][pri])
            {
                if(k.step+mp[0][pri]-2<=20)
                {
                    printf("%d\n",k.step+mp[0][pri]-2);
                    return ;
                }
                else
                    continue;
            }
        }
        for(int i=0; i<4; i++)
        {
            node ne=k;
            int x,y;
            x=ne.x1=k.x1+dx[i];
            y=ne.y1=k.y1+dy[i];
            //printf("x1:%d  y1:%d   x:%d  y:%d\n",k.x1,k.y1,x,y);
            if(ok(x,y,k))             //!!!!!!!!!!!!!!!!!!!
            {ne.step++;
            if(flag==0&&ne.step>13)
                continue;
            if(flag&&ne.step>11)
                continue;
            swap(ne.g[ne.x1][ne.y1],ne.g[k.x1][k.y1]);
             ll ha=has(ne.g);
            if(mp[flag][ha])
                continue;
            mp[flag][ha]=ne.step;
            ne.x1=x;
            ne.y1=y;
            que.push(ne);
            }
        }
// for(int i=0; i<4; i++)
//        {
//          node ne=k;
//            int x,y;
//            x=ne.x1=k.x1+dir[i][0];
//            y=ne.y1=k.y1+dir[i][1];
//            //printf("x1:%d  y1:%d   x:%d  y:%d\n",k.x1,k.y1,x,y);
//            if(!ok(x,y,k))
//                continue;
//          
//            ne.step++;
//            if(flag==0&&ne.step>13)
//                continue;
//            if(flag&&ne.step>11)
//                continue;
//            swap(ne.g[x][y],ne.g[k.x1][k.y1]);
//             ll ha=has(ne.g);
//            if(mp[flag][ha])
//                continue;
//            mp[flag][ha]=ne.step;
//            ne.x1=x;
//            ne.y1=y;
//            que.push(ne);
//        }

        for(int i=0; i<4; i++)
        {
            int x,y;
            x=k.x2+dx[i];
            y=k.y2+dy[i];
            if(ok(x,y,k))
           //     continue;
            {node ne=k;
            ne.step++;
            swap(ne.g[x][y],ne.g[k.x2][k.y2]);
            if(flag&&ne.step>10)
                continue;
            if(!flag&&ne.step>12)
                continue;
             ll tmp=has(ne.g);
            if(mp[flag][tmp])
                continue;
            ne.x2=x;
            ne.y2=y;
            mp[flag][tmp]=ne.step;
            que.push(ne);
            }
        }
    }
    if(flag)
        puts("No solution!");
}

void bfsx(int flag)
{
    mp[flag].clear();
    node k;
    while(!que.empty()) que.pop();
    que.push(p);
    mp[flag][has(p.g)]=1;
    while(!que.empty())
    {
        k=que.front();
        que.pop();
        long long pri=has(k.g);
         if(flag)
        {
            if(mp[0][pri])
            {
                if(k.step+mp[0][pri]-2<=20)
                {
                    printf("%d\n",k.step+mp[0][pri]-2);
                    return ;
                }
                else
                    continue;
            }
        }

         for(int i=0; i<4; i++)
        {
          node ne=k;
            int x,y;
            x=ne.x1=k.x1+dir[i][0];
            y=ne.y1=k.y1+dir[i][1];
            //printf("x1:%d  y1:%d   x:%d  y:%d\n",k.x1,k.y1,x,y);
            if(!ok(x,y,k))
                continue;
          //  puts("okkkk");
            ne.step++;
            if(flag==0&&ne.step>13)
                continue;
            if(flag&&ne.step>11)
                continue;
            swap(ne.g[x][y],ne.g[k.x1][k.y1]);
             ll ha=has(ne.g);
            if(mp[flag][ha])
                continue;
            mp[flag][ha]=ne.step;
            ne.x1=x;
            ne.y1=y;
            que.push(ne);
        }

             for(int i=0; i<4; i++)
        {
            int x,y;
            x=k.x2+dir[i][0];
            y=k.y2+dir[i][1];
            if(!ok(x,y,k))
                continue;
      node ne=k;
            ne.step++;
            if(flag&&ne.step>11)
                continue;
            if(!flag&&ne.step>13)
                continue;
            swap(ne.g[x][y],ne.g[k.x2][k.y2]);
            ll tmp=has(ne.g);
            if(mp[flag][tmp])
                continue;
            ne.x2=x;
            ne.y2=y;
            mp[flag][tmp]=ne.step;
            que.push(ne);
        }


    }
    if(flag) printf("No solution!\n");
}

int main()
{
    memset(p.g,0x3f3f3f3f,sizeof p.g);
    p.g[0][2]=12;
    p.g[1][1]=1;
    p.g[1][2]=2;
    p.g[1][3]=3;
    p.g[2][0]=4;
    p.g[2][1]=5;
    p.g[2][2]=6;
    p.g[2][3]=7;
    p.g[2][4]=8;
    p.g[3][1]=9;
    p.g[3][2]=10;
    p.g[3][3]=11;
    p.g[4][2]=12;
    p.x1=0;
    p.y1=2;
    p.x2=4;
    p.y2=2;
    p.step=1;

    bfs(0);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        memset(p.g,0x3f3f3f3f,sizeof p.g);
        p.step=1;
        int swi=0;
        for(int i=0; i<5; i++)
        {
            if(i==0||i==4)
            {
                scanf("%d",&p.g[i][2]);
                int j=2;
                if(p.g[i][j]==0)
                {
                    p.g[i][j]=12;
                    if(swi)
                    {
                        p.x1=i;
                        p.y1=j;
                    }
                    else
                    {
                        p.x2=i;
                        p.y2=j;
                    }
                    swi=1;
                }
            }
            else if(i==1||i==3)
                for(int j=1; j<=3; j++)
                {
                    scanf("%d",&p.g[i][j]);
                    if(p.g[i][j]==0)
                    {
                        p.g[i][j]=12;
                        if(swi)
                        {
                            p.x1=i;
                            p.y1=j;
                        }
                        else
                        {
                            p.x2=i;
                            p.y2=j;
                        }
                        swi=1;
                    }
                }
            else
                for(int j=0; j<5; j++)
                {
                    scanf("%d",&p.g[i][j]);
                    if(p.g[i][j]==0)
                    {
                        p.g[i][j]=12;
                        if(swi)
                        {
                            p.x1=i;
                            p.y1=j;
                        }
                        else
                        {
                            p.x2=i;
                            p.y2=j;
                        }
                        swi=1;
                    }
                }
        }
        bfs(1);
    }
    return 0;
}