机器学习中的搜索算法

前言

机器学习中许多问题最终都可归结为一个明确的最优化问题。因此，机器学习中的许多算法不可避免的用到最优化理论中成熟、高效的算法。如之前的文章里介绍的，线性回归与岭回归问题的最优解都有精确的数字解析表达式，因而可以用正规方程算法求解。但是，绝大多数机器学习算法的最优解都没有精确的数学表达式，在这种情况下，需要用到最优化理论中更具一般性的算法。

一、梯度下降算法

梯度下降算法是解决优化问题的重要方法之一，他要求目标函数式可微且无其它约束。思路：假定目标函数可微，算法从空间中任一给定初始点进行指定轮数的搜索，在每一轮搜索中都计算目标函数当前点的梯度，并沿着与梯度相反的方向按照一定步长移动到下一个可行点。
算法如下：

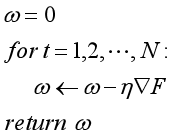
原理：

依据这一原理，可以使用梯度下降算法来实现线性回归：

# 线性回归的梯度优化
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures # 多项式的操作库
class GradLineRegression:
    def fit(self, X, y, eta, N):
        """生成各特征的权重矩阵
        输入：
            X：样本的特征值
            y：样本的标签
            eta：学习率
            N：迭代次数
        返回：
            w：权重值
        """
        m, n = X.shape
        w = np.zeros((n, 1))
        for t in range(N):
            e = X.dot(w) - y
            g = 2 * X.T.dot(e) / m
            w = w - eta * g
        self.w = w
    
    def predict(self, X):
        """样本的预测
        输入：
            X：样本的特征值
        返回：
            无
        """
        return X.dot(self.w)

二、次梯度下降算法

上文介绍到，梯度下降算法要求目标函数可微。在之前的文章中也介绍到Lasso回归得目标函数不可微，在这种情况下便不可使用梯度下降算法。需要一个可以在目标函数不可微得情况下可使用得最优化搜索算法。
首先，次梯度得定义：

几何意义：

而次梯度下降算法为：

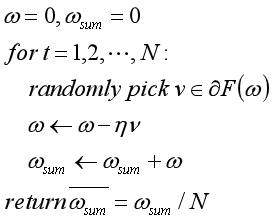
与梯度下降算法相比，次梯度下降算法有如下特征：
1）算法每轮循环中任取一个次梯度的方向作为搜索方向；
2）次梯度下降算法输出所有点的平均值，而不是算法终止时所在的点。这是因为次梯度下降并不能保证每一次循环都严格降低函数值。
接下来利用次梯度算法实现Lasso回归算法。
lasso的目标函数为：

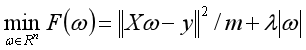
之前的文章已经提过，上式中，前一项为均方误差项，是可微的。后一项为正则化项，不菲处处可微。对于正则化项，一个次梯度为：

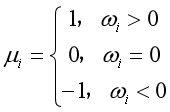
因此，目标函数的一个次梯度为：

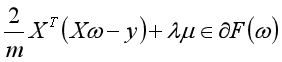
Lasso回归代码的实现：

# lasso回归代码的实现，次梯度算法的应用
class Lasso:
    def __init__(self, Lambda=1):
        self.Lambda = Lambda
    
    def fit(self, X, y, eta=0.1, N=1000):
        """生成各特征的权重矩阵
        输入：
            X：样本的特征值, 
            y：样本的标签值
            eta：学习率
            N：迭代次数
        返回：
            w：权重矩阵
        """
        m, n = X.shape
        w = np.zeros((n,1))
        self.w = w
        for t in range(N):
            e = X.dot(w) - y
            v = 2 * X.T.dot(e) / m + self.Lambda * np.sign(w)
            w = w - eta * v
            self.w += w
        self.w /= N

    def predict(self, X):
        """样本的预测
        输入：
            X：样本的特征值
        返回：
            无
        """
        return X.dot(self.w)

运用上述代码进行实际拟合：

if __name__ == '__main__':
    
    def generate_samples(m):
        X = 2 * (np.random.rand(m,1) - 0.5)
        y = X + np.random.normal(0, 0.3, (m, 1))
        return X, y

    np.random.seed(100)
    X, y = generate_samples(10)
    ploy = PolynomialFeatures(degree=10)
    X_ploy = ploy.fit_transform(X)
    model = Lasso(Lambda=0.01)
    model.fit(X_ploy, y, eta=0.01, N=50000)
    
    plt.axis([-1,1,-2,2])
    plt.scatter(X, y)
    W = np.linspace(-1,1,100).reshape(100,1)
    W_ploy = ploy.fit_transform(W)
    u = model.predict(W_ploy)
    plt.plot(W, u)
    plt.show()

运行结果如下：

显然，使用次梯度下降算法很好的实现了Lasso回归。

三、随机梯度下降算法与小批量梯度下降算法

从上文的描述可以知晓，梯度下降算法每一次迭代都对所有样本数据进行了一次梯度的获取，而当训练数据规模较大时，这是一个非常耗时的计算。
随机梯度下降算法是梯度下降算法的一种改进计算。随机梯度下降算法每次迭代时可以从所有训练数据中取一个采样来估计目标函数梯度，因而它能大幅的降低训练算法的时间复杂度。随机梯度下降算法适用于训练规模较大的场所。
算法如下：

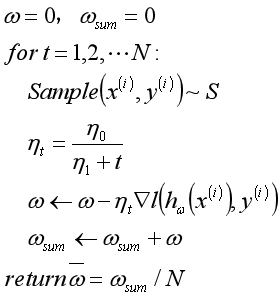
算法中，采用了一个新方法计算学习率。引入了两个参数计算学习率。即随着搜索轮数的增加而减小学习率。
可以使用随机梯度下降算法来实现线性回归，带个数据的梯度为：

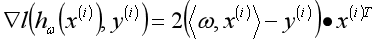
使用代码实现：

# 线性回归随机梯度算法实现
class RandomgradLineRegressionRandom:
    def fit(self, X, y, eta_0=10, eta_1=50, N=3000):
        """生成各特征的权重矩阵
        输入：
            X：样本的特征值, 
            y：样本的标签值
            eta_0, eta_1：算法参数
            N：迭代次数
        返回：
            w：权重矩阵
        """
        m, n = X.shape
        w = np.zeros((n,1))
        self.w = w
        for t in range(N):
            i = np.random.randint(m)
            x = X[i].reshape(1, -1)
            e = x.dot(w) - y[i]
            g = 2 * e * x.T
            w = w - eta_0 * g / (t + eta_1)
            self.w += w
        self.w /= N

    def predict(self, X):
        """样本的预测
        输入：
            X：样本的特征值
        返回：
            无
        """
        return X.dot(self.w)

再二者循环次数相等的情况下，梯度下降算法每次循环时随机梯度下降算法的倍。虽然随机梯度下降算法再时间复杂度上由于梯度下降算法。但是与梯度下降算法相比，其也存在两点不足：
1）训练数据规模较小时，复杂度优势不明显，稳定性也不如梯度下降算法；
2）收敛所需步数较多。
为了改善以上不足，小批量梯度下降算法被提出。即选取固定数量的数据进行梯度下降算法。
其算法表述如下：

采用小批量梯度下降算法实现线性回归：

# 线性回归算法小批次梯度下降算法
class MinbatchGradeLineRegression:
    def fit(self, X, y, eta_0=10, eta_1=50, N=3000, B=10):
        """生成各特征的权重矩阵
        输入：
            X：样本的特征值, 
            y：样本的标签值
            eta_0, eta_1：算法参数
            N：迭代次数
            B：批次的数据量
        返回：
            w：权重矩阵
        """
        m, n = X.shape
        w = np.zeros((n,1))
        self.w = w
        for t in range(N):
            batch = np.random.randint(low=0, high=m, size=B)
            X_batch = X[batch].reshape(B,-1)
            y_batch = y[batch].reshape(B,-1)
            e = X_batch.dot(w) - y_batch
            g = 2 * X_batch.T.dot(e)/B
            w = w - eta_0 * g / (t + eta_1)
            self.w += w
        self.w /= N

    def predict(self, X):
        """样本的预测
        输入：
            X：样本的特征值
        返回：
            无
        """
        return X.dot(self.w)

四，牛顿迭代法

牛顿迭代法是经典的优化算法。许多机器学习算法的优化部分都可以用牛顿迭代算法来实现。与梯度下降算法相比，牛顿迭代算法有如下特点：
1）算法的迭代步数较小；
2）需要计算Hwssian方阵，当模型特征数较大时，可能面临这计算时间复杂性的挑战。
牛顿迭代法的原始应用是计算一元函数的零点。即：

其算法表述为：

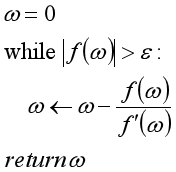
牛顿迭代法的几何意义：如下图所示，牛顿迭代算法迅速收敛到近似零点。在每一步迭代中，计算函数在当前点的切线与横轴的交点并将其作为下一步搜索的点。

由于计算一元函数的最小值可以转化为寻找这个函数导数的零点，所以牛顿迭代算法可以用来求解优化问题。
一元优化问题的牛顿迭代算法表述如下：

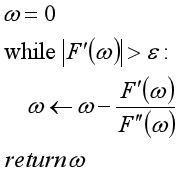
推广到多元函数的牛顿迭代算法表述如下：

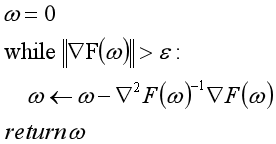
对线性问题而言，如果初始值为0，用牛顿迭代法的解就是正规方程的解。在后续的文章中，会使用牛顿迭代法实现逻辑回归算法。

五，坐标下降算法

坐标下降算法是另一类十分常用的机器学习优化算法。其有两个最为重要且优于梯度下降算法的应用场合：
1）梯度不存在或者梯度函数较为复杂而难于计算。
2）需要求解带约束的优化问题。
坐标下降算法是一个迭代搜索算法。在搜索过程中的每一步，该算法都选取要调整的坐标分量，且固定参数的其它各分量的值。然后沿着选取的分量的坐标轴方向移动到该方向上目标函数值最小的那个点。如此循环使用不同的坐标轴风向，直至沿任何一个坐标轴方向都无法降低目标函数值为止。
基于此，坐标下降算法的表述如下：

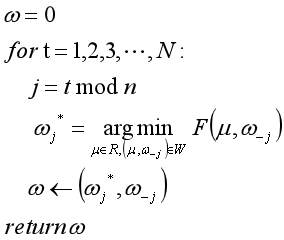
基于此， 利用坐标下降算法实现Lasso回归：

基于此，代码如下：

# Lasso回归坐标下降算法实现
class CoordinateDescentLasso:
    def __init__(self, Lambda):
        self.Lambda = Lambda
    
    def soft_threshold(self, t, x):
        """定义柔和阈值函数
        输入：
            t：柔和阈值
            x：函数变量
        返回：
            柔和阈值函数值
        """
        if x > t:
            return x - t
        elif x >= -t:
            return 0
        else:
            return x + t
    
    def fit(self, X, y, N=1000):
        """生成各特征的权重矩阵
        输入：
            X：样本的特征值, 
            y：样本的标签值
            N：迭代次数
        返回：
            w：权重矩阵
        """
        m, n = X.shape
        alpha = 2 * sum(X**2, axis=0)/m
        w = np.zeros(n)
        for t in range(N):
            j = t % n
            w[j] = 0
            e_j = X.dot(w.reshape(-1, 1)) - y
            beta_j = 2 * X[:, j].dot(e_j) / m
            w[j] = self.soft_threshold(self.Lambda / alpha[j], -beta_j / alpha[j])
        self.w = w

    def predict(self, X):
        """样本的预测
        输入：
            X：样本的特征值
        返回：
            无
        """
        return X.dot(self.w.reshape(-1,1))

思考：根据上述分析，可以发现当正则化系数增大时，权重取0的范围变大，意味着值为0的权重可能变多，符合实际的操作。
那么采用L2正则化的岭回归又如何呢？

总结

本文是《机器学习算法导论》（王磊，王晓东）第四章的学习笔记。