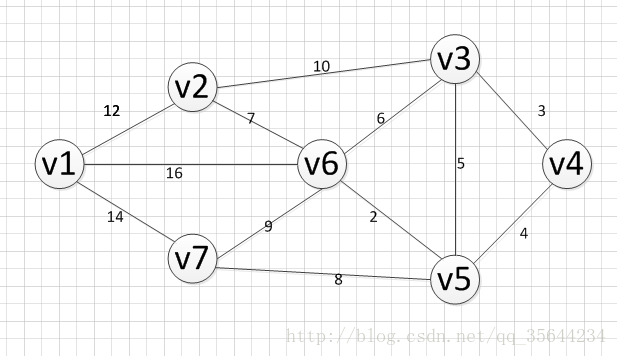
图的最短路径算法——Floyd算法

图的最短路径算法
声明：图源 https://blog.csdn.net/qq_35644234/article/details/60875818
算法代码源 https://www.jianshu.com/p/f910ce1fe7b1
本文主要是代码理解的注解以及调试。。。哇，我觉得代码写的清晰的人真的很厉害啊

Floyd算法

转自：作者：廖少少

链接：https://www.jianshu.com/p/f910ce1fe7b1

来源：简书

简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。

import copy
#定义无穷值
inf=float("inf")
def Floyd(G):
    n=len(G)
    path=copy.deepcopy(G)
    #vi源点,vj目的点,vk作为中间点
    for k in range(0,n):
        for i in range(0,n):
            for j in range(0,n):
                print("Comparing path[%s][%s] and {path[%s][%s]+path[%s][%s]}"%(i,j,i,k,k,j))
                print("Former path[%s][%s]=%s"%(i,j,path[i][j]))
                path[i][j]=min(path[i][k]+path[k][j],path[i][j])
                print("Present path[%s][%s]=%s"%(i,j,path[i][j]))
    return path
if __name__ == "__main__":
    G=[
        [inf,12,inf,inf,inf,16,14],
        [12,inf,10,inf,inf,7,inf],
        [inf,10,inf,3,5,6,inf],
        [inf,inf,3,inf,4,inf,inf],
        [inf,inf,5,4,inf,2,8],
        [16,7,6,inf,2,inf,9],
        [14,inf,inf,inf,8,9