线性回归、逻辑回归的总结

最新推荐文章于 2022-03-10 12:46:34 发布

Nick-Hwong

最新推荐文章于 2022-03-10 12:46:34 发布

阅读量285

点赞数

分类专栏：机器学习

本文链接：https://blog.csdn.net/nickkissbaby_/article/details/89406364

版权

11 篇文章 0 订阅

订阅专栏

广义线性分布（包括线性回归，逻辑回归）首先假设预测变量 $Y$ 服从指数分布族的分布。像线性回归就是假设了 $Y$ 服从了高斯分布。而逻辑回归假设变量服从伯努利分布。
指数分布族的概率密度函数为
$\eta)=b(Y) e^{\left(\eta^{T} T(Y)-a(\eta))\right.}$
其中 $\phi$ 为分布的参数，T(Y)称为充分统计量（一般为Y）

1）线性回归

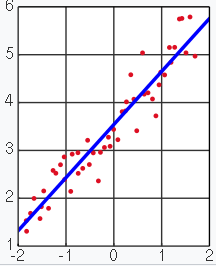
在这里插入图片描述

线性回归可以看成是一种极大似然估计（极大似然估计（MLE）是一种估计参数的方法，MLE假设已经知道随机样本服从的分布但不知道分布的参数，根据当前样本去求使当前样本出现的最大概率的分布参数，即使 $P (W ∣ X)$ 最大）。
我们首先假设Y服从高斯分布 $N(\mu,1)$ ，则Y的概率密度可以转换成指数分布族的一般形式：
$\begin{aligned} P(Y, \eta) &=\frac{1}{\sqrt{2 \pi}} e^{-\frac{(Y-\mu)^{2}}{2}} \\ &=\frac{1}{\sqrt{2 \pi}} e^{-\frac{\gamma^{2}}{2}+\mu Y-\frac{\mu^{2}}{2}} \\ &=\frac{1}{\sqrt{2 \pi}} e^{-\frac{Y^{2}}{2}} e^{\mu Y-\frac{\mu^{2}}{2}} \end{aligned}$
显然， $b(Y)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{Y^{2}}{2}}$ ， $\eta=\mu$ ， $T (Y) = Y$
线性回归假设Y服从分布参数为 $\mu=\eta=\omega^TX$ 的高斯分布 $N(\mu, 1)$ ，则参数W的似然函数为
$\log \prod_{i=1}^{N} \frac{1}{\sqrt{2 \pi}} * e^{-\left(y_{i}-\omega^{T} x_{i}\right)^{2} / 2}$
将似然函数变形，去掉常数项以后得

$\sum_{i=1}^{N}-\left(y_{i}-\omega^{T} x_{i}\right)^{2}$
然后优化问题就可以变为
$\max \sum_{i=1}^{N}-\left(y_{i}-\omega^{T} x_{i}\right)^{2}=\min \sum_{i=1}^{N}\left(y_{i}-\omega^{T} x_{i}\right)^{2}$

Y服从参数为 $\phi$ 的伯努利分布，因此
$P(Y,\phi) = \phi ^ {Y}(1-\phi)^{(1-Y)}=e^{Y\log(\phi)+(1-Y)\log(1-\phi)}=e^{(Y\log(\phi/(1-\phi))+\log(1-\phi))}$
显然， $b (Y) = 1$ , $T (Y) = Y$ ， $\eta=\log(\phi/(1-\phi))$ 。逻辑回归假设分布参数为 $\eta=\omega^TX$ 。可以推导得到
$\phi=\frac{1}{1+e^{-\eta}}$
显然， $\phi(\eta)$ 是一个sigmoid函数。
利用似然估计 $P(Y,\phi)=e^{Y\log(\phi)+(1-Y)\log(1-\phi)}$ 可得
$\log P(Y|\phi)=\log \prod_{i=1}^N(e^{y_i\log(\phi)+(1-y_i)\log(1-\phi)})=\sum_{i=1}^N(y_i\log(\phi)+(1-y_i)\log(1-\phi))$
转成最小化的优化问题得
$\min-\sum_{i=1}^N(y_i\log(\phi)+(1-y_i)\log(1-\phi))$
刚好就是一个分类随处可以见的交叉熵损失函数了…

关注