一般一维数组,称之为向量(vector),
二维数组,称之为矩阵(matrix);
三维数组以及多位数组,我们称之为张量(tensor)。
一、基本概念
矩阵补全(Matrix Completion)目的是为了估计矩阵中缺失的部分(不可观察的部分),可以看做是用矩阵X近似矩阵M,然后用X中的元素作为矩阵M中不可观察部分的元素的估计。
矩阵分解(Matrix Factorization)是指用 A*B 来近似矩阵M,那么 A*B 的元素就可以用于估计M中对应不可见位置的元素值,而A*B可以看做是M的分解,所以称作Matrix Factorization。
这是因为协同过滤本质上是考虑大量用户的偏好信息(协同),来对某一用户的偏好做出预测(过滤),那么当我们把这样的偏好用评分矩阵M表达后,这即等价于用M其他行的已知值(每一行包含一个用户对所有商品的已知评分),来估计并填充某一行的缺失值。若要对所有用户进行预测,便是填充整个矩阵,这是所谓“协同过滤本质是矩阵填充”。
那么,这里的矩阵填充如何来做呢?矩阵分解是一种主流方法。这是因为,协同过滤有一个隐含的重要假设,可简单表述为:如果用户A和用户B同时偏好商品X,那么用户A和用户B对其他商品的偏好性有更大的几率相似。这个假设反映在矩阵M上即是矩阵的低秩。极端情况之一是若所有用户对不同商品的偏好保持一致,那么填充完的M每行应两两相等,即秩为1。
所以这时我们可以对矩阵M进行低秩矩阵分解,用U*V来逼近M,以用于填充——对于用户数为m,商品数为n的情况,M是m*n的矩阵,U是m*r,V是r*n,其中r是人工指定的参数。这里利用M的低秩性,以秩为r的矩阵M’=U*V来近似M,用M’上的元素值来填充M上的缺失值,达到预测效果。
</








 本文介绍了张量的概念,详细讲解了矩阵补全和矩阵分解的基本思想,包括基本矩阵分解方法(Basic mf和Regularized mf)。接着深入探讨了张量的CP分解和Tucker分解,阐述了这两种分解的矩阵形式、计算方法及其应用场景。最后,通过一个数据稀疏性问题展示了张量分解在预测分析中的应用。
本文介绍了张量的概念,详细讲解了矩阵补全和矩阵分解的基本思想,包括基本矩阵分解方法(Basic mf和Regularized mf)。接着深入探讨了张量的CP分解和Tucker分解,阐述了这两种分解的矩阵形式、计算方法及其应用场景。最后,通过一个数据稀疏性问题展示了张量分解在预测分析中的应用。
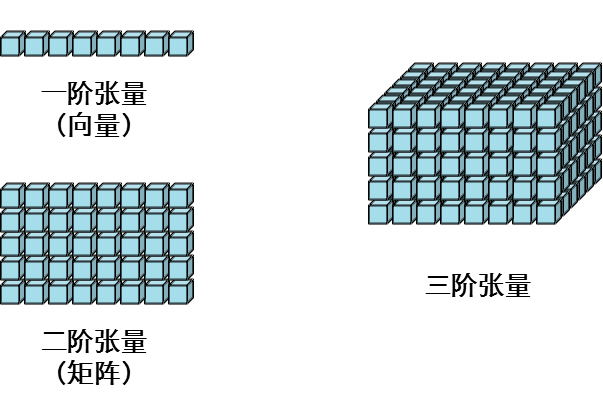
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








