易得最大次为k的概率:k^m/n^m-(k-1)^m/n^m=(k/n)^m-最大值为k-1的概率
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cctype>
#include<ctime>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Lson (x<<1)
#define Rson ((x<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,127,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define INF (2139062143)
#define F (100000007)
#define MAXN (1e5+10)
#define eps (1e-4)
long long mul(long long a,long long b){return (a*b)%F;}
long long add(long long a,long long b){return (a+b)%F;}
long long sub(long long a,long long b){return (a-b+(a-b)/F*F+F)%F;}
typedef long long ll;
int n,m;
double t;
double powe(double a,int b)
{
if (b==1) return a;
if (b==0) return 1;
double t=powe(a,b/2);
t=t*t;
if (b&1) t=t*a;
return t;
}
int main()
{
// freopen("Expected Maximum.in","r",stdin);
// freopen(".out","w",stdout);
scanf("%d%d",&n,&m);
t=1;For(i,m) t/=n;// cout<<t<<endl;
double ans=0,psum=0;
For(k,n)
{
double t=(double)k/(double)n;
t=powe(t,m);
ans+=(t-psum)*k;
psum=t;
}
cout<<ans<<endl;
return 0;
}








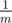 . Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice
. Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice 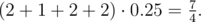














 718
718

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








