代数几何导引（德文版）【瑞士马库斯·布罗德曼（Markus Brodmann）】的读书笔记，翻译和感想（4）

nimo毛毛

已于 2023-10-08 20:45:13 修改

阅读量300

点赞数 1

文章标签：笔记线性代数几何学学习拓扑学矩阵抽象代数

于 2023-10-08 20:42:39 首次发布

本文链接：https://blog.csdn.net/nimomath666/article/details/132937927

版权

前文链接：

代数几何导引（德文版）【瑞士马库斯·布罗德曼（Markus Brodmann）】的读书笔记，翻译和感想（3）_nimo毛毛的博客-CSDN博客Hausdorff, so that换成中文就是：豪斯道夫空间中的两点都属于X，他们是被“邻域”所隔开的，分别是的邻域，意思就是他们的邻域没有任何交集，其交集是空集豪斯道夫空间的定义实际上是通过其性质来定义的空间。其中如果任何两个拓扑可区分的点可以由邻域分离，X是预正则的，有时候也称呼X为空间（预正则空间是空间）给定集合和它的一个子集族，如果满足以下条件，则把称为的拓扑，中的每一个集合都是的开集，并且称为拓扑空间。设为指标集，如果集族，那么；https://blog.csdn.net/nimomath666/article/details/132239032和（3）的知识点补充

代数几何导引（德文版）【瑞士马库斯·布罗德曼（Markus Brodmann）】的读书笔记，翻译和感想（3）-知识点的补充与拓展_nimo毛毛的博客-CSDN博客度量空间也称为距离空间，一种拓扑空间，其上的拓扑由距离决定，设是一个非空集合，是上的二元函数，满足以下条件：1.且2.3.则称为两点之间的距离，按距离成为度量空间或距离空间，记为，设是的子集度量，也就是距离函数，是度量空间中满足特定条件的特殊函数，一般用来表示，度量空间也被称为距离空间，是一类特殊的拓朴空间。详细定义：设为一个非空集合，其元叫做点，是全体实数的集。若函数对于任意满足条件；（a），当且仅当时候成立；（这个就是正定性）（b）；（对称性）https://blog.csdn.net/nimomath666/article/details/132249205我已经托更很久了，我想是时候努力更新了，这一篇是“代数集合”（"Algebraische Menge"）这一章节的最后一部分了，下面我们就要开始"多项式的基本性质"（"Elementare Eigenschaften von Polynomen"），那么我们现在开始吧。

德语原文：

p10

p11

中文翻译：

复数的，实数的，有理的解。连续性原理在实数域内不适用，同样在“复数方法”中不适用。因此我们希望在接下来的文章中仅仅只了解复数解，我们希望接下来仅仅之观察 $X=V(\left \{ f_{i} \right \})\subseteq \mathbb{C}^n$ 的复数解，并且在我们所要观察的多项式需要有被定义好的系数，对此我们我们使用上面引入的写法

$X_\mathbb{R}:=X \cap \mathbb{R}^n,(X\subseteq \mathbb{C}^n)$

并且取 $X_{\mathbb{R}}$ 的实数部分 $X$ 。

类似的我们可以同样通过

$X_{\mathbb{Q}}:=X\cap \mathbb{Q},(X \subseteq \mathbb{C}^n)$

我们现在观察 $X$ 的有理部分

考察有理多项式的有理数解的研究属于实代数几何领域，这些所有的研究不仅仅是关于代数方程组的解集，而是关于代数上的不等式方程组的解集，因此，人们称之为半代数几何，这些理论广泛的使用方法和“经典的”理论不太相同，也就是说复杂代数几何，尽管在处理示例的时候，总是考虑解的实部，因此我们仅限至于复杂/复数理论的描述。

当我们去考虑一个代数集合 $x \subseteq \mathbb{C}^n$ 的有理部分 $X_{\mathbb{Q}}$ 的时候，同样也是非常有意思的，尤其是当被定义的 $X$ 的方程有有理的系数。这些观察方法实际上是属于算术几何领域的并且是和丢番图方程(不定方程)理论紧密联系的，在最后所提到的理论中是算术领域的内容，这是关于整系数代数方程的整数解。

(1.5)例子：一个典型的丢番图方程理论的例子就是毕达哥拉斯三元数，也就是说，对于所有三元数组，都满足

$(i)$ $(u,v,w) \in \mathbb{Z}^3$ ，同时 $u,v,w \neq 0$ 并且 $u^2+v^2=w^2$

当然，我们只对于原始三元数组感兴趣，也就是我们对于互质的三元数组 $(u,v,w)$ 感兴趣

博主注：

原文这里翻译过来应当是“当然，我们只对原始三元数组感兴趣，也就是说，我们对于最大公约数为1的三元数组 $(u,v,w)$ 感兴趣”，在这里我使用了"互质"来代替的“最大公约数为1”

这些三元数组已经从古希腊时期就已经闻名了：

$(ii)$ 原始的毕达哥拉斯三元是由下列集合给出

$\left \{ (2mn,n^2-m^2,n^2+m^2)|n,m \in \mathbb{N}, ggT(n,m)=1,n-m=2k+1,k\in \mathbb{N} \right \}$

博主注“

1. $ggT(n,m)=1$ 的意思是最大公约数为1，ggt是德语”grösst/größt gemeinsamen Teiler“，直接翻译成中文就是“最大的(grösst/größt)，一起的(gemeinsamen)，约数（因子）(Teiler)”

我们现在观察一下复平面上的圆 $X=V(z_{1}^2+z_2^2-1)$ 和集合

$(ii)$ $X_{\mathbb{Q}}=\left \{ (a,b)\in \mathbb{Q}^2 |a^2+b^2 =1\right \}$

的有理点。 $(u,v,w)$ 是一个原始的毕达哥拉斯三元数，所以显然它符合 $(\frac{u}{w},\frac{v}{w})\in X_{\mathbb{Q}}-\left \{ (0,\pm 1),(\pm1,0) \right \}=:\dot{X}_{\mathbb{Q}}$ ，人们这样思考：

$(iii)$ 通过归纳 $(u,v,w) \mapsto (\frac{u}{w},\frac{v}{w})$ 定义了原始毕达哥拉斯三元数集合 $P$ 和不在坐标轴上的圆 $X$ 的有理数集合 $\dot{X_{\mathbb{Q}}}$ 的一个双射

$(1,6)$ 例子：设 $n \in \left \{ 3,4,5,... \right \}$ ，一个数论上的经典问题是所谓的费马问题，也就是说，这个问题是，下列等式

$(i)$ $u^n+v^n=w^n,(n>2)$

是否能够拥有完全非平庸的正整数解 $(u,v,w) \in \mathbb{Z}^3$ （也就是说，解必须要满足条件 $uvw \neq0$ )

坐标轴上的点是否是集合中唯一有理点的问题显然是等价的

$(ii)$ $X_n:=V(z_1^n+z_2^n-1)\subseteq \mathbb{C}^2$

所以 $X_n$ 被称为n次放射费马曲线（翻译未定“？”）

博主注：

翻译未定“？”

原文如下：

"Gleichbedeutend ist offenbar die Frage, ob die Punkte auf den Koordinatenachsen die einzigen rationalen Punkte der Menge

$(ii)$ $X_n:=V(z_1^n+z_2^n-1)\subseteq \mathbb{C}^2$

sind $X_n$ heisst deshalb die n-te affine Fermat-Kurve“

主要问题是不能确定n-te的意思

$(1,7)$ 例子：我们观察代数集合 $X=V(z_1^3+z_2^3-z_1-1 )\subseteq \mathbb{C}^2$ 而且我们对他的实数部分很感兴趣

$(i)$ $X_{\mathbb{Q}}=\left \{ (u,v)\in \mathbb{Q}|u^3+v^2-u-1=0 \right \}.$

显然有

$(ii)$ $(1,\pm 1),(0,\pm 1),(-1,\pm 1)\in X_{\mathbb{Q}}.$

我们可以规定一个纯粹的几何过程（翻译未定“？”），在其中有两个点

$p=(u_0,v_0),q=(u_1,v_1) \in X_{\mathbb{Q}}$

在定义一个点

$<p,q>=(u_2,v_2)\in X_{\mathbb{Q}}$

我们取联络点（翻译未定“？”） $<p,q>$ 为p和q

对此，我们假设 $u_0 \neq u_1$ 并且观察点p和q的连接直线

$L_{p,q}=V((z_1-u_0)\frac{v_1-v_0}{u_1-u_0}-z_2+v_0)$

博主注：

1.翻译未定“？”

原文如下：

”Wir wollen nun einen rein geometrischen Prozess angeben,mit dem wir aus zwei Punkten

                $p=(u_0,v_0),q=(u_1,v_1) \in X_{\mathbb{Q}}$

einen weiteren Punkt

                $<p,q>=(u_2,v_2)\in X_{\mathbb{Q}}$

gewinnen können, den wir den Verbindungspunkt <p,q> von p und q nennen.

Dazu nehmen wir an, es sei $u_0 \neq u_1$ und betrachten die Verbingdungsgerade

                 $L_{p,q}=V((z_1-u_0)\frac{v_1-v_0}{u_1-u_0}-z_2+v_0)$

der Punkte p,q.“

翻译问题所在：

Verbindungspunkt 可以翻译为连接点，也可以翻译为联络点，连接点很好理解，但是联络点涉及到的内容比较多

2.个人认为Verbingdungsgerade就是简单的”连接直线“不是”联络直线“

$X\cap L_{p,q}$ 的割线/切线有以下方程组组成 $z_1^3+z_2^2-z_1-1=0,z_2=(z_1-u_0)\frac{v_1-u_0}{u_1-u_0}+v_0$

对于交点 $(z_1,z_2)\in X \cap L_{p,q}$ 的坐标 $z_1$ ，既满足

$z_1^3+((z_1-u_0)\frac{v_1-v_0}{u_1-u_0}+v_0)^2-z_1-1=0$

由于 $p,q \in X \cap L_{p,q}$ 所以 $z_{1}=u_0,z_1=u_1$ 是方程的解，根据韦达定理，我们可以得到更加进一步的解 $z_1=u_2$ ，我们能给出以下等式

$(iii)$ $u_2=-u_0-u_1-(\frac{v_1-v_0}{u_1-u_0})^2$

相应的，除了点 $p$ 和点 $q$ ， $X \cap L_{p,q}$ 也包含点 $<p,q>$ ，由以下式子给出

$(iv)$ $<p,q>=(u_2,v_2),v_2=(u_2-u_0)\frac{v_1-v_o}{u_1-u_0}+v_0$

这里同样有

$(v)$ $X \cap L_{p,q}=\left \{ p,q,<p,q> \right \}, <p,q> \in \mathbb{Q}^2$

人们同样可以定义点 $p$ 与其自身的连接点 $<p,p>$ ，通过将割线 $l_{p,q}$ 转化成为 $X_{\mathbb{R}}$ 中的切线 $l_{p,q}$ 。人们只不过要在式子 $(iii)$ 和 $(iv)$ 将割线斜率 $\frac{v_1-v_0}{u_1-u_0}$ 替换成为割线斜率 $-\frac{3u_{0}^2-1}{2v_0}$ ：

$(vi)$ $<p,p>=(-2u_0-(\frac{3u_0^2-1}{2v_0})^2,(-3u_0-\frac{3u_0^2-1}{2v_0})^2\frac{3u_0^2-1}{2v_0}+v_0).$

从 $(ii)$ 中的6个点开始，通过不断形成新的连接点，越来越多的新的点在 $X_{\mathbb{Q}}$ 中形成，可以通过一个一定的其他的方式，可以证明 $X_{\mathbb{Q}}$ 的所有的点都可以通过这种方式创建。

$(vii)$ $X_{\mathbb{Q}}$ 最终包含了很多点 $p_1,...p_r$ ，通过继续形成连接点来获得所有的点 $p \in X_{\mathbb{Q}}$

注释：丢番图等式是根据希腊数学家亚历山大·丢番图来命名的，他被认为已经给出了 $(1.5)(ii)$ 中给出的毕达哥拉斯三元数组的处理， $(1.7)$ 中描述的用于产生新有理数解的几何方法也可以追溯到丢番图，同样方法也可以运用到任何具有有理系数的三次方程 $f(z_1,z_3)=0$ ，一般来说会出现 $(1.7)(vii)$ 中所描述的情况（即一旦 $X=V(f)$ 在添加有限数量的点后与环面同胚），即最终有很多点 $p_1,p_2,...,p_r \in X_{\mathbb{Q}}$ ，从中我们可以生成所有的 $p \in X_{\mathbb{Q}}$ ，这是L.S.Mordell（L.S.莫德尔）在1922年在一篇文章中得出的结论，莫德尔定理表达了这样的猜想，对于一般大于三次的方程 $f(z_1,z_2)$ （即他不是无限的，是奇异的（翻译未定“？”）），至多只有有限数量个有理数解。在1983年，G.Faltings在一个更加一般的框架中证明了这个猜想

博主注：

1.翻译未定“？”

原文如下：

(nämlich sobald sie . auch im Unendlichen - nicht singulär ist)

翻译问题所在：

singulär可以翻译为“奇数的”也可以翻译为"奇异的"

丢番图理论的基本上是基于合适素数的解的模的研究，因此，数论的发展也导致了/产生了有限域上的代数几何，同样这个理论在如今发展的非常的好，我们在此就不做过多的赘述。

当然，我们完全可以把丢番图方程的理论看作是“整数 $\mathbb{Z}$ 范围内的代数几何”。同样这个观点也是非常特别的，在代数数论中， $\mathbb{Z}$ 已经被所谓的“整数环”所替代。

读书笔记：

1.半代数

①来自《半代数及其部分结构的刻画》（向长城，魏代俊）的定义

我们之前提到过"半代数几何",先要明白"半代数几何"是什么就要搞清楚什么是"半代数"。在《半代数及其部分结构的刻画》中就有提到关于“半代数”的定义。我将会在这里进行引用

半代数及其部分结构的刻画

半环是人们感到最自然的代数结构之一，因为全体自然数关于通常的加法和乘法就构成一个半环，结合环是半环，因此，半环概念是环概念的一种自然推广，而且许多环论的思想和方法已推广到半环，许多环论的结果都成功地推广到了半环，陈培兹[1],U.Hebsch[5],J.Jezerk[9],Baschir[10],Monico Chris[11]等分别从半环的内部结构如理想，同余及特殊的元素等出发研究半环的结构和特征，而半环的另一研究方法是利用外部环境来讨论，用同调代数的思想和方法来刻画半环的特征.J.S Golan[8],M.Takhashi[15][16][17],Al-Thani H.M.J[12][13]，王永传[14][19]等都在这方面做了大量工作。

本文提出半环上半代数的概念，它同时具有半环结构与半模结构，这一代数结构还没有得到研究。半环上半代数是对谭志松[3],R.S.Pierce[26]中环上代数概念的推广，试图用代数理论和方法来讨论半代数的结构，用半代数的理想，同余，幂等元等概念来讨论N-半单Artin半代数的结构和特征，另一方面试图利用李桃生[4],J.J.Rotman[7]的同调代数的思想和方法来刻画可除半代数和Von Neumann正则半代数，推广了环上模的Baer准则。

$\S 1$ 半代数

半环是介于半群与环之间的代数结构，它是指定义在同一承载集上由分配律联系着的两个群，全体自然数关于数的加法和乘法构成一个半环。

设 $R$ 是一个含有零元和单位元的半环， $(M,+)$ 是一个交换幺半群，若定义一个 $R \times M$ 到 $M$ 的纯量运算， $(r,m) \mapsto rm$ ，并满足：

$(i)(r_1+r_2)m=r_1m+r_2m;$

$(ii)r(m_1+m_2)=rm_1+rm_2;$

$(iii)(r_1r_2)m=r_1(r_2m);$

$(iv)1_rm=m$

$(v)0_rm=0_M=r0_M$ 其中 $r,r_1,r_2 \in R,m,m_1,m_2 \in M$

则称 $M$ 为左- $R$ 半模，记为 $_RM$ ，如果 $M$ 为加法交换群，则 $M$ 作为半环 $R$ 上的左- $R$ 模。

下面我们引入一种新的代数结构，它是环上代数的推广。

定义1.1 一个非空集合 $A$ 称为半环 $R$ 上的半代数，若满足：

$(i)$ A是含有零元和单位元半环 $R$ 上的做 $R$ -半模；

$(ii)$ 在A中定义了一个二元乘法运算 $A \times A \rightarrow A$ 即 $(a,a_1)\mapsto a \cdot a_1$ ，且满足： $a \cdot (a_1+a_2)=a \cdot a_1+a \cdot a_2$ 和 $(a_1+a_2)\cdot a=a_1 \cdot a+ a_2 \cdot a;$

$(iii)r(a \cdot a_1)=(ra) \cdot a_1=a \cdot (ra_1)$ 其中 $\forall r \in R, a,a_1,a_2 \in A$

定义1.2 一个非空集合 $A$ 称为半环 $R$ 上的代数，只需将定义1.1中 $(i)$ 改为 $A$ 是含有零元和单位元半环的左 $R$ -模，(ii)(iii)不变，则称 $A$ 为半环 $R$ 上的代数，显然，这是介于环上代数和半环上半代数的一类代数结构。

由定义可知，半环上半代数是半环上代数的推广，即代数类是半代数，例： $N_0$ 表示全体非负整数， $N_0$ 对于加法和乘法又做成一个含有零元和单位元的半环。显然 $N_0$ 作成自身上的半代数。

与代数，环，半环等概念一样，我们同样可以平行的定义半代数的子半代数，理想等概念

②《代数和半代数互推》的定义

这是一篇从百度文库中翻出来的文章，在本文中阐述代数和半代数的关系，代数和半代数的互推，以及代数和半代数互推在计算机中的作用。

代数和半代数互推

代数和半代数是数学中的两个重要概念，它们在数学中有着广泛的应用。在代数和半代数之间，存在着一种重要的关系，即互推关系。本文将从代数和半代数的定义入手，介绍代数半代数互推的概念和应用。

一、代数和半代数的定义

代数是一种数学结构，它由一组元素和一组运算符组成。这些运算符可以是加、减、乘、除等基本运算符，也可以是更加复杂的运算符，如矩阵乘法、向量积等。代数中的元素可以是数字、向量、矩阵等。

半代数是代数的一种特殊形式，它只包含一个二元运算符，通常表示为" $*$ "。半代数中的元素可以是数字、向量、矩阵等。

二、代数半代数互推的概念

代数和半代数之间存在着一种重要的关系，即互推关系。具体来说，如果一个半代数可以通过某种方式扩展成一个代数，那么这个代数也可以通过某种方式缩减成一个半代数。这种关系被称为代数半代数互推。

代数半代数互推的概念可以通过一个简单的例子来说明。假设有一个半代数，它由元素 $a$ 和 $b$ 以及运算符“ $*$ ”组成，满足以下条件：

$(i)a*a=a$

$(ii)a*b=b$

$(iii)b*b=b$

我们可以通过引入一个新的元素 $c$ 和一个新的运算符“ $+$ ”来将这个半代数扩展成一个代数，具体定义如下：

$a+b=b+a=a$

$b+c=c+b=b$

$a+c=c+a=c$

$a*a=a$

$a*b=b$

$b*b=b$

$a*c=c*a=c$

$b*c=c*b=c$

$c*c=c$

这个代数可以通过缩减运算符“ $+$ ”和元素 $c$ 来得到原来的半代数。

三、代数半代数互推的应用

代数半代数互推在数学中有着广泛的应用。其中一个重要的应用是在计算机科学中，特别是在编译器的设计中。编译器是将高级

语言代码转换成机器语言代码的程序。在编译器中，代数和半代数的概念被广泛应用。

例如，在编译器中，可以使用半代数来表示语法树的节点。语法树是将源代码转换成抽象语法结构的一种数据结构。在语法树中，每个节点都表示一个语法结构，如表达式、语句等。使用半代数来表示语法树的节点可以简化编译器的设计和实现。

另一个重要的应用是在代数几何中。代数几何是一种将代数和几何结合起来研究的数学分支。在代数几何中，代数和半代数的概念被广泛应用。例如，可以使用半代数来表示代数簇的结构。代数簇是一种将代数和几何结合起来研究的数学对象，它可以用半代数来表示。

总之，代数和半代数是数学中的两个重要概念，它们在数学中有着广泛的应用。代数半代数互推是代数和半代数之间的一种重要关系，它在计算机科学和代数几何中有着广泛的应用。

③来自知乎、百度等的整理

对于全集 $\Omega$ 的一个子集类 $A$ ，若 $A$ 是半代数，则 $A$ 满足以下性质

$(i)$ 空集和全集都属于 $A$ ，即 $\varnothing , \Omega \in A$

$(ii)$ $A$ 在有限交运算下封闭，即 $M,N \in A \rightarrow M \cap N \in A$

$(iii)$ 若 $S$ 属于 $A$ ，则 $S$ 的补集也属于 $A$ ，即其补集可以表示成为来自 $A$ 的有限个不相交的元素的并集

博主注：

1.这实际上是在集合代数领域的定义，“即”后面的和前面的内容是等价的，只是转换一种说法或者是用数学语言进行表达

2.子集类，顾名思义，子集的一个类，子集类是由全集的一些子集为“元素”组成的集合

3.运算封闭：若从某个空集合中任意选择2个元素（同一元素可以重新选出）选出的这两个元素通过某种方式（或几种方式）运算后得到的数仍是该数集中的元素，那么该集合对于这种（这几种）运算是封闭的。

        在代数上的定义（代数定义）：

        假设 $S$ 和 $T$ 分别是非空集合， $S$ 上的 $T$ 值运算 $*$ 就是指笛卡尔直积 $S \times S$ 到 $T$ 的一个映射，即

         $*:S \times S \rightarrow T$

        按照传统写法，对于 $S$ 中的2个元素 $a,b$ ，我们用 $a *b$ 来表示这个运算

        当 $S= T$ 的时候，我们就说这个运算是封闭的

4.很显然，能从定义中看出，半代数一定是 $\pi -system$ （ $\pi$ 系），具有“有限交”性质的集系是 $\pi$ 系，即对于非空集合 $P$ 对交封闭，即 $A,B \in P, A \cap B \in P$ ，则我们称呼 $P$ 为 $\pi$ 系或者 $\pi -system$ ，这是属于测度论的内容了，这里不会细讲，我们可能会细讲测度论的内容

2.代数

我们从学数学开始就听说过这些词，“代数式”、“代数”、“代数学”等等等等，再到后来我们就会知道，我们中学所学的是“初等代数”，再到后面就会听说过“高等代数”“线性代数”“抽象代数”等等等，以及我们刚刚提到过的“半代数”和后面可能要提到的“ $\sigma-$ 代数”和“完备 $\sigma-$ 代数”，但是在这之前我想，我们要先弄明白最基础，也是我们最早听到的“代数”一词，那么究竟什么是“代数”呢？

①来自《交换代数导引》（M.F. Atiyah和I.G. Macedonald）的定义

代数

设 $f:A \rightarrow B$ 是环同态，如 $a \in A, b \in B$ ，按公式

$ab=f(a)b$

来定义一个乘积，这个定义就是把环 $B$ 转化成为一个 $A-$ 模（纯量局限的特例），这样一来， $B$ 同时有着一个 $A-$ 模结构和一个环结构，而这两个结构在某种意义上（读者能够子集叙述出来）是协调的，环 $B$ ，附加上这个 $A-$ 模结构之后，就叫做一个 $A-$ 代数，这样一来， $A-$ 代数依定义就是带有一个环同态： $f: A \rightarrow B$ 的环 $B$

注记： $i)$ 如果 $A$ 是域 $K$ （而 $B \neq 0$ ），那么根据 $(1.2)$ , $f$ 是单的，这就是说 $K$ 可以和它在 $B$ 中的象典范地视为同一，因此 $K$ -代数（ $K$ 是域）实质上就是包换 $K$ 作为子集的一个环

$ii)$ 设 $A$ 是任一环，因为 $A$ 有单位元，所以存在着唯一的一个从整数环 $Z$ 到 $A$ 之中的同态 $n \mapsto n \cdot1$ ，所以每个环都自动是一个 $Z$ -代数

设 $f: A \rightarrow B$ 和 $g:A \rightarrow C$ 是两个环同态，一个环同态 $h:B \rightarrow C$ ，如果同时还是 $A$ -模同态，就叫做 $A$ -代数同态，读者应该验证一下， $h$ 是 $A$ -代数同态，当且仅当 $h^{\circ}f=g$

环同态 $f: A \rightarrow B$ 叫做有限的，同时 $B$ 叫做有限的 $A$ -代数，如果 $B$ 作为 $A$ -模是有限生成的，那么同态 $f$ 叫做有限型的，同时 $B$ 叫做有限生成的 $A$ -代数，如果 $B$ 中存在着有限个这样的元素 $x_1,...,x_n$ 使得 $B$ 的每个元素都可以写成 $x_1,...,x_n$ 的系数属于 $f(A)$ 的多项式，等价条件是：存在着从多项式环 $A[t_1,...t_n]$ 到 $B$ 上的 $A$ -代数同态

环 $A$ 叫做有限的，如果它作为 $Z$ -代数是有限生成的，这就是说，在 $A$ 中存在着有限个这样的元素 $x_1,...,x_n$ ，使得 $A$ 的任一元素都可以写成 $x_1,...,x_n$ 的有理系数的多项式。

②来自《代数学》(Thomas W.Hungerford)的定义

博主注：这本书中举了很多例子，在此可能就不会完全引用和抄录，这里只会引用一些典型或者比较简单能够理解的例子

7. 代数

我们在本节里介绍代数及其基本性质，在讨论中大量的使用张量积，在地IX章中还要对代数进一步研究

定义7.1 设 $K$ 是含幺交换环，一个 $K$ -代数（或者叫做 $K$ 上的代数） $A$ 是指具有以下性质的环 $A$

$(i)(A,+)$ 是幺作用（左） $K$ -模；

$(ii)$ $k(ab)=(ka)b=a(kb)$ （对所有 $k \in K , a,b \in A$ ）

一个 $K$ -代数 $A$ 如果是体，便称呼它是除法代数。

代数的经典理论是研究域 $K$ 上的代数，这样的代数是 $K$ 上的向量空间，从而可以用各种线性代数的结果，域 $K$ 上的代数如果作为 $K$ 上的线性空间是有限维的，便称作 $K$ 上有限维代数

定理7.2 设 $K$ 是含幺交换环， $A$ 是幺作用左 $K$ -模。则 $A$ 是 $K$ -代数 $\Leftrightarrow$ 存在 $K$ -模同态 $\pi$ ： $A\bigotimes _KA\rightarrow A$ ，使得图表

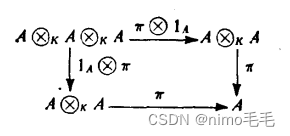
是交换的，在这种情形下， $K$ -代数 $A$ 有幺元素 $\Leftrightarrow$ 存在 $K$ -模同态 $I:K \rightarrow A$ ，使得图表

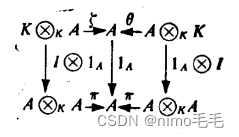
是交换的，其中 $\zeta$ 和 $\theta$ 是定理5.7中的同构。

定义7.3 设 $K$ 是含幺交换群， $A$ 和 $B$ 是 $K$ -代数

$(i)$ $A$ 的子代数是 $A$ 的一个子环并且同时也是 $A$ 的 $K$ -子模

$(ii)$ $A$ 的（左、右或者双侧）代数理想是环 $A$ 的一个（左、右或者双侧）理想，并且同时也是 $A$ 的 $K$ -子模

$(iii)$ $K$ -代数同态（同构） $f:A\rightarrow B$ 是环同态（同构）同时也是 $K$ -模同态（同构）

注记：如果 $A$ 是 $K$ -代数，环 $A$ 的理想不一定是 $A$ 的代数理想（习题4），但是如果 $A$ 有幺元素，则对于每个 $k \in K$ 和 $a \in A$ ，

$ka=k(1_Aa)=(k1_A)a,ka=(ka)1_A=a(k1_A).$

其中 $k1_A \in A$ ，因此对于环 $A$ 的左（右）理想 $J$ ，我们有

$kJ=(k1_A)J\subset J$ $(kJ=J(k1_A)\subset J)$

所以，如果 $A$ 有幺元素，则每个（左、右或者双侧）理想也是（左、右或者双侧）代数理想。

现在可以用显然的方式定义 $K$ -代数 $A$ 对于代数理想 $I$ 的商代数，类似地定义一族 $K$ -代数的直积与直和。

另一种构作新代数的方法是使用张量积，我们首先注意，如果 $A$ 和 $B$ 是 $K$ -模，则有 $K$ -模同构 $a$ : $A\otimes _KB\rightarrow B\otimes_KA$ 使得 $a(a \otimes b)=b\otimes a,(a \in A, b\in B)$

3.数环

什么是环？什么又是数环？我本来打算先写清楚什么是环，在阐述什么是数环，但是看到А.Г.Курош（Α.Γ.库洛什）的《Курс высшей алгебры》（《高等代数教程》）一书中的顺序却是“数环，数域，环，域”，所以我个人也就参考这个顺序来讲解这些。

①来自《Курс высшей алгебры》（《高等代数教程》）的定义

我们曾用“数系”这个名词来表示某一“羣”数，或某些数的“集合”，以后我们要把这个意义非常广泛的数系概念换为比较狭义的名词，它含有和 $Z,R,D$ 和 $K$ 四数系所含有的共同性质，而不同于其他某些数系，例如正整数系和正实数系，至于 $Z,R,D$ 和 $K$ 四个数系，也各有各的性质，例如在 $R,D,K$ 里面可以施行除法（零为除数者除外），就是说在这三种的任何一种数系内，两数相除所得的商仍旧在一个数系里面，但是 $Z$ 里面就没有这种性质，两个整数的商不一定依旧是整数；在 $Z,R$ 和 $D$ 里面的数都有正、负的区别，但是在 $K$ 里面就不能这样划分，诸如此类，另一方面，这四种数系页有他们相同的性质，在他们每一种数系中，对于任何两个数施加加法，乘法以及减法，他们的和，积和差仍然在这种数系里面。

每一种数系，对于它的任何两个数的和、差、积仍旧在它的里面的叫做数环。

博主注：

$Z$ 是整数集合

$R$ 是实数域

$D$ 是有理数域，现在一般是用 $Q$

$K$ 是复数域，现在一般使用 $C$

4.环

之前我们总是提到“环同态”“环”这些概念，我们已经知道了“同态”的概念，那么什么是环呢？这里的“环“指的不是几何上的”环”，而是代数中的“环”。

①来自《近世代数概论》（下册）的定义

$\S 13.1$ 环

在这一章中，我们将着手研究一般的环以及它们的同态，还要指出后者是如何同理想有关，然后我们把理想的概念应用到与代数曲线、代数曲面有关的几何上去，并且应用到与代数曲线、代数曲面有关的几何上去，并且应用到代数数的分解理论中去（第十四章节），我们的基本公设如下所述。

定义环 $A$ 是这样的元素系统，它在加法运算之下是一个阿贝尔群，在乘法运算之下又是封闭的，这个乘法满足结合律，并且对于加法满足分配律，于是，对于环 $A$ 中所有的 $a,b,c$ 有

$a(bc)=(ab)c$

$a(b+c)=ab+ac$ $(1)$

$(a+b)c=ac+bc$

我们还要假定每个环 $A$ 有一个单位元素 $1 \neq 0$ ，满足 $1a=a1=a$ ，对一切 $a \in A$

环包括在第一、二、三章节中所研究的所有整数环和其他交换环，例如 $Z_m$ （模m整数）和 $A[x]$ ， $A[x,y]$ （系数在任一给定的交换环 $A$ 中的多项式环），它还包括非交换环，例如在 $\S 8.11$ 的四元数环，任意给定域 $F$ 上的所有 $n \times n$ 矩阵组成的集合 $M_n(F)$ 在 $A+B$ 和 $AB$ 运算之下都是一个环，当 $n >1$ 时，它也是非交换环。

如果 $A$ 和 $B$ 是任意两个环，那么所有数对 $(a,b)$ （其中 $a \in A, b \in B$ )组成的集合，在由

$(a_1,b_1)+(a_2+b_2)=(a_1+a_2,b_1+b_2),$

$(a_1,b_1)(a_2,b_2)=(a_!a_2,b_1b_2)$

（这两个一起标记成为（2））

定义的两种运算之下是一个换，这样得到的环称为 $A$ 和 $B$ 的直和，记做 $A\oplus B$ ，例如，假设 $\mathbb{Q}$ 是有理数域， $Z$ 是整数环， $Q$ 是四元数环，则 $\mathbb{Q} \oplus Z \oplus Q$ ，这个奇妙的例子对很多类型的环给出了某种表示：

交换环理论的大部分可以推广到非交换环上去。

②来自《近世代数基础》（张禾瑞）的定义

定义一个集合 $R$ 叫做一个环，如果

1. $R$ 是一个加群，换一句话说， $R$ 对于一个叫做假发的代数运算来说作成一个交换群

2. $R$ 对于另一个叫做惩罚的代数运算来说是闭的

3.这个乘法适合结合律

$a(bc)=(ab)c$

不管 $a,b,c$ 是 $R$ 的哪三个元

4.这个乘法适合结合律

$a(b+c)=ab+ac$

$(b+c)a=ba+ca$

不管 $a,b,c$ 是 $R$ 的哪三个元

博主注：

这里有提到关于“加群”的概念，那么什么是加群呢？

定义一个交换群叫做一个加群，假如我们把这个群的代数运算叫做加法，并且用符号 $+$ 来表示

5.数域

①来自《Курс высшей алгебры》（《高等代数教程》）（А.Г.Курош）的定义

如果数环中任何两个数的商仍旧在它的里面（出书不等于0），那么叫这个数环为数域，以后我们叫 $R$ 为有理数域， $D$ 为实数域， $K$ 为复数域，但是 $Z$ 不能叫做整数域，任何数域内都含有有理数数域 $R$

②来自《高等代数》（丘维声）的定义

定义一 设 $K$ 是复数集的一个子集，如果 $K$ 满足：

$(1)0,1 \in K;$

$(2)$ 对于任意的 $a,b \in K$ ，都有 $a \pm b, ab \in K$ ，并且当 $b \neq 0$ 时，有 $\frac{a}{b}\in K$ ，那么称呼 $K$ 是一个数域

数域 $K$ 满足的第 $(2)$ 个条件可以说成： $K$ 对于加、减、乘、除4种运算封闭

6.域

①来自《高等代数》（杨子胥）的定义

$\S 12.5$ 域

本章节来讨论一种特殊的环——域

定义1 设 $R$ 是一个环，如果 $R$ 中有元素 $e$ ，它对 $R$ 中任意元素 $a$ 都有

$ea=ae=a$

则称呼 $e$ 为环 $R$ 的单位元

定义2 设 $R$ 是有单位元 $e$ 的环， $a \in R$ ，如果在 $R$ 中有元素 $b$ 使

$ab=ba=e$

则称 $b$ 为元素 $a$ 的逆元

一个环不一定都有单位元，即使有单位元，也不一定每个元素都有逆元

定义3 设 $F$ 是一个有单位元的交换环，如果 $|F|>1$ 且 $F$ 中每个非零元都有逆元，则称呼 $F$ 是一个域

②来自《高等代数》（丘维声）的定义

定义1 一个有单位元素1 $(\neq 0)$ 的交换环 $F$ ，如果它的每一个非零元素都可逆，即任给 $a \in F$ 且 $a \neq 0$ ，存在 $b \in F$ ，使得 $ab=ba=1$ ，则称呼 $F$ 是一个域

博主注：

还有一种定义方法，是使用除法定义的，其本质实际上就和上两个的是一样的，关于使用除法的定义，可以参见А.Г.Курош的《高等代数教程》

7.象与核

①来自《线性代数》（查建国）的定义

$\S 5.4$ 象与核

在本节中，恒假设 $U$ 与 $V$ 分别是数域 $F$ 上的 $n$ 维和 $m$ 维线性空间

定义1 设 $A:U\rightarrow V$ 是线性映射，集合

$Im(A)=\left \{ A(a)\in V:a \in U \right \}$

称为 $U$ 在 $A$ 下的象，或者 $A$ 的值域，也记为 $A(U)$ ，集合

$Ker(A)=\left \{ a \in U:A(a)=0 \in V \right \}$

成为 $A$ 的核，也记为 $A^{-1}(0)$

8.理想

①来自《近世代数基础》（张禾瑞）的定义

$\S 7$ 理想

现在我们回到一般环的讨论

我们已经知道什么叫做一个子环，在这一节里我们要讨论到一种非常重要的子环，就是理想子环，这种子环在环论里的地位同不变子群里的地位类似

定义环 $R$ 的一个非空子集 $\mathfrak{U}$ 叫做一个理想子环，简称理想，假如

$(i)$ $a,b \in \mathfrak{U} \Rightarrow a-b \in \mathfrak{U}$

$(ii)$ $a \in \mathfrak{U},r \in \mathbb{R}\Rightarrow ra,ar \in \mathfrak{U}$

由于 $(i)$ ，一个理想 $\mathfrak{U}$ 是一个加群，由于 $(ii)$ ， $\mathfrak{U}$ 对于乘法来说是封闭的，所以一个理想一定是一个子环，，但是 $(ii)$ 不仅要求 $\mathfrak{U}$ 的两个元的乘积必须在 $\mathfrak{U}$ 里，而且进一步要求， $\mathfrak{U}$ 的一个任意元同 $\mathbb{R}$ 的一个任意元的乘积都必须在 $\mathfrak{U}$ 里面，所以一个理想所适合的条件比一般子环的要强一点。

我们首先要问，一个环是不是一定有理想？回答是肯定的，因为一个环 $\mathbb{R}$ 至少有以下两个理想：

1.只包含零元的集合，这个理想叫做 $\mathbb{R}$ 的零理想；

2. $\mathbb{R}$ 子集，这个理想叫做 $\mathbb{R}$ 的单位理想

有的环除了这两个理想以外，没有其他的理想，比如说除环。

②来自《交换代数导引》（M.F. Atiyah和I.G. Macedonald）的定义

环 $A$ 中的一个加法子群 $a$ 叫做环 $A$ 的一个理想，如果它具有性质 $Aa\subseteq a$ ，（即若 $x \in A$ 且 $y \in A$ ，则 $xy \in a$ ）， $A$ 中乘法诱导出商群（或同余类环） $A/a$ ， $A/a$ 的元素是 $A$ 对于 $a$ 的陪集，而映射 $\varphi :A \rightarrow A /a$ 将每个元素 $x \in A$ 映到它的陪集 $x+a$ ，是环的满同态

我们经常用到下面这个事实：

命题1.1 在环 $A$ 的包含 $a$ 的那些理想 $b$ 与环 $A/a$ 的理想 $\bar{b}$ 之间存在着保持包含关系的一一对应： $b= \varphi^{-1}(\bar{b})$

设 $f: A \rightarrow B$ 是任一环的同态， $f$ 是核 $f^{-1}(0)$ 是环 $A$ 中的一个理想 $a$ ，而 $f$ 的象 $f(A)$ 是环 $B$ 中的子环 $C$ ，同态 $f$ 导出环同构 $A /a \cong C$

我们有时采用记号 $x\equiv y (mod$ $a)$ ，它等价于 $x-y \in a$

9.费马螺线

①来自百度的定义

费马螺线，是等角螺线的一种，表达式是 $r^2=\theta a^2$

等角螺线，指的是臂的距离以几何级数递增的螺线。设 $L$ 为穿过原点的任意直线，则 $L$ 与等角螺线的相交的角 $A$ 永远相等（故其名），而此值为 $arccot(b)$

等角螺线的表达式可以是 $r=ae^{b \theta}$ 或者 $\theta = \frac{1}{b}ln(\frac{r}{a})$

10.环面

①来自百度的定义

环面（torus）是一个面包圈形状的旋转曲面，由一个圆绕一个和该圆共面的一个轴回转所生成。在拓扑学上，环面是一个定义为两个圆的积的闭合曲面。形似甜甜圈

定义一：与 $S_1 \times S_2$ 同胚的曲面被称为环面，它是亏格为1的可定向闭曲面，通常，环面可以看作由一个长方体按照逆时针方向分别叠合左右两边和上下两边得到的

定义二：若一个线性代数群 $G$ 同构于某个 $D(n,k)$ ，则称 $G$ 是一个环面，联通的可对角化代数群一定是一个环面

参数式：

$x(u,v)=(R+rcosv)cosu,$

$y(u,v)=(R+rcosv)sinu,$

其中 $u,v \in [0,2\pi]$ , $R$ 式管子中心到画面的中心的距离， $r$ 是圆管的半径

直角坐标系中，关于z-轴方位角对称的环面方程是 $[(R-\sqrt{x^2+y^2})]^2+z^2=r^3$

环面是阿贝尔李群

11.莫德尔猜想/莫德尔定理

设 $k$ 为有理数域的有限扩张， $C$ 为 $k$ 上射影光滑(代数)曲线，莫德尔猜想是:若 $C$ 的亏格大于1，则 $C$ 只有有限多个 $k$ 点(即坐标在 $k$ 中的点).

最初形式，这个猜想是说，任一不可约、有理系数的二元多项式，当它的“亏格”大于或等于2时，最多只有有限个解。记这个多项式为 $f(x,y)$ ，猜想便表示：最多存在有限对数偶 $x_i,y_i \in Q$ ，使得 $f(x_i,y_i)=0$

资料来源:

网站：

1.测度的扩张|半代数→代数→σ-代数→完备σ-代数 - 知乎

2.请问半环和半代数（semi-algebra）是一个东西吗？ - 知乎

3.费马螺线_百度百科

4.等角螺线_百度百科

5.环面_百度百科

6.莫德尔定理_百度百科

文献：

1.《半代数及其部分结构的刻画》——[中国，华中师范大学]向长城，魏代俊

2.《代数半代数互推》——百度文库

书籍：

1.《代数几何导引（德文版）》——[瑞士] 马库斯·布罗德曼，哈尔滨工业大学出版社，2018年4月

2.《交换代数导引》——[英国]M.F. Atiyah和I.G. Macedonald，科学出版社，1982年11月

3.《Курс высшей алгебры》——[苏联]А.Г.Курош，Государственяое издательство техника-теоретической литературы，1952

本书是苏联国家技术理论书籍出版社（Государственяое издательство техника-теоретической литературы）于1952年出版的《Курс высшей алгебры》（《高等代数教程》），作者А.Г.Курош（А.Г.库洛什）本书经苏联高等教育部评定成为国立大学和师范学院的教科书，博主使用的是柯召根据1952年第三版翻译，根据1956年第四版修订的中译版《高等代数教程》

4.《高等代数》——[中国]丘维声，高等教育出版社，2015年3月

5.《代数学》——[美国]Thomas W.Hungerford著，[中国]冯克勤译，世界图书出版社，1985年3月

6.《高等代数》——[中国]杨子胥，高等教育出版社，1990年4月

7.《近世代数概论》（下册）——[美国]G·伯克霍夫，S·麦克莱恩[著]，王连祥，徐光善[译]，人民教育出版社，1980年7月

8.《近世代数基础》（1978年修订本）——[中国]张禾瑞，高等教育出版社，1978年3月

9.《线性代数》——[中国]查建国，中国科技大学出版社，1989年4月

nimo毛毛

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
1
评论
代数几何导引（德文版）【瑞士马库斯·布罗德曼（Markus Brodmann）】的读书笔记，翻译和感想（4）

我们之前提到过"半代数几何",先要明白"半代数几何"是什么就要搞清楚什么是"半代数"。在《半代数及其部分结构的刻画》中就有提到关于“半代数”的定义。我将会在这里进行引用这是一篇从百度文库中翻出来的文章，在本文中阐述代数和半代数的关系，代数和半代数的互推，以及代数和半代数互推在计算机中的作用。代数和半代数互推代数和半代数是数学中的两个重要概念，它们在数学中有着广泛的应用。在代数和半代数之间，存在着一种重要的关系，即互推关系。本文将从代数和半代数的定义入手，介绍代数半代数互推的概念和应用。
复制链接

扫一扫