代数几何导引（德文版）【瑞士马库斯·布罗德曼（Markus Brodmann）】的读书笔记，翻译和感想（3）

nimo毛毛

已于 2023-09-01 15:43:04 修改

阅读量6.5k

点赞数 3

分类专栏：代数几何导引（德文版）【瑞士马库斯·布罗德曼】文章标签：学习几何学笔记论文阅读拓扑学抽象代数

于 2023-08-20 08:37:45 首次发布

本文链接：https://blog.csdn.net/nimomath666/article/details/132239032

版权

代数几何导引（德文版）【瑞士马库斯·布罗德曼】专栏收录该内容

4 篇文章

订阅专栏

上一次我们说完了多项式的根图像(Nullstellengebilde von Polynomen)，接着我们说一下关于在复数平面内的圆(Der Kreis im Komplexen)

前文链接：

（1）的原文链接：代数几何导引（德文版）【瑞士马库斯·布罗德曼（Markus Brodmann）】的读书笔记，翻译和感想（1）_nimo毛毛的博客-CSDN博客这是我的第一篇博客，写这篇博客的时候已经是2023年8月5日1点33分了，自然，短是毛病，让各位读者没有读尽兴，应当改正，希望我后面的博客越写越好，做到长短适中，实话讲，作为一个数学兴趣爱好者，并且处于高中阶段，看这本书确实起点过高了，所以也会去做一些低于这本书起点的笔记，如“同胚”这个概念，甚至是一些符号，也是做了相关的笔记，所以可能专业人士和科研人员看起来我的文章过于的细致（甚至可以说是杂碎），过于复杂和细节，愿各位谅解。https://blog.csdn.net/nimomath666/article/details/132114451（2）的原文链接：代数几何导引（德文版）【瑞士马库斯·布罗德曼（Markus Brodmann）】的读书笔记，翻译和感想（2）_nimo毛毛的博客-CSDN博客可能确实拓展的有一点多了，有一些杂碎了，不过我认为多了解一些总归是好的指标集_百度百科超线性收敛_百度百科收敛速度_百度百科《R收敛因子与Q收敛因子的关系》，钱仲范，《同济大学学报》1998年2月第26卷第1期《收敛因子在无穷积分计算中的运用》，梁志清，农海娇，严晓婷，叶玲伶，庞敏，玉林师范学学院学报（自然科学）2018年第39卷第2期%281.1%29f_%7Bi%7D%281.2%29%281.3%29f_%7Bi%7Df_%7Bi%7Dff%28x%29QQ_%7B1%7Dx_%7Bk%7D。https://blog.csdn.net/nimomath666/article/details/132140275

德语原文：

p7部分

中文翻译：

复数平面上的圆。通常，研究代数方程是很简单的，对于所有的解，也就是说是包括研究复数的解，即便人们只对于实数解感兴趣，我们同样乐意去接受这些关于研究代数解的图像的观点（指的是在实数时也研究复数解）。根据一些例子，我们希望可以弄明白，这些方程有哪些必然性(Konsequenzen)。

（1,4）例子：有 $\varepsilon \in \mathbb{R}-\left \{ 0 \right \}$ 。我们观察 $X^{(\varepsilon)}:=V(z_{1}+z_{2}-\varepsilon)$ 这个代数集合在 $\mathbb{C}^{2}$ （复数平面）。以及与之相匹配的实数根的图像 $X^{(\varepsilon)}_{\mathbb{R}}:=X^{(\varepsilon)}\cap \mathbb{R}^{2}$ （代数集合与实数平面的交集），我们很容易理解 $X^{(\varepsilon)}_{\mathbb{R}}$ ，它就是：

博主注：

1. $\mathbb{R}-\left \{ 0 \right \}$ 指的是没有{0}这个的实数集，即非零实数

2. $z_{1},z_{2}$ 可以组成一个二元数组，而这二元数组与所谓的 $\mathbb{R}^{2}$ 的交集，指的便是该二元数组与 $\left \{ (x,y)|x,y \in \mathbb{R} \right \}$ 的交集，即此时该二元数组内元素均为实数

3. := 的意思是“定义，定义为”

4. $X^{(\varepsilon)}$ 的 $\varepsilon$ 表示“样本空间”

5.当 $\varepsilon >0$ 的时候，这个就是在实数平面的解显然就是一个半径 $\sqrt{\varepsilon }$ 的圆，完全可以理解成为 $a^{2}+b^{2}=(\sqrt{\varepsilon })^{2}(a,b \in \mathbb{R})$

我们现在做一个 $X^{(\varepsilon)}$ 的几何图像，我们将复数变量 $z_{j}$ 拆开成为实部和虚部，也就是说我们把它写作：

$z_{j}=x_{j}+iy_{j}$

其中 $x_{1},x_{2,}y_{1},y_{2}$ 为实数变量，我们现在通过 $\mathbb{R}^4$ 来定义 $\mathbb{C}^2$ ，即我们通过点 $(x_{1},x_{2},y_{1},y_{2})\in \mathbb{R}^{4}$ 来定义点 $(z_{1},z_{2})\in \mathbb{C}^2$ ，这样子我们可以将 $X^{(\varepsilon )}$ 理解成为在 $\mathbb{R}^{4}$ 中德集合，由于四维空间（ $\mathbb{R}^{4}$ ）摆脱了我们的直觉，我们想要构造一个从 $X^{(\varepsilon )}$ 到空间 $\mathbb{R}^{3}$ 中的简单曲面 $H^{(\varepsilon )}$ 的同态/同胚

$X^{(\varepsilon )}$ 是所有 $(z_{1},z_{2})\in \mathbb{C}^2$ 的集合，对于所有的 $re(z_{1}+z_{2}-\varepsilon)=im(z_{1}+z_{2}-\varepsilon)=0$ ,re和im分别对应着一个复数里面的实部和虚部，由于 $re(z_{1}^{2}+z_{1}^{2}-\varepsilon )=x_{1}^{2}+x_{2}^{2}-y_{1}^{2}-y_{2}^{2}-\varepsilon$ , $im(z_{1}^{2}+z_{1}^{2}-\varepsilon )=2(x_{1}y_{1}+x_{2}y_{2})$ 是以下方程的解的 $X^{\varepsilon }\subseteq \mathbb{R}^{4}$ （翻译存疑，原文如下： Wegen $re(z_{1}^{2}+z_{1}^{2}-\varepsilon )=x_{1}^{2}+x_{2}^{2}-y_{1}^{2}-y_{2}^{2}-\varepsilon$ , $im(z_{1}^{2}+z_{1}^{2}-\varepsilon )=2(x_{1}y_{1}+x_{2}y_{2})$ ist $X^{\varepsilon }\subseteq \mathbb{R}^{4}$ des Lösungsgebilde des Systems）

博主注：

1.re和im

re和im指的是一个复数里面的实部和虚部，而一个复数等于0，必须它的实部和虚部分别等于0，所以才有了 $re(z_{1}+z_{2}-\varepsilon)=im(z_{1}+z_{2}-\varepsilon)=0$ ，实部和虚部是不能相互抵消的，注意：im(2+3i)=3,re(2+3i)=2（！！！）

2.使用三维

人脑想象不出来四维空间，所以我们使用一个同态/同胚来在三维空间里面描述这个简单曲面 $H^{(\varepsilon )}$ ，而这个简单曲面就是我们后面要提到的“单层旋转双曲面（einschaliges Rotationshyperboloïd）

3.n维欧式几何空间/n维欧几里得空间及其相关：

定义：设n为正整数，由n个实数构成的数组 $x=(x_{1},x_{2},...,x_{n})$ 的全体组成的集合成为n维点或者n维欧几里得空间，记作 $R^{n}$ ，即，

$R^{n}=\left \{ x=(x_{1},x_{2},...,x_{n})|x_{i}\in R,i=1,2,3,...,n \right \}$

相关概念：

为了深入研究行维点集 $R^{n}$ 中领域，有界集，点列收敛等概念，需要对 $R^{n}$ 中的点之间定义距离，为了使问题讨论适用于更广泛的情形，我们对一般的集合给出距离的概念。

①n维欧几里得空间通过距离的定义：

设X是一个非空集合，如果对于X中任何两个元素，x和y都有一个确定的实数，记为 $\rho (x,y)$ ,与之对应，且满足下面三条件，则称 $\rho$ 为X上的距离，称 $\rho (x,y)$ 为x,y之间的距离，而称X是以 $\rho$ 为距离的距离空间(或度量空间)，记为 $(X,\rho )$ ，那么三个条件为：

（A）非负性， $\rho (x,y)\geqslant 0$ ，而且 $\rho (x,y)=0$ 当且仅当x=y；

（B）对称性， $\rho (x,y)=\rho (y,x)$ ；

（C）三角不等式 $\rho (x,y)\leqslant \rho (x,z)+\rho (z,y)$ ，这里z也是X中的任意一个元素。

对于 $R^{n}$ 中任意两个点 $x=(x_{1},x_{2},...,x_{n})$ , $y=(y_{1},y_{2},...,y_{n})$ 定义实函数 $\rho (x,y)=\left [ \sum_{i=1}^{n}(x_{i}-y_{i})^{2} \right ]^{\frac{1}{2}}$ 则 $\rho (x,y)$ 满足距离三条件(A)(B)(C)，称 $\rho$ 为 $R^{n}$ 上的欧几里得距离，称 $(R_{n},\rho )$ 为欧几里得空间。

②邻域定义：

设 $P_{0}\in R^{n}$ 是一个固定点， $\delta$ >0为一个实数，则集合 $\left \{ P|\rho (P,P_{0})<\delta \right \}$ 称为以 $P_{0}$ 为中心的 $\delta$ 邻域，记作 $U(P_{0},\delta )$

$P_{0}$ 称为邻域中心，而 $\delta$ 为邻域半径，显然在 $R,R^{2},R^{3}$ 中的邻域 $U(P_{0},\delta )$ 就分别是以 $P_{0}$ 为中心以 $\delta$ 为半径的开区间，开圆和开球。

容易证明有以下性质：

（A）对于 $Q\in U(P)$ ，存在 $U(Q)\subset U(P)$

（B）对于 $P\neq Q$ 则存在 $U(Q)$ 和 $U(P)$ 使得 $U(Q)\cup U(P)\neq \varnothing$

③收敛点列的定义

设 $P_{k}$ 是 $R^{n}$ 中的一个点列， $P_{0}\in R^{n}$ ，如果 $k\rightarrow \infty$ 时，有 $\rho (P_{k},P_{0})\rightarrow 0$ ，则称呼点列 $\left \{ P_{k} \right \}$ 收敛于 $P_{0}$ ，记为 $\lim_{k\rightarrow \infty }P_{k}=P_{0}$ 或者 $P_{k}\rightarrow P_{0}(k\rightarrow \infty )$

用邻域语言来说就是：

$\lim_{k\rightarrow \infty }P_{k}=P_{0}$

对于 $P_{0}$ 的任何邻域 $U(P_{0})$ ,存在 $K\in N^{+}$ ，使当 $k\rightarrow K$ 时， $P_{k}\in U(P_{0})$

用“ $\varepsilon -N$ ”语言来说：

$\lim_{k\rightarrow \infty }P_{k}=P_{0}$

对于任意的 $\varepsilon >0$ ，存在 $K \in N^{+}$ ，使当k>K时, $\rho (P_{k},P_{0})<\varepsilon$ 。

④距离定义

设两个非空子集，A,B的距离定义为

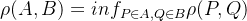
$\rho (A,B)=inf_{P \in A,Q \in B}\rho (P,Q)$

4.计算

说明 $re(z_{1}^{2}+z_{1}^{2}-\varepsilon )=x_{1}^{2}+x_{2}^{2}-y_{1}^{2}-y_{2}^{2}-\varepsilon$ 和 $im(z_{1}^{2}+z_{1}^{2}-\varepsilon )=2(x_{1}y_{1}+x_{2}y_{2})$ ,不妨设 $z_{1}=x_{1}+iy_{1},z_{2}=x_{2}+iy_{2}$

则有

$z_{1}^{2}+z_{2}^{2}-\varepsilon$

$=(x_{1}+iy_{1})^2+(x_{2}+iy_{2})^2-\varepsilon$

$=x_{1}^2-y_{1}^2+x_{2}^{2}-y_{2}^{2}-\varepsilon+2ix_{1}y_{1}+2ix_{2}y_{2}$ $=x_{1}^{2}+x_{2}^{2}-y_{1}^{2}-y_{2}^{2}-\varepsilon +2ix_{1}y_{1}+2ix_{2}y_{2}$

显然可得，

$re(z_{1}^{2}+z_{1}^{2}-\varepsilon )=x_{1}^{2}+x_{2}^{2}-y_{1}^{2}-y_{2}^{2}-\varepsilon$

$im(z_{1}^{2}+z_{1}^{2}-\varepsilon )=2(x_{1}y_{1}+x_{2}y_{2})$

显然，爱查资料的人人已经发现，在数学中有一些词语都是以“同”字开头的，也都与映射等有关，不放我们在此做一个辨析吧，“同”子开头的大致有这么几个次“同态、同构、同胚、同伦、同痕、同调”

5.同胚:

拓扑学概念，同胚是两个拓扑空间之间的双连续映射，同胚就是拓扑空间中的同构。在拓扑学中，同胚是两个拓扑空间的双连续函数，同胚即拓扑空间的同构，即它们是保持给定空间的所有拓扑性质的映射，如果两个空间存在同胚，那么在拓扑理论中，称为“同胚的”（即间在连续改变形状后还能保持不变的一些性质，也就是说，我们将一个图形通过弯曲，拉大，缩小等操作之后，能够变成另一个图形），在拓扑角度上来看，这两个空间是相同的。

性质：2个拓扑空间 $\left \{ X,T_{X} \right \}$ 和 $\left \{ Y,T_{Y} \right \}$ 之间的函数 $f:X\rightarrow Y$ 称之为同胚，如果它具有以下性质：

·f是双射

·f是连续的

·反函数f也是连续的

满足以上2个性质的函数有时成为双连续函数

6.同构：

在抽象代数中，同构为保持代数结构（如群，适量空间）的双射，在更加一般的范畴论语言中，同构指的是一个态射，且存在另一个态射，使得两者的复合是一个恒等态射。一个 $A$ 与 $\bar{A}$ 之间的 —— 映射 $\oslash$ $\O$ 对于代数运算的o和 $\bar{o}$ 来说的A与 $\bar{A}$ 之间的同构映射，简称同构，假如在 $\oslash$ 之下，不管a,b是A的那两个元素，只要 $a\rightarrow \bar{a},b\rightarrow \bar{b}$ ，就有 $a^{\circ}b=\bar{a}^{\circ}\bar{b}$

来自知乎的Nick Yin在其视频中我找到以下定义：

let $<S,*>$ and $<S^{'},*^{'}>$ be binary algebraic structures.An Isomophorism of S with S' is a one-to-one function $\phi$ mapping.S onto S' s.t. $\phi$ is homomorphism

7.同态

代数学的名词，尤其是和范畴论和模型论有关系，是范畴论的基础概念，一般指的是群的同态或者是环的同态。

群的同态：设(M,*)和(S,·)是两个群，σ:M→S，∀a,b∈M，有σ(a*b)=σ(a)·σ(b)，则称σ为M到S的同态或群映射。实际上同态是一种很特殊的映射方式，来自知乎的Nick Yin在其视频中我找到以下定义：

let $<S,*>$ and $<S^{'},*^{'}>$ be binary algebraic structures. A homomorphism $\phi :s\rightarrow s^{'}$ satisfies

$\phi (x*y)=\phi (x)*'\phi(y),x,y \in S$

我个人认为其实这两种定义是一样的。

8.同伦

拓扑学名词，指的是在拓扑空间角度描述两个对象之间的“连续变化”。两个如果可以通过一系列连续的变化（如拉大，缩小，旋转）从一个变到另一个，那么就称这两个拓扑空间同伦。下面是一个我在网上找到的一些其他的定义和解释：

同伦是指两个或多个函数在时间上的连续变化。在数学上，同伦通常被表示为两个函数之间的一个等价关系，这个等价关系定义了一组允许的变换。这些变换通常被称为同伦变换。同伦变换是指在函数定义域内进行的一类连续变换，这些变换可以将一个函数逐渐变为另一个函数。具体来说，设和是的两个函数，如果存在一个函数，使得当趋近于时，趋近于，则和是同伦的。

①函数的同伦

$f,g:X\rightarrow Y$ 给定的两个拓扑空间X和Y，考虑两个连续函数，若存在一个连续映射 $H:X\times [0,1]\rightarrow Y$ 使得

$\forall x \in X, H(x,0)=f(x)$

$\forall x\in X,H(x,1)=g(x)$

则称f,g在Y中同伦

9.同痕

同痕实际上是同伦的加强版，我们进一步要求所论的函数 $f:X\rightarrow Y$ 和 $g:X\rightarrow Y$ 是嵌入，并且要求两者间可用一族嵌入映射相连。

定义：f和g被称为是同痕的，当且仅当 $H:X\times [0,1]\rightarrow Y$ 使得

$\forall x \in X, H(x,0)=f(x)$

$\forall x \in X, H(x,0)=f(x)$

对所有 $t \in [0,1]$ ，映射 $h_{t}(x)=H(x,t)$ 是一个嵌入映射。

同痕的概念在纽结理论中格外重要，若两个结同痕，则我们视之相等，换言之，可以再不使结拉扯段或相交的条件下批次连续的变形。

10.同调

很抱歉，我并没有在百度词条中找到任何关于同调的概念，不过我在知乎中找到了一个很好的定义，在“代数拓扑中的同调和上同调有哪些联系”中Yan Z答主给出了一下的来自维基百科的定义:

首先定义一个分次的(graded)链复形(chain complex) $C_{*}=\left \{ C_{n}|n\in\mathbb{Z} \right \}$ ，一般来说链复形是一连串的abelian group,而在这个链复形上有一个降次运算 $d_{n}:C_{n}\rightarrow C_{n-1}$ ，一般叫做边界运算(boundary map)这个运算满足一个条件，即做两次之后是0： $d_{n-1}^{\circ}d_{n}:C_{n}\rightarrow C_{n-2}=0$

我们称一个闭链(closed chain or cycle) $x\in C_{n+1}$ 使得 $d_{n+1}(z)=y$

显而易见的，边缘一定是闭链，而闭链不一定是边缘，我们把n维同调定义成链商其边缘（作为交换群的商群）

在资料来源中，有一篇推荐的“同调”的文章，非常的好，有兴趣的人可以看看。

我们首先处理 $\varepsilon >0$ 的情况，我们定义 $V^{+}$ 为所有点 $(x_{1},x_{2},y_{1},y_{2})\in \mathbb{R}^{4}$ 的集合，这些的等式(i)(b)符合并且 $(x_{1},x_{2})\neq 0$ ，由于很明显 $\varepsilon >0$ ， $X^{(\varepsilon )}\subseteq V^{+}$ 。我们使用坐标u,v,w来描述空间 $\mathbb{R}^{3}$ 。定义 $W\subseteq \mathbb{R}^{3}$ 为集合 $\left \{ (u,v,w)|(u,v)\neq (0,0) \right \}$ ，这个集合是来自于 $\mathbb{R}^{3}$ 空间通过除去w轴来的产生的，现在定义一个映射 $\varphi ^{+}:V^{+}\rightarrow W,\psi ^{+}:W\rightarrow V^{+}$ ，通过以下法则

博主注：

1.关于映射

这个实际上是两个互逆的映射，简单的将 $(u,v,\frac{-vw}{\sqrt{u^{2}+v^{2}}},\frac{uw}{\sqrt{u^{2}+v^{2}}})$ 代入 $(x_{1}.x_{2},y_{1},y_{2})$ 可以重新得到(u,v,w)。这两个互逆的映射，一个是将四元数组映射成为三元数组，一个则是将三元数组映射为四元数组

显然这两个映射是不变的，我们现在立即计算，这两个相互逆的 $\varphi ^{+},\psi ^{+}$ ，那么我们得到一个同态/同态

我们在 $\mathbb{R}^{3}$ 中观察曲面

（我们此时同样考虑了 $\varepsilon <0$ 的情况）。 $H^{(\varepsilon )}$ 的形成可以理解成为在(u,w)平面上的双曲线 $u^{2}+v^{2}-\varepsilon =0$ 沿着w轴进行自转(rotieren)， $H^{(\varepsilon )}$ 就是einschaliges Rotationshyperboloïd（单层旋转双曲面），根据方程(i)(a),(b)我们可以立即得出， $\varphi ^{+}(X^{(\varepsilon) })\subseteq H^{(\varepsilon )},\psi ^{+}(H^{(\varepsilon) })\subseteq X^{(\varepsilon )}$ ，也就是说 $\varphi ^{+}(X^{(\varepsilon) })=H^{(\varepsilon )}$ ，因此，我们可以将我们正在寻找的同胚 $\varphi ^{(\varepsilon) }$ 定义为约束映射/限制图像（？？？德语：Einschränkungsabbildung） $\varphi^{+} | X^{(\varepsilon )}$ 并得到以下情况

$\varphi^{+}$ 同样描绘了开集 $W\subseteq \mathbb{R}^{3}$ 的 $V^{+}$ 同胚并且使 $X^{(\varepsilon )}$ 转化成为双曲面 $H^{(\varepsilon )}$ 。 $H^{(\varepsilon )}$ 是 $X^{(\varepsilon )}$ 的一个在拓扑上不动的图像

博主注：

1.einschaliges Rotationshyperboloïd（单层旋转双曲面）

不要被这个名字虎到了，其实所谓的“单层旋转双曲面”就是一个双曲线沿着其中轴进行旋转，所得到的的立体图形就是所谓的“单层旋转双曲面”，如图

来自b站，博主尼莫毛毛，即我自己

我们现在来看一下这个， $\varphi (X^{(\varepsilon)}_{\mathbb{R}})$ 是 $H^{(\varepsilon )}$ 的“腰圆”(Taillenkreis): $\varphi (X^{(\varepsilon)}_{\mathbb{R}})=T^{(\varepsilon )}:=\left \{ (u,v,w)\in H^{(\varepsilon) }|w=0 \right \}$

当 $\varepsilon <0$ 时候，我们定义 $V^{-}$ 作为所有点 $(x_{1},x_{2},y_{1},y_{2})\in\mathbb{R}^{4}$ ，其中满足等式(i)(b)的也要满足 $(y_{1},y_{2})\neq(0,0)$ ，然后即有 $X^{(\varepsilon )}\subseteq V^{-}$ 。我们现在通过以下法则定义两个互逆的映射 $\varphi ^{-}:V^{-}\rightarrow W,\psi ^{-}:W\rightarrow V^{-}$ ：

并且我们现在再次获得了一个同胚

这有 $\varphi ^{-}(X^{(\varepsilon)}_{\mathbb{R}})=H^{(\varepsilon) }$ ，那么我们可以设置一个 $\varphi ^{(\varepsilon )}:=\varphi ^{-}|X^{(\varepsilon )}$ ，并且得到以下情况

我们将 $X^{\varepsilon }_{i\mathbb{R}}$ 记为 $X^{(\varepsilon )}$ 的纯虚数点 $\left \{ (z_{1},z_{2})\in X^{(\varepsilon)} | x_{1}=x_{2}=0 \right \}$ ，那么我们会立即清楚 $\varphi ^{(\varepsilon )}(X^{(\varepsilon )}_{i\mathbb{R}})=T^{(\varepsilon )}$

我们现在选择 $\varepsilon >0$ ，然后显然可以得到 $H^{\varepsilon }=H^{-\varepsilon }$

$X^{(\varepsilon) }$ 和 $X^{(\varepsilon )}$ 是同胚的，尽管 $X^{(\varepsilon )}_{\mathbb{R}}\approx T^{(\varepsilon )}$ 和 $X^{(-\varepsilon) }_{\mathbb{R}}=\varnothing$ 不是。我们同样也可以理解，我们观察一个显然的同胚，即通过 $(z_{1},z_{2})\mapsto (iz_{1},iz_{2})$ 来定义的映射 $\tau :\mathbb{C}^{2}\rightarrow \mathbb{C}^{2}$ ，我们通过 $\mathbb{R}^{4}$ 来定义 $\mathbb{C}^{2}$ ，那么 $\tau$ 是可以描述一下的规则

并且这关系到 $\tau (V^{+})=V^{-}$ ，特别是它关系到这个交换圈

下图在 $\mathbb{R}^{3}$ 中生动形象的展示了 $\varepsilon >0$ 的情况

说明：这个映射 $\varphi ^{(\varepsilon )}:X^{(\varepsilon )}\rightarrow H^{(\varepsilon )}$ 提供了不仅仅是 $X^{(\varepsilon )}$ 的一个在拓扑角度非常真实的图像。并且 $V^{+},V^{-}$ 都是在 $\mathbb{R}^{4}$ 的微分子流形，而W是在 $\mathbb{R}^{3}$ 中的，而 $\varphi ^{+}:V^{-}\rightarrow W,\varphi ^{-}:W \rightarrow V^{-}$ 是微分同胚，特别是 $H^{(\varepsilon )}$ 是一个 $X^{(\varepsilon )}$ 微分同胚的图形。因为 $H^{(\varepsilon )}$ 是一个W的一个微分子流形，所以 $X^{(\varepsilon )}$ 是一个 $V^{+} or V^{-}$ 的这样的微分流形。同样 $X^{(\varepsilon )}$ 是 $\mathbb{R}^{4}$ 的微分子流形。

博主注：

1.腰圆

在einschaliges Rotationshyperboloïd（单层旋转双曲面）中最细的那个圆，也就是本条注释之前最后一张图中标黑的一个圆，这个就是“腰圆”

2.和《微分流形初步》【陈维恒】一样的思路

博主经过自己考证和研究，个人认为要明白什么是微分流形和微分就要先弄明白什么是流形，在弄明白什么是拓扑流形和微分流形之后，在搞明白什么是微分子流形/子流形（虽然这个是废话，但至少个人认为还是有必要说一下）实际上拓扑流形和微分流形由流形来定义，子流行由微分流形定义，所以才有了这样的顺序，博主自己的笔记实际上并没有抄完，因为这边的内容特别多，但是我可以在这里全部都整理给大家。

其实思路和《微分流形初步》【陈维恒】中的一样，但是在这里，可能会给出很多定义，所以我们需要很多预备知识。

3.预备知识

1)豪斯道夫空间(Hausdorff space)

在《流形的拓扑学》（苏况存）的一书中有提到“以后但凡提到拓扑空间总是设它为Hausdorff空间”那么什么是“豪斯道夫空间”呢？

豪斯道夫空间又称为 $T_{2}$ 空间，在拓扑学和相关的数学分支中，豪斯多夫空间、分离空间或 $T_{2}$ 空间是其中的点都“由邻域分离”的拓扑空间，简单来说就是具有“可分离性”的拓扑空间。在众多可施加在拓扑空间上的分离公理中，“豪斯多夫条件”是最常使用和讨论的。它蕴涵了序列、网和滤子的极限的唯一性。豪斯多夫得名于拓扑学的创立者之一费利克斯·豪斯多夫。豪斯多夫最初的拓扑空间定义把豪斯多夫条件包括为公理。我们不得不承认，豪斯道夫空间在数学分析中的广泛应用，可以说，实数就是豪斯道夫空间，必须要承认的是，所有的度量空间都是豪斯道夫空间，即一般拓扑空间就是豪斯道夫空间，豪斯道夫空间就是拓扑空间，但是拓扑空间不一定是豪斯道夫空间。

①定义：

A topological space is called Hausdorff if for each $x_{1},x_{2}$ distinct points in X, there exists open set $U_{1},U_{2}$ , so that $x_{1}\in U_{1},x_{2}\in U_{2} , U_{1}\cap U_{2}=\varnothing$ .

换成中文就是：

豪斯道夫空间中的两点 $x_{1},x_{2}$ 都属于X，他们是被“邻域”所隔开的， $U_{1},U_{2}$ 分别是 $x_{1},x_{2}$ 的邻域， $U_{1}\cap U_{2}=\varnothing$ 意思就是他们的邻域没有任何交集，其交集是空集

豪斯道夫空间的定义实际上是通过其性质来定义的空间。

其中如果任何两个拓扑可区分的点可以由邻域分离，X是预正则的，有时候也称呼X为 $R_{1}$ 空间（预正则空间是 $R_{1}$ 空间）

②豪斯道夫空间的例子和反例:

例子：最简单的是T1空间而非T2空间的拓扑的例子是余有限空间。

反例：伪度量空间典型的不是豪斯多夫空间，但是它们是预正则的。

③豪斯道夫空间的局部紧性

设X为豪斯多夫空间，则以下条件等价：

（1）X为局部紧空间；

（2）X的每点有预紧邻域；

（3）X的预紧开集组成的基。

④豪斯道夫空间的基本性质

（1）所有的正则空间都是预正则空间，也都是豪斯道夫空间

（2）豪斯道夫空间具有可继承性和可乘性，即豪斯道夫的子空间和积空间都是豪斯道夫空间，并且积空间是闭集的。

（3）一个拓扑空间，不是豪斯多夫空间，但是可以序列极限唯一

（4）豪斯道夫空间中的极限是唯一的

关于豪斯道夫空间和其他空间的联系：拓扑空间是豪斯多夫空间，当且仅当它是预正则空间和柯尔莫果洛夫空间的二者(就是说独特的点是拓扑可区分的)。拓扑空间是预正则空间，当且仅当它的柯尔莫果洛夫商空间是豪斯多夫空间。

2)柯尔莫果洛夫空间(Колмого́ров Пространство)

安德烈·柯尔莫果洛夫（Андре́й Никола́евич Колмого́ров），苏联数学家，现代概率论之父，柯尔莫果洛夫空间即 $T_{0}$ 空间。对于一个拓扑空间X，如果对于X的每一对不同的点，其中至少有一个具有不包含另一个的邻域，那么该拓扑空间就是 $T_{0}$ 空间。在 $T_{0}$ 空间中，所有点在拓扑上都是可区分的。

大可以理解柯尔莫果洛夫空间是豪斯道夫空间的一种条件弱化形式，限制更少，但绝对不是弱豪斯道夫空间！

3)弱豪斯道夫空间(feeble Hausdorff space)

弱豪斯道夫空间实际上是和紧豪斯道夫空间息息相关的。若对任何从紧豪斯多夫空间K到X的映射 $g:K\rightarrow X$ ， $g(K)$ 为X的闭子集，则X是弱豪斯多夫空间。若X是弱豪斯多夫空间，则 $g(K)$ 为X的紧豪斯多夫子空间。

4)紧空间(compact space)

拓扑学名词，指的是拓扑空间X的任何开覆盖都有有限子覆盖，X就是紧空间，紧豪斯道夫空间是正规空间

5)正规空间(normal space)

一个一般拓扑学名词，设X为拓扑空间，对X的任何不相交闭集 $F_{1},F_{2}$ ，存在X的不相交开几何 $G_{1},G_{2}$ ，使得 $F_{1}\subset G_{1},F_{2}\subset G_{2}$ ，则称X为正规空间

6)拓扑空间(topological space)

拓扑空间是最重要，最中心地位的，最具有同一性质的概念。

①拓扑空间的定义

给定集合 $X$ 和它的一个子集族 $\boldsymbol{O}\subseteq P(x)$ ，如果 $\boldsymbol{O}$ 满足以下条件 $\boldsymbol{O1-O3}$ ，则把 $\boldsymbol{O}$ 称为 $X$ 的拓扑， $\boldsymbol{O}$ 中的每一个集合都是 $X$ 的开集，并且 $(\boldsymbol{O},X)$ 称为拓扑空间。

$\boldsymbol{O1}:\varnothing \in \boldsymbol{O},X\in \boldsymbol{O};$

$\boldsymbol{O2}:if U_{1},U_{2}\in \boldsymbol{O},so U_{1}\cap U_{2}\in\boldsymbol{O};$

$\boldsymbol{O3}:$ 设 $\Lambda$ 为指标集，如果集族 $\left \{ U_{\lambda }|\lambda \in\Lambda \right \}\in\boldsymbol{O}$ ，那么 $\bigcup _{\lambda \in\Lambda }U_{\lambda }\in\boldsymbol{O}$ ；

7)坐标卡

①来自百度+知乎定义

坐标卡是流形上的局部坐标系。设 $X$ 是拓扑空间，称 $\phi =\left \{ U_{i},\varphi _{i}|i \in \Lambda \right \}$ 是它的图册，如果 $u=\left \{ U_{i} \right \}i\in\Lambda$ 是 $X$ 的开覆盖，且对于任何 $i\in\Lambda$ ，是从 $U_{i}$ 到 $\mathbb{R}^{n}$ 的局部同胚。 $(U_{i},\varphi _{i})$ 称为坐标卡，流形是非欧空间和欧几里得空间的一种联系，而这种联系实际上就是坐标卡，坐标卡本身和局部坐标系没有什么区别，但局部坐标系更加严谨和严格限制一些，而局部坐标系就是坐标系以物体的中心为坐标原点，物体的旋转、平移等操作都是围绕局部坐标系进行的，这时，当物体模型进行旋转或平移等操作时，局部坐标系也执行相应的旋转或平移操作。

②来自陈维恒《微分几何初步》的定义+例子

这里我们小小的引入一下n维流形的概念，以更加清楚地阐述坐标卡（局部坐标系）这个概念，在之后我们会有更加深刻和详细的对于n维流形的阐述。



        假定 $R^{n}$ 是欧式几何空间，点 $p\in R^{n}$ 的第i个坐标记为 $(p)^{i}$ ，即 $()^{i}$ （是的，你没看错，就是()^i）是 $R^{n}$ 中的第i个坐标函数

        定义1.1        设M是一个Hausdorff空间，若M的没一点p都有一个开邻域 $U\subset M$ ，使得U和n维欧式几何空间 $R^{n}$ 中的一个开子集是同胚的，则称M是一个n维拓扑流形，简称n维流形

        假定在定义1.1中所提到的同胚是 $\varphi :U\rightarrow \varphi (U)\subset R^{n}$ ，其中 $\varphi (U)$ 是 $R^{n}$ 中的开集，则称呼 $(U,\varphi )$ 为流形M的一个坐标卡，并且把象点 $\varphi (p)$ 是在 $R^{n}$ 中的坐标 $(\varphi (p))^{i}$ 成为点 $p\in U$ 的坐标，记为 $x^{i}(p)=(\varphi(p))^{i}$ （严格的说，坐标 $x^{i}$ 依赖于同胚 $\varphi$ ，因此应该记录为 $x^{i}_{\varphi }$ ,为了简单记号期间，我们把 $x^{i}$ 看做对定于同胚 $\varphi$ ，即 $x^{i}(p)=(\varphi(p))^{i}$ ；对应于同胚 $\psi$ 的坐标系则用另外一个字母表示，例如 $y^{i}(p)=(\psi(p))^{i}$ ，我们也称呼 $(U;x^{i})$ 为流形M的一个局部坐标系，显然，拓扑流形必定是局部紧致的，即每一点 $p\in M$ ，必有p的一个邻域V，使得 $\bar{V}$ 是紧致的【笑死了，我半天都没找到另一半括号在哪里】

8）张量

好了，是时候回归正题了，我想通过上面的知识预备已经足够我们去理解流形，微分流形，和子流形了

4.流形，微分流形和子流形

一：流形（拓扑流形）

①来自百度和知乎的定义和相关概念：

具有局部欧几里得空间性质的空间，在数学用于描述几何物体，在物理上，经典力学的相空间和构造广义相对论的时空模型的四维伪黎曼流形都是流形的实例,

1）n维流行的概念

在J.L.Largrange的力学中已经出现，在19世纪中期人已经知道了n维欧几里得空间（百度上写的Euclid空间）是n个实变量的连续统，但是一般n流形的概念是B.Riemann为了研究微分几何而引进的，正如曲线运动成为曲面一样，n维流形就是把无限多个(n-1)维的流形按照一维流形的方式放在一起而形成的）（PS：圆周是一种一维流形，球体的表面就是二位的流形）

2）定义

在n维欧几里得空间 $\mathbb{R}^{n}$ ,由 $x_{1}\geqslant 0$ 定义的半空间用 $H^{n}$ 表示。豪斯多夫空间M，当每点p具有与 $\mathbb{R}^{n}$ 或 $H^{n}$ 同胚的开邻或U(p)时，称为n维拓扑流形， $U(p)\approx H^{n}$ （同胚）的点p的全体 $\partial M$ 被称为M的面源，其补集 $M_{0}=M-\partial M$ 称为M的内部， $\partial M=\varnothing$ 的流形被称为无边缘流形。

n维流行M的边缘 $\partial M$ 是n-1维无边缘流形，紧的无边缘的流通流行称为开流形，存在连通的但非仿紧的拓扑流形，一味地这种流行被称为长直形

3）流形反例

流形不必是相连通的（整个只有一片）所以两个不相交的圆周也是拓扑流形，流形不必是封闭的，所以不带两个端点的线段也是流形，流形不必有限，所以抛物线也是一个拓扑流形。但是我们拍出来像两个相切的圆（他们共享一个点并且形成8字形）的例子，切点附近的任意小的部分都不同胚与欧式空间的任何一个开集。

4）重要流形

拓扑流形：拓扑流形为最为容易定义的流形，它局部看起来像一些“普通的”欧式空间 $R_{n}$ 。形式化的来说，一个拓扑流形是一个局部同胚于一个欧式空间，这表示每个店都有一个邻域，它有一个同胚（连续映射，并且其逆也是连续的），将它映射到 $R^{n}_{+}$ 。这些同胚是流行的坐标图。

微分流形：微分流形是微分几何与微分拓扑的主要研究对象，是三维欧式中曲线和曲面概念的推广，可以有更高的维数，而不必有距离和度量的概念。

②来自梅加强《流形和微分几何初步》的定义及其相关概念

        流形是一种特殊的拓扑空间, 是欧氏空间中曲线, 曲面的推广. 在微积分中, 我们曾研究过曲线的弧长, 曲面的面积等问题. 在古典微分几何中, 我们进一步研究了曲线和曲面的 “弯曲” 性质, 发展出了重要的曲率概念. Gauss 发现, 曲面的曲率实际上只依赖于曲面的第一基本形式, 这为将曲面从欧氏空间中抽象出来进行研究提供了很好的动机. 此外, Gauss-Bonnet 定理将几何量 (曲率) 和拓扑量联系在一起, 从而为用几何手段研究拓扑问题提供了启发. 现代微分几何和拓扑学的主要研究对象就是流形。

所谓拓扑空间指的是一个配对 $(X,\tau )$ ，其中X为一个集合， $\tau$ 也是一个集合，其元素都是X的中的子集，并且满足以下条件：

（1） $\varnothing ,X\in \tau;$

（2） $\tau$ 中有限个元素之交仍属于 $\tau$ ;

（3） $\tau$ 中的任意多个元素之并仍属于 $\tau$

这样的 $\tau$ 称为X上的一个拓扑， $\tau$ 中的元素称为开集，拓扑空间是点击拓扑学或者一般拓扑学的研究对象，人们研究连续性质以及在连续变换下不变的性质，为了研究微分性质，必须对拓扑空间加进一步的的限制，在点集拓扑中，具体可数拓扑基的拓扑空间称为 $A_{2}$ 的，具有Hausdorff（豪斯道夫）性质的拓扑空间被称为 $T_{2}$ 的。

        定义1.1.1( $C^{r}$ 的流形)设M是具有 $A_{2},T_{2}$ 性质的拓扑空间，如果存在M的开覆盖 $\left \{ U_{a} \right \}_{a\in \mathbb{R}^{n}}$ 以及相应的连续映射族 $\varphi _{a}:U_{a}\rightarrow \mathbb{R}^{n}$ ，使得

        （1） $\varphi _{a}:U_{a}\rightarrow \varphi _{a}(U_{a})\subset \mathbb{R}^{n}$ 为从欧式空间开集 $\varphi _{a}(U_{a})$ 上的同胚；

        （2）当 $U_{\alpha }\cap U_{\beta }\neq \varnothing$ ,如下的转换映射

$\varphi _{\beta } { }^{\circ}\varphi _{\beta }^{-1}:\varphi _{a}(U_{a}\cap U_{\beta })\rightarrow \varphi _{\beta }(U_{a}\cap U_{\beta })$

为 $C^{r}(r\geqslant 1)$ 映射，则称M为 $C^{r}$ 流形

        我们称呼 $\left \{ U_{\alpha } \right \}$ 或 $\left \{ (U_{a},\varphi _{a}) \right \}$ 为M的局部坐标映射， $(U_{a},\varphi _{a})$ 我一个局部坐标系， $U_{a}$ 为局部坐标邻域， $\varphi _{a}$ 为局部坐标映射，设 $p \in U_{a}$ ，记 $x^{i}(p)$ 为 $\varphi_{a} (p)$ 的第i个欧式坐标， $x^{i}:U_{a}\rightarrow \mathbb{R}$ 为第i个坐标函数，有时也称呼 $\left \{ x^{i} \right \}=\left \{ x^{1},x^{2},...,x^{n} \right \}$ 为p附近的局部坐标，定义中的n称为流形M的维数，记为n=dim M,为了强调流形的维数，有时也把M记为 $M^{n}$ 。

我们就流形的概念作一些解释:

• 如果所有的转换映射都只是 $C^{0}$ (连续) 的, 则称 M 为拓扑流形. 当 $1\leqslant r<\infty$ 时, 称 M 为 $C^{r}$ 微分流形. 如果转换映射都是无限次可微的, 则称 M 为 $C^{\infty }$ 流形或光滑流形. 当转换映射都是实解析 (记为 $C^{\omega }$ ) 时, 称 M 为实解析流形。

• 设 U 为 M 上的开集, $\varphi :U\rightarrow R^{n}$ 为连续映射, 且 $\varphi$ 的像为开集, $\varphi$ 到其像上是同胚. 如果 $\varphi$ 和 $\varphi _{a}$ 之间的转换映射均为 $C^{r}$ 的, 则称 $(U,\varphi )$ 和局部坐标覆盖 $\left \{ U_{a},\varphi _{a} \right \}$ 是 $C^{r}$ 相容的. 利用选择公理容易证明, 对于任何一个局部坐标覆盖 $\left \{ (U_a,\varphi _a) \right \}$ , 均存在一个包含它的 “最大” 的局部坐标覆盖 $\mathfrak{D}$ , 使得任何与 $\mathfrak{D}$ 均 $C^{r}$ 相容的局部坐标系 $(U,\varphi )$ 都含于 $\mathfrak{D}$ 之中. 我们把这样的 $\mathfrak{D}$ 称为拓扑流形 M 的一个 $C^{r}$ 微分构造或微分结构.

• 存在这样的拓扑流形的例子, 该拓扑流形上不存在任何相容的微分构造; 另一方面, 可以证明 (这是微分拓扑学的内容), 给定一个 $C^{r}(r\geqslant 1)$ 微分构造, 一定存在一个相容的 $C^{\infty }$ 微分构造. 为了方便起见, 在没有明确说明的情况下, 下面的微分流形是指光滑流形。

④来自梅向明《微分流形和黎曼几何》的定义和相关概念

     2.拓扑流形的定义

        在局部微分几何中，曲面的参数表示就是通过同胚 $\varphi$ 将 $R^{2}$ 的一个开域与曲面片等同起来，这样就在曲面上引进了曲纹坐标，但是用一块平面来表示一块去面的半满只是局部才能办得到，当考虑整体问题是，例如考虑整个球面，由于它和平面的拓扑性质不同，平面到球面的整体和微分同胚是不存在的，换言之，无法在整个球面上引进一种单一的坐标使它的 $R^{n}$ 或者 $R^{n}$ 的开集一一对应

当然，可以把球面看成两个半球面粘合起来的，而在每个半球面上可以引进坐标，关键是要求在连结的地方能粘合得光滑，以便使用微积分的工具，像这种有几块同胚于欧式空间的开域的片粘合起来便得到的拓扑空间就是“流形”，下面给出严格的定义

        定义1        一个拓扑空间M，满足

        （1）M是Hausdorff的；

        （2）M是局部欧式的，即对于 $\forall P \in M$ ，存在P的邻域U，使得

$\varphi :U\rightarrow R^{n}$

是U到 $\varphi (U)\leqslant R^{n}$ 的同胚，且 $\varphi (U)$ 是 $R^{n}$ 的开集

        （3）M有可数的拓扑基

则M称为n维拓扑流形，记为n-流形

二：微分流形：

①来自百度和知乎定义和相关概念

微分流形一般也称之为光滑流形，是拓扑学和几何学中一类重要的空间，是带有微分结构的拓扑流形

1)定义

一个 $C^{k}$ 类n维微分流形是具有 $C^{k}$ 类微分结构的n维拓扑流形

2)性质

微分流形 $(M,\mathfrak{F}_{m})$ 的一个开集本身就是一个微分流形，其微分结构为 $\mathfrak{F}_{U}=\left \{ (U_{a}\cap U,\varphi _{a}|_{U{a}\cap U})|(U_{a},\varphi _{a})\in \mathfrak{F}_{M} \right \}$ 。

设 $(M_{1},\mathfrak{F}_{1})$ 与 $(M_{2},\mathfrak{F}_{2})$ 分别为 $d_{1}$ 与 $d_{2}$ 维的微分流形，则积流行的 $M_{1}\times M_{2}$ 为 $d_{1}+d_{2}$ 的微分流形，其微分结构是

$\left \{ (U_{a}\times V_{\beta },\phi _{a}\times \psi _{\beta })|(U_{a},\phi _{a})\in\mathfrak{F}_{1},(V_{\beta },\psi _{\beta })\in\mathfrak{F}_{2} \right \}$

3)例子

一般线性群 $GL(n,\mathbb{R})$ 以行列式为 $\mathbb{R}^{n^{2}}$ 上的连续函数，则 $GL(n,\mathbb{R})$ 作为 $\mathbb{R}^{n^{2}}$ 的开集，是一个微分流形

②来自[美国]弗兰克·W·瓦内尔的《数学名著译丛书-微分流形与李群基础》

        1.2定义        令 $U\subset \mathbb{R}^{d}$ 是开集，并且令 $f:U\rightarrow \mathbb{R}$ .k是一个非负整数，如果对于 $[a]\leqslant k$ ，各偏导数 $\frac{\partial ^{\alpha}f}{\partial r^{\alpha }}$ 存在且在U上连续，则称f在U上是 $C^{k}$ 类可微的（或简称f是 $C^{k}$ 的）。特别地，若 $f$ 是连续的，则发 $f$ 是 $C^{0}$ 的，若果 $f:U\rightarrow \mathbb{R}^{n}$ ，那么，若每个分量函数 $f_{i}=r_{i} {}^{\circ}f$ 为 $C^{k}$ 的，则 $f$ 是 $C^{k}$ 类可微的，如果 $f$ 对所有 $k\geqslant 0$ 是 $C^{k}$ 的则称 $f$ 是 $C^{\infty }$

        1.3定义        一个d维局部Euclid空间 $M$ 是一个Hausdorff拓扑空间 $M$ ，而且它的每一个点都有一个邻域同胚于Eucild空间 $\mathbb{R}^{d}$ 的一个开集。如果 $\varphi$ 是连通开集 $U\subset M$ 到 $\mathbb{R}^{d}$ 的原点为中心的开立方体，则把坐标系 $(U,\varphi )$ 称为立体坐标系，如果 $m \in U$ 且 $\varphi(m)=0$ ，则称该坐标系是m为中心的

        1.4定义        局部eucild空间M上的一个 $C^{k}$ 类 $(1\leqslant k \leqslant \infty )$ 可微结构 $\mathfrak{F}$ 是满足下列三个性质的一族坐标系 $\left \{ (U_{\alpha },\varphi _{a}):\alpha \in A \right \}:$

        (a) $\bigcup_{\alpha \in A} U_{\alpha }=M$

        (b) $\varphi _{a}{}^{\circ}\varphi _{\beta }^{-1}$ 对于所有 $\alpha ,\beta \in A$ 是 $C^{k}$ 的

        (c)集族 $\mathfrak{F}=\left \{ (U_{a},\varphi _{a}):a\in A \right \}$ 是满足性质(a)和性质(b)的任何一个坐标系族，那么存在唯一一个包含 $\mathfrak{F}_{0}$ 的可微结构 $\mathfrak{F}$ ，即令

$\mathfrak{F}$ ={ $(U,\varphi)$ :对于所有 $\varphi_{a}\in \mathfrak{F},\varphi ^{\circ}\varphi_{a}^{-1}$ 是 $C^{k}$ 的}

那么 $\mathfrak{F}$ 包含 $\mathfrak{F}_{0}$ ，显然(a)满足，并且容易验证 $\mathfrak{F}$ 满足(b),因为由构造可以知道， $\mathfrak{F}$ 是极大地，所以 $\mathfrak{F}$ 是包含 $\mathfrak{F}_{0}$ 的一个可微结构，显然他是唯一的这种结构。

        下面提到的局部Eucild空间上另外两种基本类型的可微结构，这就是 $C^{\omega }$ 类结构和复解析结构，但本书中并不处理这两种类型，对于 $C^{\omega }$ 类可微结构来说，要求(b)中的复合映射能够局部的由收敛幂级数给出，对于2d维局部Euclid空间上的复解析结构，则要求坐标系的值域在d维复空间 $\mathbb{C}^{d}$ 中并且使全纯的相互交叠。

这些使一些关于微分结构的定义，而微分流形就是具有微分结构的拓扑流形。

三：子流行

①来自百度和知乎上的定义和相关概念

子流行是单浸入映射对应的流形见得关系。设 $M,N$ 是两个微分流形， $\varphi :M\rightarrow N$ 是 $C^{\infty}$ 映射，若 $\varphi$ 是单射，且 $\varphi$ 是浸入，则称 $(M,\varphi )$ 的 $N$ 的子流行，也可以等价定义为， $M$ 作为点集 $N$ 的子集，且从 $M$ 到 $N$ 的恒等映射是 $M$ 到 $N$ 中的嵌入，就称 $M$ 为 $N$ 的子流形

子流行，显然和子集有关系，由上还有N为微分结构和拓扑结构都是由M上的相对应的结构限制而得到

②来自[法国]贝尔热和戈斯丢的《法兰西数学精品译丛04-微分几何：流形、曲线和曲面》的定义和相关概念

2.1 $R^{n}$ 的子流形

        对于 $d\leqslant n$ ，典型包含 $R^{d}\subset R^{n}$ 是映射 $(x_{1},x_{2},...x_{d})\mapsto (x_{1},...,x_{d},0,...,0)$ ，这也可以表示成为 $R^{n}=R^{d}\times R^{n-d}$

        2.1.1定义

        给定 $R^{n}$ 的一个子集V。我们称V是 $R^{n}$ 的d维 $C^{p}$ 类的子流行，如果对于V的每一个点 $x$ ,存在 $R^{n}$ 的一个含有点 $x$ 的开集 $U$ 到其像 $f(U)$ 的 $C^{p}$ 类的微分同胚 $f$ ( $f(U)$ 是 $R^{n}$ 的开集)，满足条件: $f(U\cap V)=f(U)\cap R^{d}$ .n-d称为V的余维度。

2.6子流形，浸入，浸没，嵌入

        现在把2.1的子流形概念从 $R^{n}$ 推广到抽象流形，读者应当用心画出有关的图形，一边加深对于概念的理解

        2.6.1 定义

        设X是一个d维流形，而Y是X的一个自己，我们说Y是X的e维子流行，如果对于Y的每个y，存在X的一个在y的坐标卡 $(U,\varphi)$ ，使得 $\varphi(U\cap Y)=\varphi(U)\cap R^{e}$

        这里利用典范包含映射

$R^{e}\rightarrow R^{e}\times \left \{ 0 \right \}\subset R^{e}\times R^{d-e}=R^{d}$

把 $R^{e}$ 等同于 $R^{e}\rightarrow R^{e}\times \left \{ 0 \right \} \subset R^{e}\times R^{d-e}=R^{d}$

        如Y在X内的状态处处局部地微分同胚于 $R^{e}$ 在 $R^{d}$ 内的状态，则Y是X的子流形

这些例子给我们展示了对于所有的 $\varepsilon \in \mathbb{R}-\left \{ 0 \right \}$ 的解的图像在拓扑角度看来总是一个曲面， $X^{(\varepsilon )}\subseteq \mathbb{R}^{4}$ 的实部 $X^{(\varepsilon )}_{\mathbb{R}}$ 是通过实平面 $y_{1}=y_{2}=0$ 的切片而产生的，也就是说 $X^{(\varepsilon )}_{\mathbb{R}}$ 的样子是不取决于 $X^{(\varepsilon )}$ 的拓扑形状的，而是取决于 $\mathbb{R}^{4}$ 空间内的情况。显然对于 $\varepsilon >0$ 时候， $X^{(\varepsilon )}_{\mathbb{R}}$ 是一个圆，而 $X^{(-\varepsilon )}_{\mathbb{R}}$ 是空的。在几何学上有一个解释， $X^{(-\varepsilon )}$ 是通过旋转 $\tau$ 从 $X^{(\varepsilon )}_{\mathbb{R}}$ 中出现，并且在旋转之后不会出现在真是的平面之中。

我们可以甚至可以更进一步，可以将 $X^{(\varepsilon )}=V(z_{1}^{2}+z_{1}^{2}-\varepsilon )$ 看成任意的 $\varepsilon \in\mathbb{C}$ ，设 $\varepsilon \neq 0$ ，所以我们选择 $\delta \in \mathbb{C}$ ，以便于我们观察和研究映射 $\sigma :$ 通过 $(z_{1},z_{2})\mapsto (\delta z_{1},\delta z_{2})$ 定义的 $\mathbb{C}^{2}\rightarrow \mathbb{C}^{2}$ . $\sigma$ 是一个同胚，并且有关系： $\sigma (X^{(1)})=X^{(\varepsilon )}$ 。所以 $X^{(\varepsilon )}$ 一直同胚与 $X^{1}$ 。 $X^{(\varepsilon )}$ 的性状和几乎所有的 $\varepsilon \in \mathbb{C}-\left \{ 0 \right \}$ 的形状相同，即 $H^{(1)}$ 。因此， $X^{(\varepsilon )}$ 的形状也是几乎对于所有 $\varepsilon \in \mathbb{C}$ 是同样的。这满足了一个经典的代数几何学理论：也就是所谓的“持久性原则”（后文看的出来是“连续性”的意思），意思就是说， $V(\left \{ f_{i} \right \})$ 的根的图像的几何性质是几乎是相同的，当其定义多项式的系数 $f_{i}$ 变化的时。人们很容易看出来，解的图像的性质可以随着性质的变化而变化，当人们观察 $X^{(\varepsilon )}$ , $\varepsilon =0$ 的时候，由于 $(z_{1}^{2}+z_{2}^{2}=(z_{1}+iz_{2})(z_{2}-iz_{1}))$ 关系到 $X^{(0)}=V(z^{2}_{1}+z^{2}_{2})=V(z_{1}+iz_{2})\cup V(z_{1}-iz_{2})$ 。在 $\mathbb{R}^{4}$ 空间中，可以知道 $V(z_{1}+iz_{2})$ 和 $V(z_{1}-iz_{2})$ 这两个平面在原点上有一个交点.所以从拓扑上来说， $X^{(0)}$ 对应于两个横向相交平面的并集，所以它必然不与 $H^{(1)}$ 同胚。

那么事实就是，对于所有的 $\varepsilon <0$ 时的 $X^{(\varepsilon )}_{\mathbb{R}}$ ，很明显的在实数范围内违背了持久性原则/持续性原则

注意：持久性（也就是连续性），以上的这些表达实际上是不连续的，至少如半连续性，这些东西并没能在这些话中表达出来。

博主注：

1.连续

连续是一种数学属性，常用的连续性的最根本的定义是在拓扑学中德定义，在条目连续函数中（拓扑学）有详细描述，在序理论，特别是阈理论中，有从这个基础概念中得出的另一种抽象的连续性，斯科特连续性

①实值连续函数（无间断，跳跃或无限逼近的震荡）

严格来说，设 $f$ 是一个从实数集的子集 $I\subset \mathbb{R}$ 映射到了 $J\subset \mathbb{R}$ 的函数： $f:I\rightarrow J$ , $f$ 在 $I$ 中的某一点c处是连续的，当且仅当一下两个条件的满足：

1） $f$ 在 $c$ 上有定义

2） $c$ 是 $I$ 中的一个聚点，并且无论自变量 $x$ 在 $I$ 中以什么方式接近 $c$ ， $f(x)$ 的极限都存在并且等于 $f(c)$

②定义

不用极限的概念，使用 $"\varepsilon -\delta "$ 的方法

考虑 $f:I\rightarrow J$ ，设 $c$ 为 $f$ 定义域中的一个元素，函数 $f$ 被称为在 $c$ 点连续当且仅当以下条件成立：

对于任意的正实数 $\varepsilon>0$ ，存在一个正实数 $\delta >0$ 使得，对于任意定义域中的 $x \in I$ ，只要 $x$ 满足 $c-\delta <x<c+\delta$ 就有 $f(c)-\varepsilon <f(x)<f(c)+\varepsilon$

③半连续性

半连续性分为上半连续和下半连续

上半连续：设 $x$ 为拓扑空间， $x_{0}\in X$ ，而 $f:X\rightarrow \mathbb{R}$ 为实值函数，若对每个 $\varepsilon >0$ 都存在 $x_{0}$ 的开邻域 $U$ 使得 $\forall x\in U$ , $f(x)<f(x_{0})+\varepsilon$ 则 $f$ 在 $x_{0}$ 上半连续，也可表示为：

$lim_{x\rightarrow x_{0}}f(x)\leqslant f(x_{0})$

下半连续：设 $x$ 为拓扑空间， $x_{0}\in X$ ，而 $f:X\rightarrow \mathbb{R}$ 为实值函数，若对每个 $\varepsilon >0$ 都存在 $x_{0}$ 的开邻域 $U$ 使得 $\forall x\in U$ , $f(x)>f(x_{0})+\varepsilon$ 则 $f$ 在 $x_{0}$ 上半连续，也可表示为：

$lim_{x\rightarrow x_{0}}f(x)\geqslant f(x_{0})$

好的，那么这就是我们大致的内容了，但是请问我们结束了吗？

显然没有，既然说都说了这么多了，不妨再多说一些

知识拓展：

1.微分同胚

微分同胚是适用于微分流形范畴的同构概念，这是从微分流形之间的可逆映射，使得此映射其逆映射均为光滑（即无穷可微）德。

①定义

对于给定的两个光滑流形 $M$ 与 $N$ ，若 $f:M\rightarrow N$ 为双射，且 $f$ 与 $f^{-1}$ 均为光滑映射，则称 $f$ 为微分同胚

②性质+相关概念

$M$ 上所有的微分同胚集 $Diff(M)$ 在符合映射下为群

如果微分流形 $M$ ， $N$ 之间存在微分同胚映射，那么称 $M$ ， $N$ 是微分同胚的

2.张量和张量积

①来自百度的关于张量的概念

张量是矢量这一概念的推广，矢量是一阶张量，张量是一个可用来表示在一些矢量，标量和其他张量之间的线性关系的多线性函数

张量是一个定义在一些向量空间和一些对偶空间的笛卡尔积上的多重线性映射，其坐标是 $|n|$ 维空间内，有 $|n|$ 个分量的以重量

一：一些规定

1）求和约定

指在给定的项中凡有一上和一下两个相同的指标就表示对该指标从1到空间维数N求和，例如在三维空间中， $a_{i}x^{i}=a{i}x^{1}+a_{2}x^{2}+a_{3}x^{3}$

2）张量指标

包括哑指标和自由指标，哑指标是指各项中一上和一下成对的相同指标，例如，上式中的指标就是哑指标，自由指标是指在方程的所有项中只出现过一次的指标

二：定义

有两种定义张量的方法：

1）按变换规律定义

若一个坐标系 $\left \{ x^{i} \right \}$ 中 $N^{r+s}$ 个量 $T^{i_{1},i_{2},...,i_{r}}_{j_{1},j_{2},...,j_{r}}$ 与另一个坐标系 $\left \{ x^{i^{'}} \right \}$ 中 $N^{r+s}$ 个量 $T^{i_{1'},i_{2'},...,i_{r'}}_{j_{1'},j_{2'},...,j_{r'}}$ 满足交换律

$T^{i_{1'},i_{2'},...,i_{r'}}_{j_{1'},j_{2'},...,j_{r'}}=\frac{\partial x^{i1'}}{\partial x^{i1}}...\frac{\partial x^{ir'}}{\partial x^{ir}}\frac{\partial x^{j1}}{\partial x^{j1'}}...\frac{\partial x^{js}}{\partial x^{js'}}T^{i_{1}...i_{r}}_{j_{1}...j_{s}}$

则 $T^{i_{1}...i_{r}}_{j_{1}...j_{s}}$ 成为r1阶逆变和s阶协变混合张量的分量，若s=0,则 $T^{i_{1}...i_{r}}$ 称为r阶逆变张量的分量，若r=0,则 $T_{j_{1}...j_{s}}$ 称为s阶协变张量的分量，商住张量记发称之为分量记发。

2）按照不变性定义

凡可以在任何坐标系中写成下列不变性形式的量定义为r+s阶张量

$T=T^{i_{1},i_{2},...,i_{r}}_{j_{1},j_{2},...,j_{r}}g_{i1}...g_{ir} g^{j1}...g^{js}=T^{i_{1'},i_{2'},...,i_{r'}}_{j_{1'},j_{2'},...,j_{r'}}g_{i1'}...g_{ir'} g^{j1'}...g^{js'}$

式中 $g_{i}(g^{j})$ 和 $g_{i'}(g^{j'})$ 分别为坐标系 $\left \{ x^{i} \right \}$ 和 $\left \{ x^{i'} \right \}$ 中的协（逆）变基矢量，上述这种张量记法称为不变形记法或并矢记法

②来自百度的关于张量积的概念

张量积可以用在不同的东西上，如向量，矩阵，张量，向量空间，代数，拓扑向量空间和模。

一：多种张量积

在这里我们就主要讲比较简单的一些，如两个张量的张量积，多重线性映射的张量积，就不会去提到向量空间的张量积，希尔伯特空间的张量积，这个在我们后面讨论线性运算的时候可以说一说，这里只是代数几何的相关概念的拓展

1）两个张量的张量积

有两个或更多张量积的分量的一般公式，例如，比如 $U$ 和 $V$ 是秩分别为n何m的两个协变张量，则它们的张量积给出为

$(V\bigotimes U)_{i_{i},i_{2,...,i_{m+n}}}=V_{i_{1},i_{2},i_{3},...,i_{n}}U_{i_{n+1},i_{n+2},...,i_{n+m}}$

所以两个张量的张量积的分量是每个张量的分量的普通积

主义在张量积中，因子 $U$ 消耗一个 $rank(U)$ 指标，而因子 $V$ 消耗下一个 $rank(V)$ 指标，所以 $rank(U\otimes V)=rank(U)rank(V)$

2）多重线性映射的张量积

$f(x_{1},...,x_{k})$ 给定多重线性映射和 $g(x_{1},...x_{m})$ 他们的张量积是多重线性函数 $(f\bigotimes g)(x_{1},...,x_{k+m})=f(x_{1},...,x_{k})g(x_{k+1},...,x_{k+m})$

二：例子

$b\otimes a\rightarrow \begin{bmatrix} b_{1}\\ b_{2}\\ b_{3}\\ b_{4}\\ \end{bmatrix} \begin{bmatrix} a_{1} & a_{2} & a_{3} \end{bmatrix}=\begin{bmatrix} a_{1}b_{1} &a_{2}b_{1} &a_{3}b_{1} \\ a_{1}b_{2} &a_{2}b_{2} &a_{3}b_{2} \\ a_{1}b_{3} &a_{2}b_{3} &a_{3}b_{3} \\ a_{1}b_{4} &a_{2}b_{4} &a_{3}b_{4} \end{bmatrix}$

结果的秩为1，结果的维数为 $4\times 3=12$

这里的秩指示张量秩（所需指标数），二维度解散在结果数组中自由度的数目；矩阵的秩是1

代表情况是任何两个被当做矩阵的矩形数组的的克罗内克积，在同维数的两个向量之间的张量积的特殊情况是并矢积。

3.张量代数（入门）

        设 $F$ 为一数域（实数域 $R$ 或复数域 $C$ ）， $V$ 为数域 $F$ 上一个n维矢量空间，映射 $f:V\rightarrow F$ 为一线性泛函，即对任何 $v_{1},v_{2}\in V$ 和任何 $\alpha ,\beta\in F$ ，等式

$f(\alpha v_{1}+\beta v_{2})=\alpha f(v_{1})+\beta f(v_{2})$

恒成立， $V$ 上一切具有这种性质的线性泛函的集合记作 $V^{*}$ ，称为 $V$ 的对偶空间，在 $V^{*}$ 上也可定义加法以及和 $F$ 中数的乘法：对任何 $f,g\in V^{*}$ ，对于任何 $v\in V$ 与任何 $\alpha \in F$ ，恒有

$(f+g)(v)=f(v)+g(v),$

$(af)(v)=af(v)$

于是 $V^{*}$ 变成数域 $F$ 上的一个矢量空间（也可以称之为线性空间）

        命 $[e_{1},e_{2},...,e_{n}]$ 表示一个矢量空间 $V$ 的一个基，显然 $V$ 上一个线性泛函 $f$ 可由它在 $e_{1},...,e_{n}$ 上的值决定，例如对任何

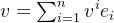
$v=\sum_{i=1}^{n}v^{i}e_{i}$    $(v^{i} \in F)$

有

$f(v)=\sum_{i=1}^{n}v^{i}f(e_{i})$

假如我们定义 $V^{*}$ 中n个元素 $f^{1},f^{2},...,f^{n}$ ，使

$f^{i}(e_{j})=\delta ^{i}_{j}=\left\{\begin{matrix} 1, when & i=j,\\ 0,when & i\neq j, \end{matrix}\right.$

这里 $i,j=1,2,...,n.$ 于是 $f^{1},f^{2},...,f^{n}$ 是线性独立的，事实上，若在 $F$ 中存在n个数 $l_{1},l_{2},...,l_{n}$

使                                          $l_{1}f^{1}+l_{2}f^{2}+...+l_{n}f^{n}=0,$

自然等式 $0=(\sum_{j=1}^{n}l_{j}f^{j})(e_{i})=\sum_{j=1}^{n}l_{jf^{j}(e^{j})}=\sum_{j=1}^{n}l_{j}\delta _{i}^{j}=l_{i} ,$

对于每一个 $i=1,2,...,n$ 成立，另一面，任意取 $f \in V^{*}$ ，命 $f(e_{i})=a_{i}$ ，则

$(f-\sum _{i=1}^{n}a_{i}f^{i})(e^{j})=f(e_{j})-\sum_{i=1}^{n}a_{i}f^{i}(e_{j})=a_{j}-a_{j}=0$

其中 $j=1,2,...,n$ 从而 $f=\sum _{i=1}^{n} a_{1}f^{i}$ 。这说明 $f^{1},f^{2},...,f^{n}$ 是空间 $V^{*}$ 的一个基，从而 $dimV^{*}=n$ ，由于 $f^{i}(e_{j})=\delta _{j}^{i}$ ，我们称 $[f^{1},...,f^{n}]$ 是 $[e_{1},...,e_{n}]$ 的对偶基(dual base)，记住他们分别为 $V^{*}$ 和 $V$ 的基。

既然 $V^{*}$ 是 $F$ 上的一个矢量空间， $V^{*}$ 的对偶空间 $(V^{*})^{*}$ 应该仍是 $F$ 上的一个n维线性空间，我们要在 $V$ 和 $(V^{*})^{*}$ 之间建立一个同构关系，将 $v\in V$ 对应于 $(V^{*})^{*}$ 中的一个元素 $v^{**}$ ，其定义是：对于任何 $f \in V^{*}$ ，有 $v^{**}(f)=f(v)\in F$

这样定义的 $v^{**}$ 确是 $V^{*}$ 上的一个线性泛函，对应 $\phi :v \mapsto v^{**}$ 是一个单射，事实上，若 $v_{1} \mapsto v_{1}^{**},v_{2} \mapsto v_{2}^{**}$ 有 $v_{1}^{**}=v_{2}^{**}$ ，则对任何 $f \in V^{*}$ ，有

                                                 $0=v_{1}^{**}(f)-v_{2}^{**}(f)$

          $=f(v_{1})-f(v_{2})=f(v_{1}-v_{2})$

命 $v_{1}-v_{2}=\sum _{i=1}^{n}l_{i}e_{i}$ ，取底矢量 $f^{i}\in V^{*}$ ，要求 $[f^{1},...,f^{n}]$ 为 $[e_{1},...,e_{n}]$ 的对偶基，则

$0=f^{j}(\sum _{i=1}^{n}l_{i}e_{i})=\sum_{i=1}^{n}l_{i}f^{i}(e_{i})=l_{j},$

其中 $j=1,2,...,n,$ 从而 $v_{1}-v_{2}=0$ ，这就肯定了映射 $\phi$ 是单射，可是 $dimV^{**}=n=dimV$ ，因此，映射 $\phi$ 必是满射，从而 $\phi$ 在 $V$ 与 $V^{**}$ 之间建立一个同构对应，我们不妨就此把 $V$ 与 $V^{**}$ 等同起来，从而 $V$ 也是 $V^{*}$ 的对偶空间，这样的约定将给后面的论述带来许多方便，当 $v\in V$ , $f \in V^{*}$ ，数 $f(v)$ 也常写作 $<f,v>$ ，并称运算符 $<,>$ 为 $V$ 与 $V^{*}$ 的配对（pairing），采用这种写法，更能体现两个矢量空间 $V$ 和 $V^{*}$ 的对偶性。

        下面引进多重线性映射的概念。若 $V_{1},V_{2},...,V_{r},Z$ 为 $F$ 上 $r+1$ 个有限维线性空间，我们说泛函 $f:V_{1}\times V_{2}\times ...\times V_{r} \rightarrow Z$ 是r重线性的，意味着，任意取 $v_{i}\in V_{i}(i=1,2,...,r)$ ，函数关系

$f(v_{1},v_{2},...,v_{r})\in Z$

对每一个变量 $v_{i}(i=1.2....,r)$ 都是线性的，

        一切这样的线性映射的集合记作

$\Psi (V_{1},V_{2},...,V_{r};Z)$

当然 $\Psi (V_{1},V_{2},...,V_{r};Z)$ 也可看做是数域 $F$ 上的一个线性空间，特别在 $Z=F$ （1维线性空间）时候，我们称呼上面定义的 $f$ 为多重线性函数。

        若 $dimV_{i}=n_{i}(i=1,2,...,r)$ ，取 $V_{i}$ 的一个基 $[e_{i_{1}},e_{i_{2}},...,e_{ni}]$ ，在 $\Psi (V_{1},V_{2},...,V_{r};F)$ 中取元素

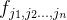
$f_{j_{1},j_{2}...,j_{n}}$          $(j_{i}=1,2,...,n;1\leqslant i\leqslant r),$

其定义为 $f_{j_{1},j_{2},...,j_{r}}(e_{1i_{1}},e_{2i_{2}},...,e_{ri_{r}})=\delta _{i_{1}}^{j_{1}} \delta _{i_{2}}^{j_{2}}...\delta _{i_{r}}^{j_{r}}$ ，则不难验证 $[f_{j_{1},j_{2},...,j_{r}}|1\leqslant j_{i}\leqslant n_{i},1\leqslant i\leqslant r]$ 构成线性空间 $\Psi (V_{1},V_{2},...,V_{r};F)$ 的一个基，所以 $dim\Psi (V_{1},V_{2},...,V_{r};F)=n_{1}n_{2}...n_{r}=(dimV_{1})(dimV_{2})...(dimV_{r})$

非常抱歉这一篇文章只能写道这里为止，博主已经到德国，但是，这边的网络不太好，本来博主还想讲很多，简单列举一下吧：

1.黎曼流形

2.伪黎曼流形

3.连续统

4.切空间

5.切向量

6.积流形

7.列维奇维塔联络

8.光滑映射

9.外代数

10.向量的代数计算

11.向量的微分计算

12.Frobenius定理

13.第二可数公理

这些，但是博主觉得不能再拖延了，这些内容我们可以放到后面去讲，很多已经和代数几何没有关系了，很多纯粹就是数学分析，拓扑，微分几何，抽象代数之类的东西了，总之都是一些近世数学或者现代数学的内容了，关于数学分析，我们可以根据吉米多维奇的数学分析来提前做一下，联系一下，吉米多维奇是上世纪从苏联引进的一本非常好的教材，尽管稍微老了一些，但是依旧非常有含金量，题目也不简单。好吧，就这么多吧——写于德国汉堡Radissonblu酒店，当地时间凌晨2:36

资料来源：

网站：

1.n维欧几里得空间_百度

2.同态_百度

3.同胚_百度

4.同构_百度

5.同伦_百度

6.1.2 Homomorphism and Isomorphism(同态与同构) - 知乎——Nick Yin视频

7.代数拓扑中的同调和上同调有哪些联系？ - 知乎——Yan Z的回答

8.流形_百度

9.微分流形_百度

10.子流行_百度

11.推荐的一篇同调的文章：同调 - 知乎

12.豪斯道夫空间_百度

13.拓扑空间_百度

14.Hausdorff空间_中文数学wiki，Fandom网站
15.坐标卡：一般微分几何：坐标与流形 - 知乎

16.豪斯多夫空间基本概念，性质，定理 - 知乎

17.拓扑学入门1——拓扑空间 - 知乎

18.半连续性（Semi-continuous） - 知乎

19.连续_百度

20.一般微分几何：坐标与流形 - 知乎

21.微分流形（一） - 知乎

22.微分流形_百度

23.微分同胚_百度

24.子流行_百度

25.一般微分几何：子流形 - 知乎

26.柯尔莫果洛夫空间_百度

27.紧空间_百度

28.弱豪斯道夫空间_百度

29.同调_百度

30.坐标卡_百度

31.局部坐标系_百度

32.正规空间_百度

等等等，不想列了，太多了。

书籍：

1《代数几何导引（德文版）》——[瑞士] 马库斯·布罗德曼，哈尔滨工业大学出版社

2.《法兰西数学精品译丛04-微分几何：流形、曲线和曲面》——[法国]贝尔热，戈斯丢，高等教育出版社

3.《数学名著译丛书-微分流形与李群基础》——[美国]弗兰克·W·瓦内尔，科学出版社

4.《微分几何初步》——陈维恒

5.《流形的拓扑学》——苏况存，武汉大学出版社

6.《流形和微分几何初步》——梅加强，科学出版社

7.《微分流形与黎曼几何》——梅向明，北京师范学院出版社

8.《微分几何讲义》——陈省身，世界图书出版社

9.《微分几何的理论和问题》——杨文茂，江西教育出版社

10.《微分几何导引》——黄正中，南京大学出版社

11.《微分几何习题集》——[苏联]А.С.ФЕДЕНКО，苏联科学出版社

12.《拓扑学的首要概念》——[美国]陈锡驹，斯廷路德，上海科学技术出版社