拓扑数据分析-Topological data analysis

最新推荐文章于 2023-12-27 21:44:12 发布

Xiaofei@IDO

最新推荐文章于 2023-12-27 21:44:12 发布

阅读量1w

点赞数 4

分类专栏：机器学习文章标签：数据分析数据挖掘机器学习

本文链接：https://blog.csdn.net/nixiang_888/article/details/122366290

版权

机器学习专栏收录该内容

8 篇文章

订阅专栏

拓扑数据分析（TDA）结合了拓扑学与数据分析，用于揭示复杂高维数据中的拓扑信息和形状特征。Mapper算法是TDA中的关键步骤，通过滤波、覆盖、聚类和构建拓扑图来捕获数据的不变性质。这种方法能够发现传统方法无法识别的小规模结构，并且保持信息的鲁棒性。在Python中，可以使用如GUDHI、scikit-tda或Giotto等库来实现TDA，Giotto是一个与scikit-learn兼容的库，适用于机器学习和高效性能的拓扑分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、拓扑概念

拓扑主要研究的对象为几何图形或空间结构，探究在连续改变形状后还能保持不变的一些性质。它只考虑物体间的位置关系而不考虑它们的形状和大小。简单的描述为：一些特殊的几何性质，在图形连续改变形状后还能继续保持不变。

二、拓扑数据分析

拓扑学研究的是一些特殊的几何性质，这些性质在图形连续改变形状后还能继续保持不变，称为“拓扑性质”。而在复杂的高维数据内部也存在着类似的结构性质，我们可以形象地称之为数据的形状（特征）。

拓扑数据分析(Topological data analysis, TDA)，顾名思义，就是把拓扑学与数据分析结合的一种分析方法，用于深入研究大数据中潜藏的有价值的关系。

相比于主成分分析、聚类分析这些常用的方法，TDA不仅可以有效地捕捉高维数据空间的拓扑信息，而且擅长发现一些用传统方法无法发现的小分类。这种方法也因此曾在基因与癌症研究领域大显身手。
和通常研究的成对关系相比，这种相互关系的形状之中可能潜藏了巨大的研究价值。要理解数据的形状，就必须求助于拓扑学。TDA所做的就是抽取这种形状并进行分析。

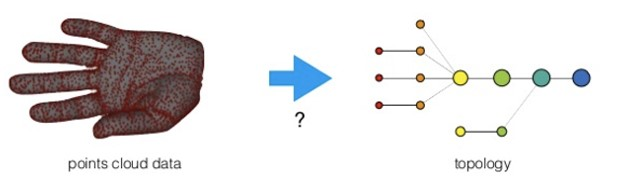
三、拓扑分析步骤

在TDA数据分析中，mapper算法是必须的。具体的实现过程如下。

数据矩阵

输入数据：输入数据可以是任何类型的数据，但是要满足一定的条件，即输入的数据必须要能够计算任何两数据之间的距离（这距离不局限于欧几里得距离，可以是用户定义的一些距离公式，目的就是要能够确定这个数据在总的输入数据中的一个大致“位置”）。
输出：一个关于输入数据的拓扑图。

Mapper算法

The Algorithm
Given a dataset of points, the basic steps behind Mapper are as follows:

Map to a lower-dimensional space using a filter function $f$ , or lens. Common choices for the filter function include projection onto one or more axes via PCA or density-based methods.
Construct a cover $(U_i)_{i\in I}$ of the projected space typically in the form of a set of overlapping intervals which have constant length.
For each interval U_i cluster the points in the preimage $f^{-1}(U_i)$ into sets $C_{i,1},\ldots,C_{i,k_i}$ .
Construct the graph whose vertices are the cluster sets and an edge exists between two vertices if two clusters share some points in common.

使用一个（或多个）filter 函数，将输入数据X经过计算得到一个（或多个）值。即f(X) = a ，a是一个实数。
设置两个超参，分别是resolution（即intervals的间距大小）和overlap（重叠区间的大小）。（重要！！）
在每个intervals里面进行局部聚类，可以使用任何聚类算法。将聚在一起的类归并到一个拓扑节点。每一个拓扑节点中包含了不同的数据点。
基于第2步，resolution中设置的overlap（相邻intervals里面会有公共的数据点），将有overlap的两个拓扑节点，使用线连接起来。

优点

优点1：一般现有的算法，如果要对高维数据进行可视化，必然会有一个降维的过程，那么现有的算法在降维后对原始数据会有一些信息的损失（维数越高，越明显）。而mapper算法始终保留高维空间中数据的整体拓扑信息，在这个方面，它远胜于其他算法。
优点2：能够发现一些更小的类，检测传统方法无法找到的集群和有趣的拓扑结构
优点3：发现的特征具有鲁棒性，选择最能区分数据和模型可解释性的特征

基于python的实现

Nowadays there are a few python open source libraries implementing the main TDA tools, like GUDHI, scikit-tda and Giotto. For our test we chose to use one of the most recent: the Giotto library, which is scikit-learn compatible, oriented towards machine learning, fast-performing with C++ state-of-the-art implementations.

# Define filter function
filter_func = umap.UMAP(n_neighbors=5) 
# Define cover
cover = CubicalCover(kind='balanced', n_intervals=10, overlap_frac=0.2)
# Choose clustering algorithm 
clusterer = DBSCAN(eps=10)
# Initialise pipeline
pipe = make_mapper_pipeline(
    filter_func=filter_func,
    cover=cover,
    clusterer=clusterer,
    verbose=True,
    n_jobs=-1,
)
# Plot Mapper graph
fig = plot_static_mapper_graph(pipe, X, color_by_columns_dropdown=True, color_variable=y)
fig.show(config={'scrollZoom': True})