台大林轩田机器学习课程笔记3----机器学习的可行性

原文地址： http://blog.csdn.net/steveyinger/article/details/51171828

引例

先引入一个矛盾问题： 
 

图3.1 图案学习问题
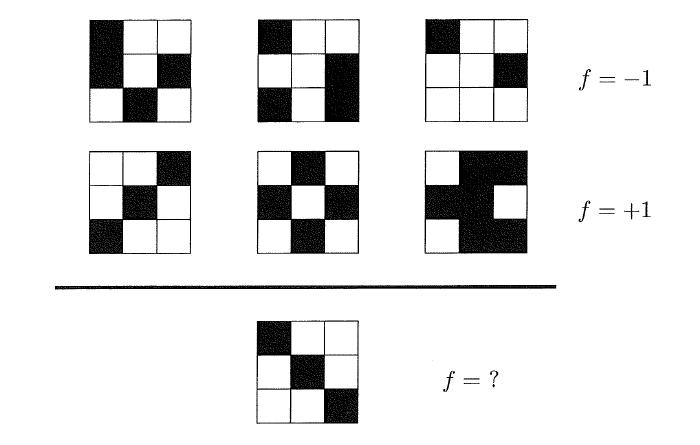
这是一道推理题，根据第一行和第二行图形的规律分别输出-1和+1，然后通过上述规则学习推理出第三行图形的输出。每个人通过学习所获得的答案是会不一致的，例如通过对称的规律可以得到第三行的图形f=+1，而如果通过图案左上角颜色的规律则得到第三行的图形f=-1。所以该问题没有足够的信息告诉我们哪一个是正确的答案。

学习是否可行

那么学习到底可不可行？根据图3.1，前两行就是训练数据集D,我们知道D上所有点的f值，但是由于在数据集D之外我们并没有太多关于f的信息，所以这并不意味着我们已经学习到了f。如果数据集D可以告诉我们一些D之外的事情，那么我们会学习到一些东西，否则，学习是不可行的。 
 

图3.2
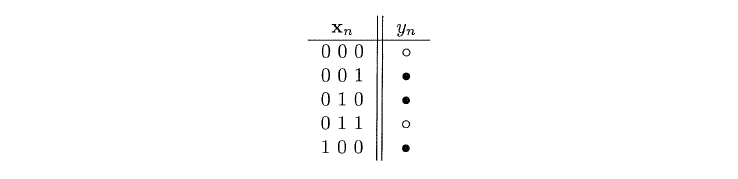
考虑一个在三维输入空间X={0,1}\^3下的布尔目标函数，如图3.2，给出了五个样本以及实心/空心输出。当然该问题的一个优势是通过穷举可以得出所有的输入以及输出。 
 
图3.3
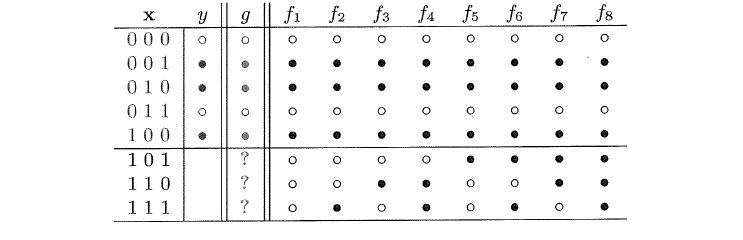
我们需要通过学习上面五个样本来推测出下面三个点的输出,即要得出最终的假设g,这里列举出了f的所有可能学习到的情况，在数据集D中的结果显而易见g=f,而在D以外的g与f的关系无法确定。但是数据集D外部g与f的关系才是我们想要的。上述这类问题我们称之为“No Free Launch”。所以综上所述，如果我们没有f的任何的信息，那么我们无法在数据集外部进行推测。

补救的办法

接下来我们将通过概率方式利用已知的数据集D去推测D外部的情况。 
 

图3.4 弹珠抽样问题
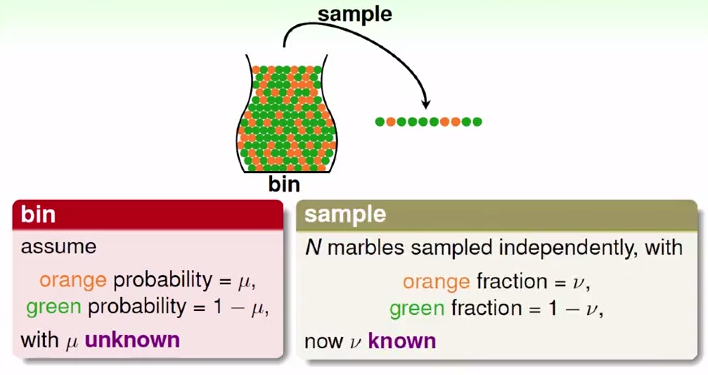
举一个简单的弹珠抽样的例子，在一个罐子里有若干弹珠，假设抽到橙色弹珠的概率是u，绿色弹珠的概率为1-u，u是未知的。先从中抽取一部分样本，橙色弹珠为v，绿色弹珠为1-v，v是已知的。那么，我们通过v可以得到u的哪些信息呢？ 
为了量化u和v之间的关系，我们引入简单的边界公式Hoeffding Inequality，即对于任意的大的样本量N，都有： 
 
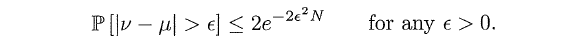
上式表明，当N越大，则v与u的差距就越小，即v与u越接近。例如丢硬币，当试验次数越来越大，则概率稳定在1/2。上式的实用性就在于，可以通过v的值来推测u的值。所以可以下结论，我们所承担的风险是“v=u is probability approximate correct(PAC)”。 
 
图3.5Hoeffding Inequality 注意事项
那么该如何将上述的弹珠示例映射到学习问题上？ 
 
图3.6 弹珠示例与学习问题的关系
首先是对于罐子里的未知数u，将其对应到学习问题上就是未知的目标函数f:X->Y。选取任一假设h将其在每个点x上与f相比较，如果h(x)=f(x)，则将点x染成绿色，否则染为红色。由于f未知，所以每个点的颜色对我们来说也是未知的。而如果根据任一概率分布P，在空间集合中随机抽取x，我们知道x有可能是红色（概率为u）也有可能是绿色（概率为1-u），这样我们就可以将学习问题与前面的弹珠问题关联起来了。其中的训练集D相当于弹珠问题的样本。 
 
图3.7 基础学习流程加入几率
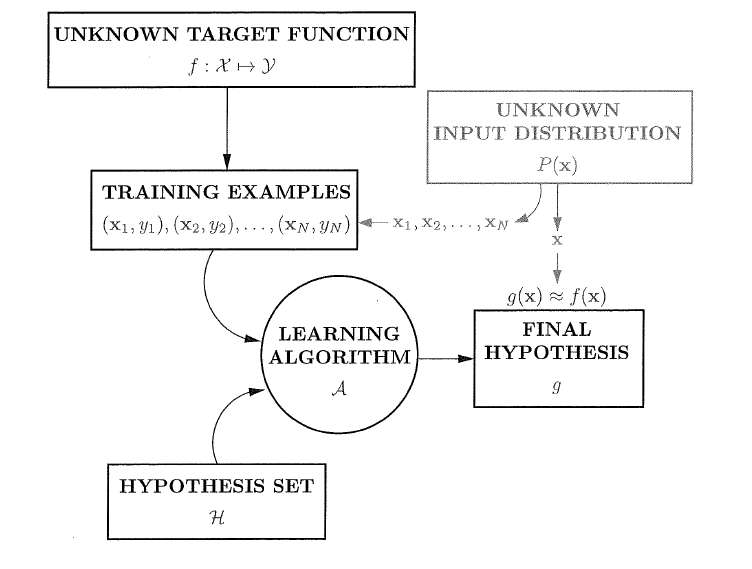
上图表示我们在原来的基础学习流程中增加了一个几率（未知的输入分布）P(x)，这个几率一方面是用来取样生成训练集，另一方面则是推断最终的假设g(x)是否与f(x)相等。这样，Hoeffding Inequality可以应用到学习问题上，且可以对数据集之外进行推测，虽然无法获知具体的f,但是会获得关于f的一些信息。 
但是现在又出现一个问题，由于v是基于一个特定的假设h，所以上文提到的抽样v是无法控制的。而在真正的学习中，我们所研究的是整个的假设集合H，然后寻找拥有尽量小错误率的一些h。我们接下来研究真正的学习，即将单一的假设拓展到多假设。

真正的学习

我们现在引入两个符号：in-sample error与out-of-sample error 
 
 
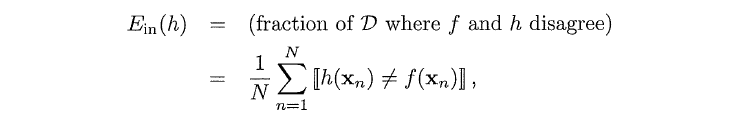
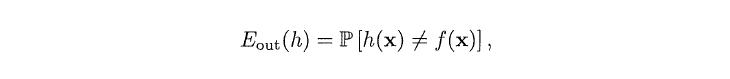
第一个公式即in-sample error，其描述的是训练数据集内的错误率，与罐子中的抽样v相对应。第二个公式即out-of-sample error，其描述的是整个概率分布P上假设h(x)是否与f(x)相等，即对应u。用两个符号分别替换u和v得到下式： 
 
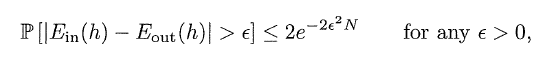
N指代训练集的数量，in-sample error是依赖样本的随机变量，out-of-sample error虽然不知道，但是不是随机的。 
接下来我们用整体的假设集合H代替单一的假设h，并且假设集合H是M个有限集合，即： 
 
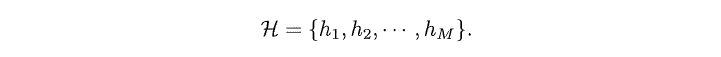
我们用罐子弹珠的示例图来描述多假设学习问题，如下图： 
 

图3.8 多罐子示例描述多假设学习问题示意图
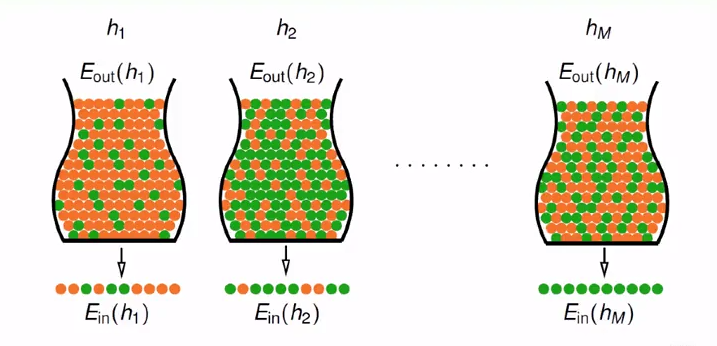
每一个罐子代表输入空间X，第M个罐子中的橙色弹珠代表的是在h(x)与f(x)不等的情况下的点x。第M个罐子中红色弹珠的概率为m-out-of-sample error,第M个样本中红色弹珠的比例为m-in-sample error。

 
 

图3.9 不好的数据集案例
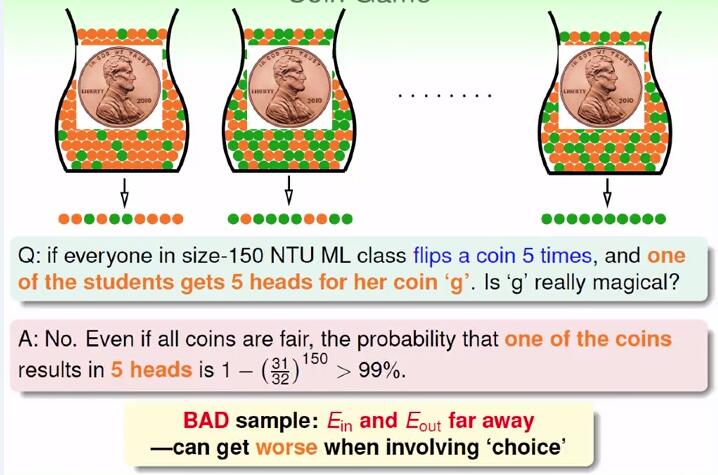
如果150个人投五次硬币，其中一个同学连续投五次正面，是否可以说明这个硬币是与众不同的。答案当然是no，因为在150次试验中，其中一枚硬币出现5次正面的概率大于99%。所以在这里E_out为1/2，E_in为0，相差很大，可以称之为不好的样本。对应到假设h上，不好的数据集就是E_out与E_in相差很远。而Hoeffding Inequality则阐述的是不好的几率非常少。 
 
图3.10 多假设集合坏数据问题
如图3.10，与多假设集合h的坏数据等价的条件包括：1、算法无法自由自在的选择数据集 2、存在h使得E_in和E_out相差很大。所以我们需要确定这M个假设集合坏数据出线几率的边界。 
 
图3.11 多假设边界推导
上式就是利用集合和概率的性质来推导出多假设坏数据集的边界，下图则是该边界式子的特点。 
 
图3.12 多假设边界的特点
根据以上公式及特点，所以在机器学习中，大多数合适的算法A挑选的都是最低的E-in的假设h来作为g。 
至此，我们就可以说，在假设集合H有限的情况下，机器学习是可行的。

参考资料： 
Coursera台大机器学习基石 
《Learning From Data》

顶

1

 

踩

0