根据《基于神经网络的短电弧覆盖次数最优化模型研究》与csdn中python拟合分析短电弧覆盖问题代码过程
一、根据论文步骤选择正n边形覆盖模型
1、最少个数正n边形覆盖计算
def find_all_n_and_x():
solutions = []
for n in range(3, 101): # 假设n的范围在3到100之间
x = 360 * n / (180 * (n - 2))
if x.is_integer() and x > 0:
solutions.append((n, int(x)))
return solutions
results = find_all_n_and_x()
if results:
print("满足条件的n和对应的x如下:")
for n, x in results:
print(f"n={n},x={x}个正{n}边形。")
else:
print("未找到满足条件的解。")
满足条件的n和对应的x如下: n=3,x=6个正3边形。 n=4,x=4个正4边形。 n=6,x=3个正6边形。
2、相邻两个内接正n边形小圆的重叠面积占整圆面积比
import math
'''球形短电弧的半径'''
r = 60.5
'''圆形材料的半径'''
R = 1000
def calculate_Ratio(n, r, R):
numerator = 2 * (1 / n * math.pi * r * r - 1 / 2 * math.sin(2 * math.pi / n) * r * r)
denominator = math.pi * r * r
Ratio = numerator / denominator
return Ratio
results = find_all_n_and_x()
if results:
print("满足条件的n和对应的Ratio如下:")
for n, x in results:
Ratio = calculate_Ratio(n, r, R)
print(f"n={n},Ratio={Ratio:.5f}")
else:
print("未找到满足条件的解。")
满足条件的n和对应的Ratio如下: n=3,Ratio=0.39100 n=4,Ratio=0.18169 n=6,Ratio=0.05767
3、短电弧小圆内接正六边形面积As与短电弧小圆Al之比
import math
def calculate_ns(r):
numerator = (3 * math.sqrt(3) / 2) * r * r
denominator = math.pi * r * r
ns = (numerator / denominator) * 100
return ns
results = find_all_n_and_x()
ns = calculate_ns(r)
print(f"ns={ns:.5f}%")ns=82.69933%
二、两种六边形密铺可视化并计算次数
输出多个数据方便后续直接拟合,可修改三引号附近内容,直接定义r=半径数据输出单一图像
1、以大圆圆心为原点
import numpy as np
import matplotlib.pyplot as plt
import math
def hexagon(p, r, theta):
#计算每个顶点的坐标
X = p[0] + r * np.cos(theta)
Y = p[1] + r * np.sin(theta)
plt.plot(X, Y, color='black')
#alpha透明度
plt.fill(X, Y, 'w', alpha=0.3)
#定义calculate_distance函数计算两点之间的距离,输入两个点的坐标
def calculate_distance(x1, y1, x2, y2):
return math.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
R = 1000
#绘制正六边形的角度,六个顶点
theta = np.arange(0, 2 * np.pi, 2 * np.pi / 6)
number_circlecenter=[]
'''修改以下三行,直接定义r=半径数据可输出单一图像'''
r_draw = [i for i in np.arange(55, 80, 0.5)]
for i in np.arange(55,80,0.5):
r=i
#画大圆
theta_out = np.linspace(0, 2*np.pi, 1000)
X = R * np.cos(theta_out)
Y = R * np.sin(theta_out)
fig = plt.figure()
axes = fig.add_subplot()
axes.axis('equal')
plt.plot(X, Y, color='black')
plt.fill(X, Y, 'w', alpha=0.3)
#计算以圆心坐标
x1 = []
y1 = []
n = math.ceil(R / (r * np.sqrt(3)/2))
#遍历大圆计算圆心,存储圆心坐标
for i in range(-n, n+1):
for j in range(-n, n+1):
#两层循环嵌套计算圆心x、y坐标值
#i表示行号,r为六边形边长,即通过每两列之间的水平偏移r*np.sqrt(3)计算x坐标值
x = j * 3 * r / 2
#j表示列号,r表示六边形变长,即通过相邻列在垂直错位3 * r / 2
y = (i+0.5*(j%2)) * r * np.sqrt(3)
#通过取余运算实现奇数列错位排布
#删除超出大圆范围的值
if calculate_distance(x, y, 0, 0) <= R + r:
x1.append(x)
y1.append(y)
#绘制满足条件的正六边形
for i in range(len(x1)):
hexagon([x1[i], y1[i]], r, theta)
#绘制坐标轴
plt.axhline(0, -1111, 1111,color='black')
plt.axvline(0, -1111, 1111,color='black')
print(f"r={r}最少的正六边形数量为:{len(x1)}" )
number_circlecenter.append(len(x1))
plt.show()
2、以正六边形的顶点为原点
基本与前代码一致,主要修改了小圆圆心的位置
import numpy as np
import matplotlib.pyplot as plt
import math
def hexagon(p, r, theta):
#计算每个顶点的坐标
X = p[0] + r * np.cos(theta)
Y = p[1] + r * np.sin(theta)
plt.plot(X, Y, color='black')
#alpha透明度
plt.fill(X, Y, 'w', alpha=0.3)
#定义calculate_distance函数计算两点之间的距离,输入两个点的坐标
def calculate_distance(x1, y1, x2, y2):
return math.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
R = 1000
#绘制正六边形的角度,六个顶点
theta = np.arange(0, 2*np.pi,2*np.pi / 6)
number_sixcenter=[]
r_draw = [i for i in np.arange(55, 80, 0.5)]
for i in np.arange(55,80,0.5):
r=i
#画大圆
theta_out = np.linspace(0, 2*np.pi, 1000)
X = R * np.cos(theta_out)
Y = R * np.sin(theta_out)
fig = plt.figure()
axes = fig.add_subplot()
axes.axis('equal')
plt.plot(X, Y, color='black')
plt.fill(X, Y, 'w', alpha=0.3)
#计算以圆心坐标
x1 = []
y1 = []
n = math.ceil(R / (r * np.sqrt(3)/2))
#遍历大圆计算圆心,存储圆心坐标
for i in range(-n, n+1):
for j in range(-n, n+1):
#两层循环嵌套计算圆心x、y坐标值
x = j * 3 * r / 2+r*math.sqrt(3)/2
#j表示列号,r表示六边形变长,即通过相邻列在垂直错位3 * r / 2
y = (i+0.5*(j%2)) * r * np.sqrt(3)
#删除超出大圆范围的值
if calculate_distance(x, y, 0, 0) <= R + r:
x1.append(x)
y1.append(y)
#绘制满足条件的正六边形
for i in range(len(x1)):
hexagon([x1[i], y1[i]], r, theta)
#绘制坐标轴
plt.axhline(0, -1111, 1111,color='black')
plt.axvline(0, -1111, 1111,color='black')
print(f"r={r}最少的正六边形数量为:{len(x1)}")
number_sixcenter.append(len(x1))
plt.show()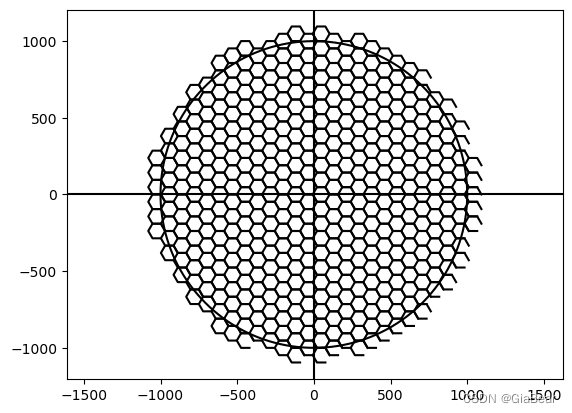
三、数据拟合
1、存储输出dataframe数据
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame.from_dict(
{'r': r_draw, 'number_circlecenter':number_circlecenter,'number_sixcenter': number_sixcenter})
df.head(50)
2、多项式拟合
import matplotlib.pyplot as plt
import numpy as np
x = r_draw
'''修改y值输出两种方式的拟合结果'''
y = np.array(number_circlecenter)
z1 = np.polyfit(x, y, 4) # 用4次多项式拟合
p1 = np.poly1d(z1)
print(p1) # 在屏幕上打印拟合多项式
yvals=p1(x) # 也可以使用yvals=np.polyval(z1,x)
plot1=plt.plot(x, y, '*',label='original values')
plot2=plt.plot(x, yvals, 'r',label='polyfit values')
plt.xlabel('r')
plt.ylabel('count')
plt.legend(loc=1) # 指定legend的位置
plt.title('circlecenter')
plt.show()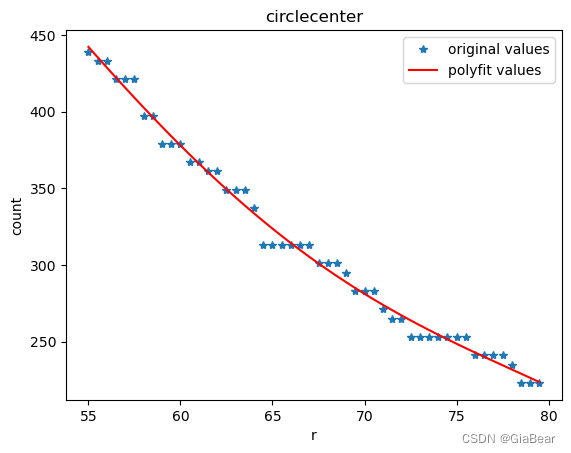
























 1156
1156

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








