前言
图论,说白了就是在一张图上进行各种操作,包括简单的如求最短路,难的如强连通分量。本文将带你走入图论,了解图论的基础知识与图上最短路问题。
图论基础
图论其实没什么太多底层的知识,如果真有那就只能是图的存储了。
每一道题我们都需要找到一个合适的存图方式,今天我就在这里讲一讲图的三种基本存储方式。
1. 邻接矩阵
邻接矩阵是最直观且最浪费空间的一种存储方式,它大致就是定义一个数组 g[N][N],其中 g[i][j] 的值表示
i
i
i 到
j
j
j 有没有路。所以说这个 g[N][N] 其实是一个布尔类型的数组。(你想定义成 int 也行。)
但是光是 g 一个数组就占了
O
(
N
2
)
O(N^2)
O(N2) 的空间复杂度,实在太高,一般不建议使用这个。
2. 链式前向星
聪明的计算机学家们就又想出了一个办法:按照链表的方式存图。
因为我们不需要把所有的任意两个点之间的关系都描述一遍,只需要看看每个点与那些点连在一起就行。于是,我们只需要定义一个结构体数组 g[N],存储这个点里面有哪些点与之相连,因为是一个链表,所以还要多存储一个下一个位置在几号。
链式前向星的原代码是用指针完成的,但是由于指针过分难写,现在一般都改成这种样子:
struct edge{
int ed,nx;
}g[N];
int cnt,head[N];
void add(int st,int ed)//连边
{
g[++cnt].ed=ed;
g[cnt].nx=head[st];
head[st]=cnt;
}
但是这种写法过分难以理解,对于许多初学者来说很不友好。
3. 邻接表
在 STL 被发明以后,计算机学家们看中了一个 STL:vector。这个 STL 具有自动延长空间的性质,在你不需要时不会多借一点内存,很省空间,于是计算机学家们就发明了第三种存图方式:邻接表。
大致原理是这样的:定义一个 vector<int>g[N];,其中 g[i] 内的元素都是与 i 相连边的点,这种写法清晰、直观,是很多初学者常用的存图方式。
具体代码如下:
vector<int>g[N];
int main()
{
cin>>n;//n 条边
for(int i=1,x,y;i<=n;i++){
cin>>x>>y;
g[x].emplace_back(y);//x 与 y 相连
g[y].emplace_back(x);//y 与 x 相连
}
}
注:这里我建的是双向边,如果要建单向边,只需要其中一个就行了。
最短路
存图方法介绍完了,该讲讲最短路了。
1. Floyd
Floyd 算法是所有最短路中最暴力、时间复杂度最高的算法,它主要是类似于 DP 的思想:对于从 i i i 到 j j j 的问题,有两种情况:
- i → j i\to j i→j
- i → k → j i\to k\to j i→k→j
如下图:

其中红色路径是一种,黑色路径是一种,然后看看哪种最短就行了。
代码也是非常的粗暴:
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
for(int k=1;k<=n;k++)
{
if(i!=j&&j!=k)//大前提(很好奇怎么从自己走向自己)
{
dis[i][j]=min(dis[i][j],dis[i][k]+dis[j][k]);
}
}
}
}
其中,dis[i][j] 表示从
i
i
i 到
j
j
j 的最短距离(英文单词:distance,中文意思:距离),这种算法很好理解,但时间复杂度也很高,一眼就能看出是
O
(
n
3
)
O(n^3)
O(n3)。
2. Bellman-Ford
为了能够解决数据更大的最短路问题,聪明的计算机学家们又发明了 Bellman-Ford(贝尔曼-福特)算法。(为了不累死作者,后面一律把 Bellman-Ford 简写为 BF。)
BF 算法其实有个很好玩的现实对应:问路。
假设一个路人在 i i i 号点,他问 i i i 号点的人: j j j 号点怎么走最短。 i i i 不知道,但他会问他相邻的点上的人,直到问到了 j j j 号点的人, j j j 号点的人又再把信息传回去。
所以 BF 算法的步骤就如下:
- 找到一条边的起点 s t st st 与终点 e d ed ed。
- 看看通过 s t st st 到 j j j 的距离是否比当前从 e d ed ed 到 j j j 的距离短,如果是,更新距离。
- 重复执行上述操作 n n n 次。
这里稍微用到了一下抽屉原理,因为抽屉原理告诉我们:按照前两步操作执行 n n n 次就一定能找到最短路。
算一下时间复杂度:一共进行 n n n 轮,每一轮遍历了 m m m 条边,时间复杂度: O ( n m ) O(nm) O(nm)。
代码如下:
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(dis[g[j].st]>dis[g[j].ed]+g[j].s) dis[g[j].st]=dis[g[j].ed]+g[j].s;
}
}
(别小看这五行代码,它可是起到了大作用的。)
所以从上述定义来看,BF 算法好像只能解决单源最短路问题(即探究从一个固定的点到另一个其他点的最短路),而 Floyd 则可以解决任意两点之间的最短路问题。
但是,计算机学家们又发现了个新问题:有时候在跑完最短路之后发现居然能跑出比最短路还短的路。这就是负环独有的特性。对于负环的处理,计算机学家们决定采用再跑一次的策略,如果还能找到最短路,那就肯定是负环了。
3. SPFA
可贪心的计算机学家们还是认为不够啊,他们想把时间复杂度压到更低。终于,在 1994 年,来自我国西南交大的段凡丁老师提出了一种全新的算法:SPFA(Shortest Path Faster Algorithm)。在他的证明中,SPFA 可以把时间复杂度降到 O ( n ) O(n) O(n),即把每个点遍历一遍就行。但是因为他的证明有误,所以 SPFA 实际上在最坏情况下时间复杂度是和 BF 一样的。
但是 SPFA 的失败却带来了意外的成功,因为它在最好情况下可以达到 O ( n ) O(n) O(n) 的时间复杂度,而且它可以判负环,所以直到现在很多信竞生仍在使用它。
SPFA 的原理其实就是用队列优化了一下 BF,具体操作如下:
- 把起点入队。
- 让队列中的第一个点出队,更新与之相邻的点。
- 如果某个点能被更新且不再队列里,把这个点推入队列。
- 重复执行上述操作,直到队列为空。
SPFA 算法很巧妙地把一些没用的计算给扔掉,而保留了重要的部分,这也是为什么它能如此——不稳定了。
代码如下:
vector<pair<int,int>>g[N];//pair<当前点到达的终点,当前两点间的距离>
void SPFA(int st)
{
memset(dis,0x3f,sizeof(dis));//最短路
memset(inq,0,sizeof(inq));//是否在队列里(in queue)
memset(num,0,sizeof(num));//每个点被遍历的次数
//如果某个点被遍历了超过 n 次,那就有负环,这一点与 BF 是一致的
inq[st]=1;
dis[st]=0;
queue<int>q;
q.push(st);
while(!q.empty()){
int x=q.front();
q.pop();
inq[x]=0;
if(num[x]>n){//有负环
cout<<"-1";
return;
}
for(auto i:g[x]){
if(dis[i.first]>dis[x]+i.second){
dis[i.first]=dis[x]+i.second;
if(!inq[i.first]){
q.push(i.first);
inq[i.first]=1;
num[i.first]++;
}
}
}
}
}
SPFA 已死?

SPFA 的不稳定性,一直是许多 OIer 的心头之痛,每一次写 SPFA 就像是在赌运气一样,这使得 SPFA 成了“能不用,就不用”的一种“小算法”。可,SPFA 的失败不也带来了意外之喜吗?我们有了除 BF 之外的其他时间复杂度更低、能判负环的算法,所以还是请大家好好珍惜 SPFA 吧。
4. Dijkstra
在 STL 被发明过后,计算机学家们便找到了一种更高效、简单的算法:Dijkstra!(为了不被累死,后面都使用 Dij 来代指 Dijkstra。)
Dij 的本质就是一个加了贪心的 BFS,大致过程如下:
- 把起点推入优先队列里。
- 取出优先队列里的第一个点,如果这个点已经被遍历过,那么就直接跳过,否则更新它周围的点。
- 如果某个点能被更新且没有被遍历过,把当前点推入优先队列。
- 重复执行上述操作直到优先队列为空。
这个原因也很简单:我们通过优先队列排序会找到当前离起点最近的点,那么这个点就已经找到它的最短路了,如果还有其他点想要来更新它,那它使一定不会变的,所以可以直接跳过。
代码如下:
vector<pair<int,int>>g[N];
void dijkstra(int st)
{
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq;//小根堆,按照 pair 的第二个元素排序
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[st]=0;
pq.push(make_pair(st,dis[st]));
while(!pq.empty()){
pair<int,int>p=pq.top();
pq.pop();
int u=p.first;
if(vis[u]){//已经求到最小值了
continue;
}
vis[u]=1;
for(auto i:g[u]){
if(vis[i.first]){//邻居已经找到最小值了
continue;
}
if(dis[i.first]>dis[u]+i.second){
dis[i.first]=dis[u]+i.second;
pq.push(make_pair(i.first,dis[i.first]));//优先队列里面会自动排好序,计算 dis 最小的
}
}
}
}
这种算法的时间复杂度只有 O ( m log 2 ( n ) ) O(m\log_2(n)) O(mlog2(n)),非常的优秀。
可惜,这种优秀的算法有个极大地缺点:不能跑有负边权的图。因为 BFS 是一个逐渐向外扩散的过程,有可能你给你邻居算的最短路并不是最短路,可能在经过一些负边权后得到了一条更短的路,但由于 BFS 的局限性,这种算法一开始就会认定第一次的最短路就是最短的,而不会更新真正的最短值。
如果还不懂,可以输入下面样例:
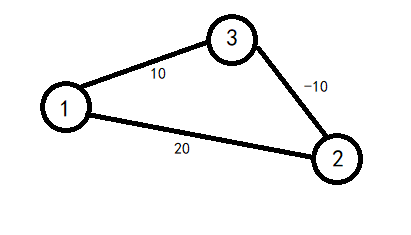
输入格式: 第一行两个数 n n n 和 m m m,表示有 n n n 个点、 m m m 条边。第 2 2 2 至 m + 1 m+1 m+1 行,每行三个数 x , y , s x,y,s x,y,s,表示起点、终点、两点间的边长。注意,这是个双向图。
输出格式: 输出仅一行,表示从 1 1 1 到 n n n 的最短距离。
3 3
1 3 10
1 2 20
2 3 -20
不会敲代码的小白可以看这张图按照上述流程模拟一下:
结语
再伟大的算法,都有自己的缺陷;再完美的人,都有自己的弱点。有时候,表面上的失败可能会有意外的成功,拼运气的随机也有着底层的逻辑。或许,几千年后 OIer 在回看这 OI 界时,会不会有些许感慨,又会不会有些许享受?有时候,完美不一定是无瑕,失败不一定是不成功,随机不一定是赌运气。所以还是请大家享受随机、享受成功的失败吧。


























 237
237

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








