【算法基础11】最短路问题汇总（dijkstra,bellman-ford,SPFA,floyd）

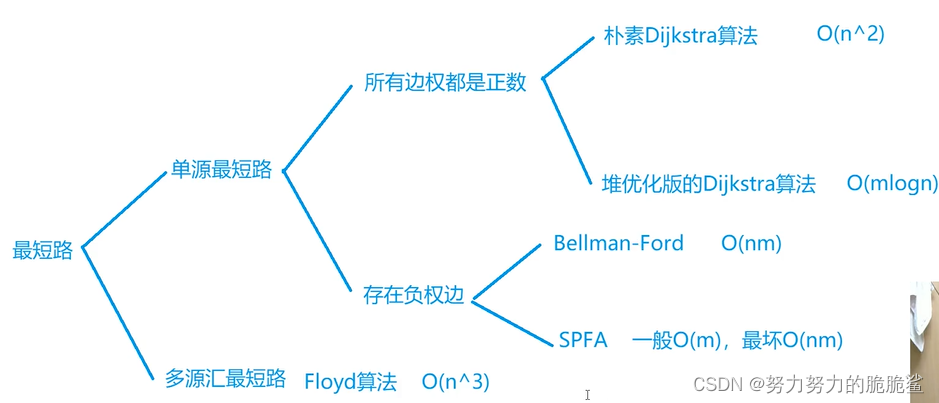
 一、单源正权边——dijkstra

        主要思想：由三点之间的最短路实现找到全图最短路。起始点为题目要求的单源，定义数组dist[]存储图中其他点到起始点的最短路，中间点t为还没有确定最短路（即st[]为false）的点中距离起始点最近的点，终点j为与中间点有边的所有点。依次遍历这些点，如果从起始点经过中间点再到终点的距离小于从起始点到终点的距离，那么就以这段距离更新最短路，即更新dist[j]。与中间点相邻的所有点都遍历完后，将中间点的st[t]更改为true，即t结点已经找到了最短路径，完成了它的使命，不再参与后面的遍历。不断循环，最终所有点的最短路都能确定。

        例题：给出n个结点，m条边组成的图，m行数据每行代表边的起点a,边的终点b,边的权重c，找出从起点到终点的最短路径长度，如果不存在则输出-1。

        ①稠密数据——朴素dijkstra：用邻接矩阵存储图

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010;

int n,m;
int g[N][N],dist[N];
bool st[N];

int dijkstra(){
	memset(dist,0x3f,sizeof(dist));
	dist[1]=0;//最短路初始化
	
	for(int i=0;i<n;i++){
		int t=-1;
		for(int j=1;j<=n;j++){//寻找距离起点最近的中间点t
			if(!st[j]&&(t==-1||dist[t]>dist[j]))
				t=j;
		}
		
		for(int j=1;j<=n;j++)
			dist[j]=min(dist[j],dist[t]+g[t][j]);//更新终点的最短路
    
        st[t]=true;//标记t已经当过中间点了
	}
	
	if(dist[n]==0x3f3f3f3f) return -1;//不存在最短路
	else return dist[n];
}
int main(){
	scanf("%d %d",&n,&m);
	memset(g,0x3f,sizeof(g));

	while(m--){
		int a,b,c;
		scanf("%d %d %d",&a,&b,&c);
		g[a][b]=min(g[a][b],c);//处理自环、重边情况
	}

	cout<<dijkstra()<<endl;
}

        ②稀疏数据——堆优化dijkstra：用邻接表存储图

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1010;

typedef pair<int,int> PII;
int n,m,idx=0;
int h[N],e[N],ne[N],w[N],dist[N];//新增w[]存储边的权重
bool st[N];

void add(int a,int b,int c){//插入边
	e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

int dijkstra(){
	memset(dist,0x3f,sizeof(dist));
	dist[1]=0;
	
	priority_queue<PII,vector<PII>,greater<PII>> heap;//用优先队列构建小端堆
	heap.push({0,1});//存入起点
	
	while(heap.size()){
		auto t=heap.top();//堆顶即为距离最短的中间点t
		heap.pop();

		int ver=t.second,distance=t.first;
		if(st[ver]) continue;//处理重边情况
		
		for(int i=h[ver];i!=-1;i=ne[i]){//沿着邻接表遍历邻接边
			int j=e[i];
			if(dist[j]>distance+w[i]){//更新最短路
				dist[j]=distance+w[i];				
				heap.push({dist[j],j});
			}
		}
		st[ver]=true;//标记t已经当过中间点
	}
	
	if(dist[n]==0x3f3f3f3f) return -1;
	return dist[n];
}
int main(){
	scanf("%d %d",&n,&m);
	memset(h,-1,sizeof(h));

	while(m--){
		int a,b,c;
		scanf("%d %d %d",&a,&b,&c);
		add(a,b,c);
	}
	cout<<dijkstra()<<endl;
}

二、单源负权边——bellman_ford和SPFA

        主要思想：

        bellman_ford：遍历每条边，如果从路径单源到边的终点的距离小于从路径单源到边的起点的距离加上边的权重，则更新从路径单源到边的终点的距离。当限定最短路径经过的边的条数时，可以保证不会陷入负权环死循环的情况。

        SPFA：在bellman_ford的基础上减少不必要的搜索以提高效率。用一个队列存储更新过的结点，每次只遍历以队列中结点为起点的边。可以引入数组cnt[]记录最短路径经过的边的条数，如果cnt>=n，则一定有结点经过了多次，存在负权边。

        例题：给出n个点，m条边组成的图，限定路径边数不超过k，求从图的起点到终点的最短距离，如果不存在则输出“impossible”。

        ①bellman_ford

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010,M=51;

int n,m,k;
int dist[N],backup[N];//backup为上一次更新的dist的备份

struct edg{
	int a,b,w;
}edges[M];

int bellman_ford(){
	memset(dist,0x3f,sizeof(dist));
	dist[1]=0;

	for(int i=0;i<k;i++){//限定k条边则迭代k次
		memcpy(backup,dist,sizeof(dist));//对dist进行备份保证每次只更新一个点的距离
		for(int j=0;j<m;j++){
			int a=edges[j].a,b=edges[j].b,w=edges[j].w;
			dist[b]=min(dist[b],backup[a]+w);
		}
	}
	return dist[n];
} 
int main(){
	scanf("%d %d %d",&n,&m,&k);

	for(int i=0;i<m;i++){
		int a,b,w;
		scanf("%d %d %d",&a,&b,&w);
		edges[i].a=a,edges[i].b=b,edges[i].w=w;
	}

	int ans=bellman_ford();
	if(ans>0x3f3f3f3f/2) printf("impossible\n");
	else printf("%d\n",ans);
	return 0;
}

     

        ②SPFA

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1010;

int n,m,idx=0;
int h[N],e[N],ne[N],w[N],dist[N],cnt[N]={0};//cnt[]存储经过边的条数
bool st[N];

void add(int a,int b,int c){
	e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

int spfa(){
	memset(dist,0x3f,sizeof(dist));
	dist[1]=0;
	
	queue<int> q;//构建队列存储更新过的结点
	q.push(1);
	st[1]=true;
	
	while(q.size()){
		int t=q.front();
		q.pop();
		st[t]=false;//st表示该结点是否在队列内，防止一个结点在队列内出现多次
		
		for(int i=h[t];i!=-1;i=ne[i]){
			int j=e[i];
			if(dist[j]>dist[t]+w[i]){
				dist[j]=dist[t]+w[i];
				cnt[j]=cnt[t]+1;

				if(cnt[j]>=n) printf("有负环\n");
				if(!st[j]){//更新过且不在队列内的结点进队
					q.push(j);
					st[j]=true;	
				}
			}
		}
	}
	
	if(dist[n]==0x3f3f3f3f) return -1;
	return dist[n];
}
int main(){
	scanf("%d %d",&n,&m);
	memset(h,-1,sizeof(h));

	while(m--){
		int a,b,c;
		scanf("%d %d %d",&a,&b,&c);
		add(a,b,c);
	}

	int ans=spfa();
	if(ans>0x3f3f3f3f/2) printf("impossible\n");
	else printf("%d\n",ans);
}

三、多源负权——floyd

        主要思想：通过三层循环更新全图的最短路。其中第一层循环的k代表中间结点，第二层循环的i代表起点，第三层循环的j代表终点。用邻接矩阵存储图，且直接在邻接矩阵中更新最短路。

        例题：给出n个点，m条边组成的图。有q个询问，每次输出从结点a到结点b的最短路径，如果不存在则输出“impossible”。

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010,INF=1e9;

int n,m,q;
int g[N][N];

int floyd(){
	for(int k=1;k<=n;k++){//中间结点
		for(int i=1;i<=n;i++){//起点
			for(int j=1;j<=n;j++)//终点
				g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
		}
	}
}
int main(){
	scanf("%d %d %dq",&n,&m,&q);
	for(int i=1;i<=n;i++){
		for(int j=0;j<=n;j++){
			if(i==j) g[i][j]=0;//消除自环情况
			else g[i][j]=INF;
		}
	}

	while(m--){
		int a,b,c;
		scanf("%d %d %d",&a,&b,&c);
		g[a][b]=min(g[a][b],c);
	}

	floyd();

	while(q--){
		int a,b;
		scanf("%d %d",&a,&b);
		if(g[a][b]>INF/2) printf("impossible\n");
		else printf("%d\n",g[a][b]);
	}
	return 0;
}